初中数学苏科版九下 利用辅助圆求解动点最值问题 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版九下 利用辅助圆求解动点最值问题 教学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 455.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览

文档简介
利用辅助圆求解动点最值问题
许多几何问题虽然与圆无关,但是如果能结合条件补作辅助圆,就能利用圆的有关性质、结论,将某些最值问题通过圆中的几何模型求解.笔者经过研究,归纳为以下情况可考虑作辅助圆:
一、同一端点出发的等长线段
例1
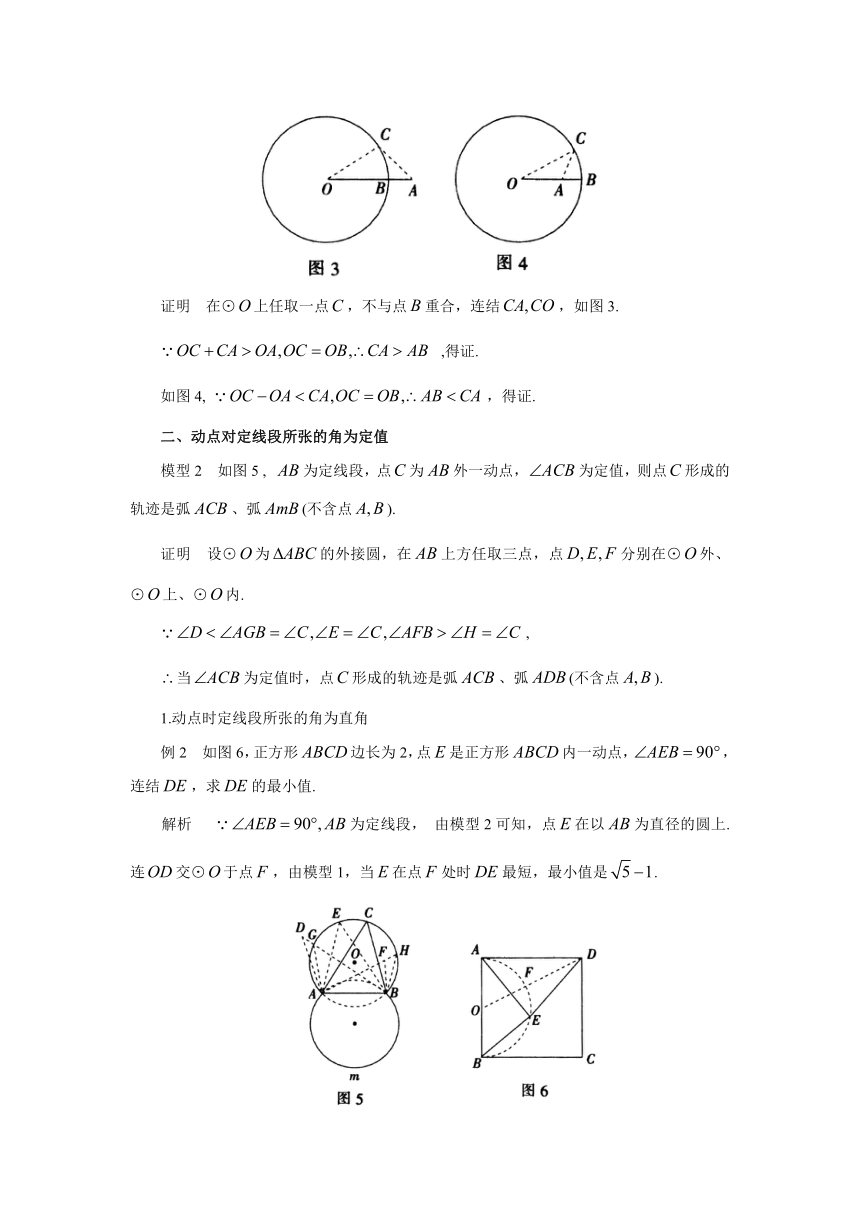
如图1,在直角梯形中,
,点是线段上一动点,将沿翻折到,连结.当点在上运动时,分别求的最小值.
解析
如图1,当点在点时,与重合;当点在点时,设点在点处,由翻折可知.所以,点在以为圆心,为半径的圆上,运动轨迹为弧.
如图2,点在⊙内,延长交⊙于点.当点在点时最小,最小值为.
点在⊙外,设交⊙于点,当点在点时最小,最小值为.
设与⊙交点为,当点在点时最小,最小值为.
点评
当条件中有同一端点出发的等长线段时,根据圆的定义,以该端点为圆心,等长为半径构造圆,将原问题转化为定点与圆上点的距离问题.
模型1
如图3,点在⊙外,到⊙上各点连线段中最短;如图4,点在⊙内,到⊙上各点连线段中最短.
证明
在⊙上任取一点,不与点重合,连结,如图3.
,得证.
如图4,
,得证.
二、动点对定线段所张的角为定值
模型2
如图5
,
为定线段,点为外一动点,为定值,则点形成的轨迹是弧、弧(不含点).
证明
设⊙为的外接圆,在上方任取三点,点分别在⊙外、⊙上、⊙内.
,
当为定值时,点形成的轨迹是弧、弧(不含点).
1.动点时定线段所张的角为直角
例2
如图6,正方形边长为2,点是正方形内一动点,,连结,求的最小值.
解析
为定线段,
由模型2可知,点在以为直径的圆上.连交⊙于点,由模型1,当在点处时最短,最小值是.
点评
当动点对定线段所张的角为直角时,根据直径所对圆周角为直角,以定线段为直径构造圆.
2.动点时定线段所张的角为锐角
例3
如图7,
,一把直角三角形尺的两个顶点分别在上移动,,求点到距离的最大值.
解析
如图8,⊙为的外接圆,由模型2知,点的运动轨迹是弧(两点除外).过点作的垂线,垂足为点,交弧于点,当点在点处时,到
的距离最大,即为长.
.
,
.
故到距离的最大值为.
点评
本题是定长,为定值,利用模型2,找到点的运动轨迹是一段弧,
这段弧所在的圆是一个定圆,于是原问题转化为圆上一点到弦的距离问题.
模型3
如图9,是⊙的一条弦,点是⊙上一动点(不与重合),过点作
,垂足为,交⊙于点在两侧).当点在点处时,点到的距离最大,即为长.
证明
如图9,作垂足为点,,得证.
3.动点对定线段所张的角为钝角
例4
如图10,正三角形边长为2,射线,点是射线上一动点(不与点重合),外接圆交于点,求的最小值.
解析
如图10
,
.
为定长,点的运动轨迹是弧(不与重合).
过点作垂足为,交弧于点,当点在点时最小,最小值为.
点评
本题将动点转化到动点,且因为,为定长,由模型2可知,点的运动轨迹是弧,这段弧所在的圆是一个定圆.于是,的最小值问题转化为圆外一点到圆上一点的最小值问题,由模型1即可求解.
三、动点对定线段所张的角的最值
例5
如图11,四边形中,均有
.在边上,是否存在一点,使得的值最小 若存在,求出此时的值;若不存在,请说明理由.
解析
当为锐角时,随的增大而减小,求的值最小值,只要求最大值.
于是,作中垂线交于点.设三点确定⊙,则⊙切于点.此时上的点(除点)都在⊙外,,所以当点在点处时最大.
由题意,可知.
设⊙半径为,
则,
解得,,
所以最小值为.
点评
求动点对定线段所张角的最大值时,以定线段为弦所作的圆与动点所在的直线相切,由同弧所对的圆周角大于圆外角知,动点运动至切点处时所张角最大.
许多几何问题虽然与圆无关,但是如果能结合条件补作辅助圆,就能利用圆的有关性质、结论,将某些最值问题通过圆中的几何模型求解.笔者经过研究,归纳为以下情况可考虑作辅助圆:
一、同一端点出发的等长线段
例1
如图1,在直角梯形中,
,点是线段上一动点,将沿翻折到,连结.当点在上运动时,分别求的最小值.
解析
如图1,当点在点时,与重合;当点在点时,设点在点处,由翻折可知.所以,点在以为圆心,为半径的圆上,运动轨迹为弧.
如图2,点在⊙内,延长交⊙于点.当点在点时最小,最小值为.
点在⊙外,设交⊙于点,当点在点时最小,最小值为.
设与⊙交点为,当点在点时最小,最小值为.
点评
当条件中有同一端点出发的等长线段时,根据圆的定义,以该端点为圆心,等长为半径构造圆,将原问题转化为定点与圆上点的距离问题.
模型1
如图3,点在⊙外,到⊙上各点连线段中最短;如图4,点在⊙内,到⊙上各点连线段中最短.
证明
在⊙上任取一点,不与点重合,连结,如图3.
,得证.
如图4,
,得证.
二、动点对定线段所张的角为定值
模型2
如图5
,
为定线段,点为外一动点,为定值,则点形成的轨迹是弧、弧(不含点).
证明
设⊙为的外接圆,在上方任取三点,点分别在⊙外、⊙上、⊙内.
,
当为定值时,点形成的轨迹是弧、弧(不含点).
1.动点时定线段所张的角为直角
例2
如图6,正方形边长为2,点是正方形内一动点,,连结,求的最小值.
解析
为定线段,
由模型2可知,点在以为直径的圆上.连交⊙于点,由模型1,当在点处时最短,最小值是.
点评
当动点对定线段所张的角为直角时,根据直径所对圆周角为直角,以定线段为直径构造圆.
2.动点时定线段所张的角为锐角
例3
如图7,
,一把直角三角形尺的两个顶点分别在上移动,,求点到距离的最大值.
解析
如图8,⊙为的外接圆,由模型2知,点的运动轨迹是弧(两点除外).过点作的垂线,垂足为点,交弧于点,当点在点处时,到
的距离最大,即为长.
.
,
.
故到距离的最大值为.
点评
本题是定长,为定值,利用模型2,找到点的运动轨迹是一段弧,
这段弧所在的圆是一个定圆,于是原问题转化为圆上一点到弦的距离问题.
模型3
如图9,是⊙的一条弦,点是⊙上一动点(不与重合),过点作
,垂足为,交⊙于点在两侧).当点在点处时,点到的距离最大,即为长.
证明
如图9,作垂足为点,,得证.
3.动点对定线段所张的角为钝角
例4
如图10,正三角形边长为2,射线,点是射线上一动点(不与点重合),外接圆交于点,求的最小值.
解析
如图10
,
.
为定长,点的运动轨迹是弧(不与重合).
过点作垂足为,交弧于点,当点在点时最小,最小值为.
点评
本题将动点转化到动点,且因为,为定长,由模型2可知,点的运动轨迹是弧,这段弧所在的圆是一个定圆.于是,的最小值问题转化为圆外一点到圆上一点的最小值问题,由模型1即可求解.
三、动点对定线段所张的角的最值
例5
如图11,四边形中,均有
.在边上,是否存在一点,使得的值最小 若存在,求出此时的值;若不存在,请说明理由.
解析
当为锐角时,随的增大而减小,求的值最小值,只要求最大值.
于是,作中垂线交于点.设三点确定⊙,则⊙切于点.此时上的点(除点)都在⊙外,,所以当点在点处时最大.
由题意,可知.
设⊙半径为,
则,
解得,,
所以最小值为.
点评
求动点对定线段所张角的最大值时,以定线段为弦所作的圆与动点所在的直线相切,由同弧所对的圆周角大于圆外角知,动点运动至切点处时所张角最大.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
