2017年中考数学苏科版压轴题专题 求三角形面积最大值 教学案(含答案)
文档属性
| 名称 | 2017年中考数学苏科版压轴题专题 求三角形面积最大值 教学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 523.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-17 11:20:39 | ||
图片预览



文档简介
求三角形面积最大值
在中考压轴题中有一类题目是函数综合题,其中有一问涉及了三角形的面积的最值问题.这类题通常会涉及到一个动点,问这个动点运动到什么位置的时候面积最大.对于这类题我们可以先用代数式表示此三角形的面积,表示三角形的面积的时候可以采用构底造高法来求,下面呢我们通过一道例题还讲解一下。
一、构底造高法
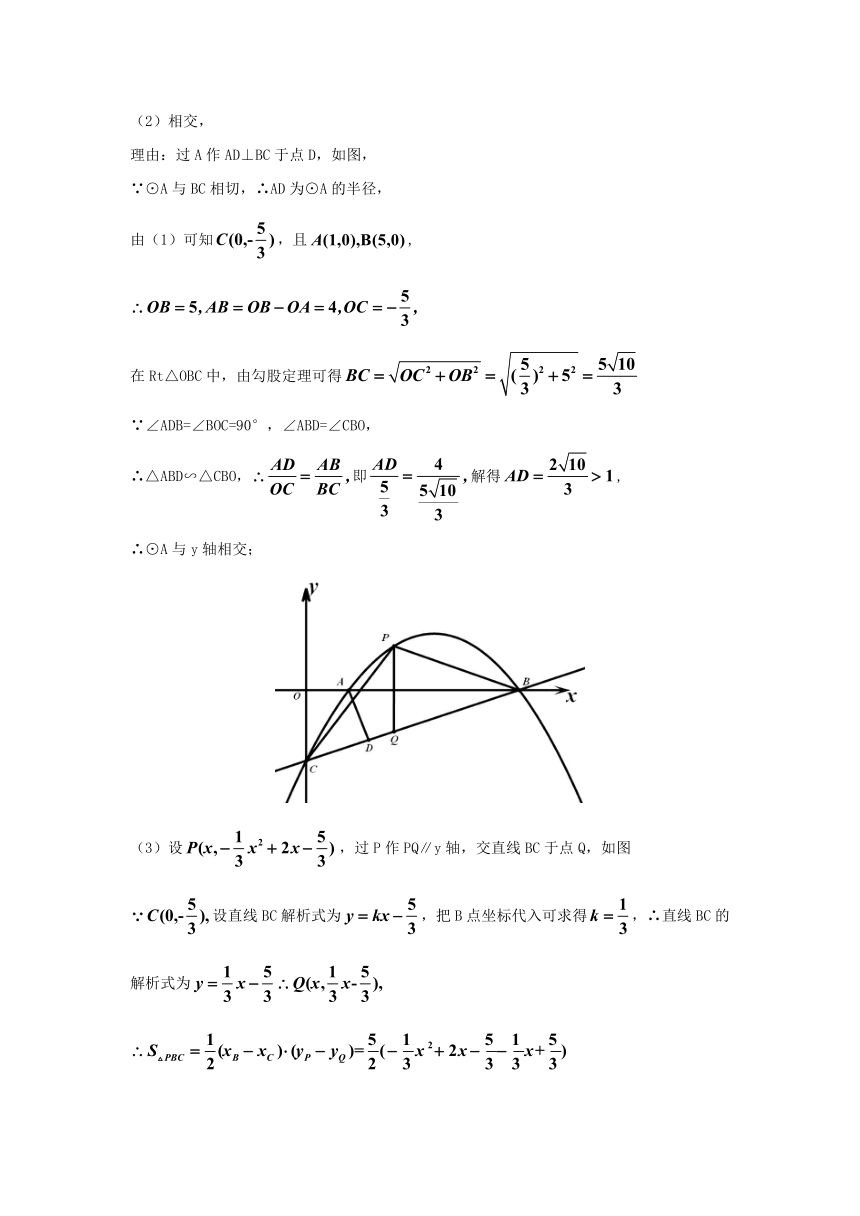
【典例探究】(2016 绥化)如图,抛物线经过点A(1,0)和点B(5,0),与y轴交于点C.
(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.
【思路分析】
(3)过P作PQ∥y轴,交直线BC于点Q,P、Q两点的横坐标相同,则可推导出
【解答】解:(1)∵抛物线经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得解得
∴抛物线解析式为
(2)相交,
理由:过A作AD⊥BC于点D,如图,
∵⊙A与BC相切,∴AD为⊙A的半径,
由(1)可知,且,
在Rt△OBC中,由勾股定理可得
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,即解得,
∴⊙A与y轴相交;
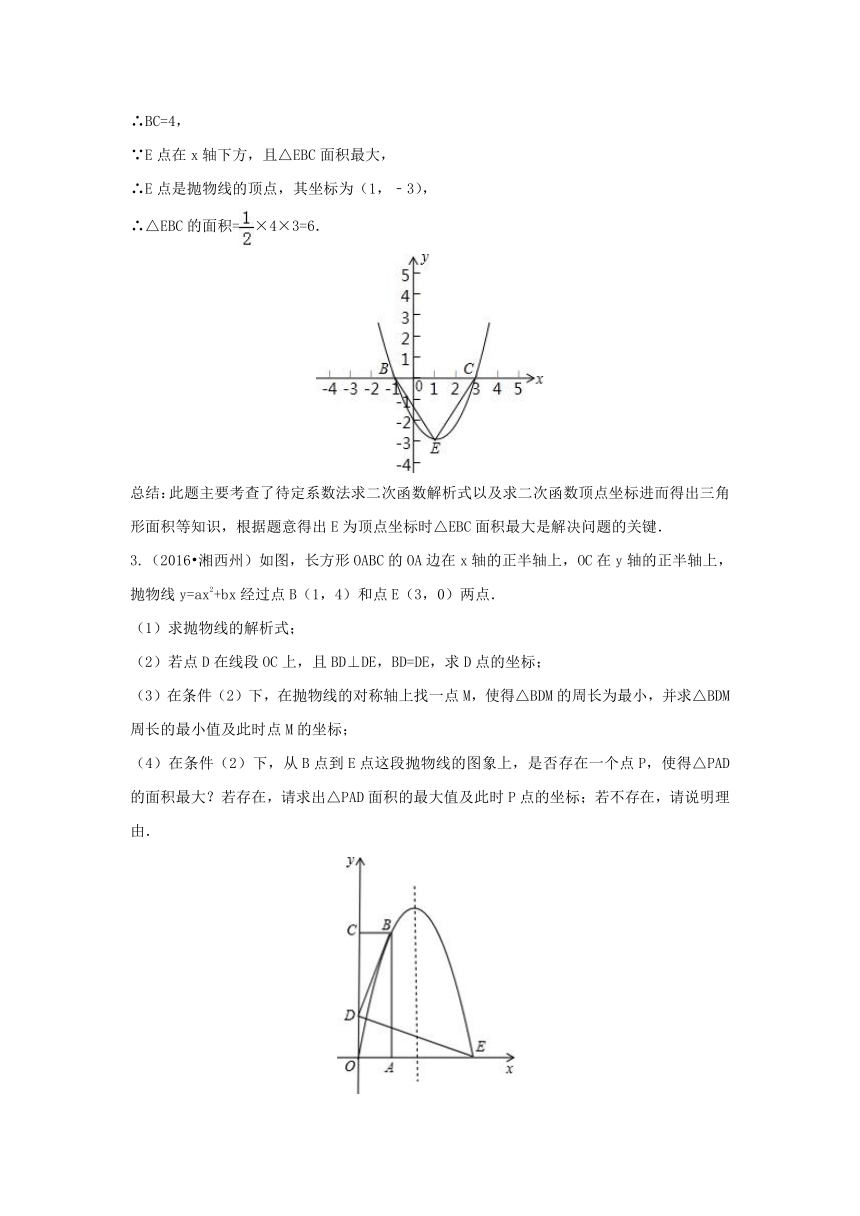
(3)设,过P作PQ∥y轴,交直线BC于点Q,如图
设直线BC解析式为,把B点坐标代入可求得,∴直线BC的解析式为
,
当时,S△PBC有最大值,点P的坐标为
(本题节选自2016年绥化中考)
【方法突破】
所谓“构底造高法”就是重新构造三角形的底或高,使之能直接利用三角形的面积公式求解.通常构造三角形的底或高的方法是过三角形的一个顶点作x轴或y轴的垂线,与三角形的一条固定边相交,从而确定“底”或“高”。
如下图
过点C作CD∥y轴,则
【学以致用】
1.如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于P、与直线BC相交于点M,连接PB.
(1)求抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大 若存在,求出D点坐标及△BCD面积最大值;若不存在,请说明理由.
(3)在(1)中的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等 若存在,求出点Q的坐
标;若不存在,请说明理由.
2.(2011 齐齐哈尔)已知:二次函数y=x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣).
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=﹣.
【分析】(1)利用待定系数法将直线x=1,且经过点(2,﹣)代入二次函数解析式,求二次函数解析式即可;
(2)利用二次函数与x轴相交即y=0,求出即可,再利用E点在x轴下方,且E为顶点坐标时△EBC面积最大,求出即可.
【解答】解:(1)由已知条件得,
解得b=﹣,c=﹣,
∴此二次函数的解析式为y=x2﹣x﹣;
(2)令x2﹣x﹣=0,
∴x1=﹣1,x2=3,
∴B(﹣1,0),C(3,0),
∴BC=4,
∵E点在x轴下方,且△EBC面积最大,
∴E点是抛物线的顶点,其坐标为(1,﹣3),
∴△EBC的面积=×4×3=6.
总结:此题主要考查了待定系数法求二次函数解析式以及求二次函数顶点坐标进而得出三角形面积等知识,根据题意得出E为顶点坐标时△EBC面积最大是解决问题的关键.
3.(2016 湘西州)如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
【答案】解:(1)将点B(1,4),E(3,0)的坐标代入抛物线的解析式得:
解得
抛物线的解析式
(2)∵BD⊥DE,∴∠BDE=90°.∴∠BDC+∠EDO=90°.
又∵∠ODE+∠DEO=90°,∴∠BDC=∠DEO.
在△BDC和△DOE中,∴△BDC≌△DEO.
∴OD=AO=1.∴D(0,1).
(3)如图所示,作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.
,∴点B′的坐标为(2,4).
∵点B与点B′关于对称,∴MB=B′M.∴DM+MB=DM+MB′.
∴当点D、M、B′在一条直线上时,MD+MB有最小值(即△BMD的周长有最小值).
∵由两点间的距离公式可知:,
∴△BDM的最小值为,
设直线B′D的解析式为y=mx+n.
将点D、B′的坐标代入得:解得
∴直线DB′的解析式为
(4)存在.
理由:
如图所示:设点过点P作PG⊥x轴,交直线DA于点G,
∵B(1,4),∴A(1,0),又D(0,1),∴直线AD为,
∴,最大值是
二、平行相切法
【典例探究】
(2015秋 自贡校级月考)如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点,点P是直线BC下方的抛物线上一动点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使MA+MC的值最小,求点M的坐标;
(3)当点P运动到什么位置时,△PBC的面积最大,并求出此时P点的坐标和△PBC的最大面积.
【考点】二次函数综合题.21世纪教育网
【分析】(1)A(﹣1,0),B(5,0),C(0,﹣)代入y=ax2+bx+c,即可得出抛物线的解析式,
(2)点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,则点M就是BC与抛物线对称轴的交点,把B(5,0),C(0,﹣)代入y=kx+b,求出直线BC的解析式,把抛物线对称轴x=2代入即可得到点M的坐标,
(3)过点P作l∥BC,交y轴于Q点,当l与抛物线只有唯一的公共点P时,△PBC的面积最大,联立方程利用△可求出设此时l的解析式,可求出点P的作坐标,作CN⊥l,利用=求出CN,即可得出△PBC的面积.
【解答】解:(1)设抛物线的解析式为y=ax2+bx+c,把A(﹣1,0),B(5,0),C(0,﹣)代入解析式,
得,解得,
所以抛物线的解析式为y=x2﹣2x﹣.
(2)如图1,点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,
则点M就是BC与抛物线对称轴的交点,
∵抛物线的解析式为y=x2﹣2x﹣.
∴抛物线对称轴x=2,
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,﹣)代入得,解得.
∴直线BC的解析式为y=x﹣,
∵M的横坐标为2,
∴点M的坐标为(2,﹣),
(3)过点P作l∥BC,交y轴于Q点,如图2,
∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=x+n,
∴方程有唯一一组解,即x2﹣2x﹣=x+n有相等的实数解,
整理得x2﹣5x﹣5﹣2n=0,△=52﹣4(﹣5﹣2n)=0,解得n=﹣,y=x﹣,
∴此时P点坐标为(,﹣),
∵Q点坐标为(0,﹣),
作CN⊥l,CQ=OQ﹣OC=﹣=,
∵===,
∴CN= =,
∴△PBC的面积=BC CN=××=.
【方法突破】
所谓“平行相切法”就是作三角形一条固定边的平行线且这条平行线与抛物线“相切”,即与抛物线只有一个交点。这样,就会使得以三角形固定边为底的三角形的高达到最大化,从而三角形的面积也就最大。
【学以致用】
1.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:________.
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大 最大面积是多少
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积,若存在,求出P点的坐标;若不存在,请说明理由.
2.(2014秋 古蔺县校级期中)如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.
(1)求抛物线的解析式及点C的坐标;
(2)当点P运动到什么位置时,△PAB的面积最大?最大面积是多少?
(3)当(2)中点P运动到△PAB的面积最大时,x轴上是否存在点D,使△PDB的周长最小?若存在,求出点D的坐标;若不存在.请说明理由.
21世纪教育网
【分析】(1)把A(﹣4,0),B(0,4)代入抛物线y=﹣x2+bx+c,可得出抛物线解析式,当y=0时即可得出点C的坐标.
(2)设y=x+b与抛物线y=﹣x2﹣3x+4只有一个交点时,△PAB的面积最大,利用判别式求出b的值,再联立可得出点P的坐标,过点B作BM⊥PN交PN于点M,利用三角函数求出BM,再利用△PAB的面积公式即可求出答案.
(3)连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.先求出点B′的坐标,再利用坐标求出PB′所在的直线,即可求出与x轴的交点D的坐标.
【解答】解:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,
∴A(﹣4,0),B(0,4)抛物线y=﹣x2+bx+c经过A、B两点,可得,解得,
∴抛物线解析式为y=﹣x2﹣3x+4.
令y=0,得﹣x2﹣3x+4=0,
解得x1=﹣4,x2=1,
∴C(1,0).
(2)如图1,
设y=x+b与抛物线y=﹣x2﹣3x+4只有一个交点时,△PAB的面积最大,
∵由x+b=﹣x2﹣3x+4化简x2+4x+b﹣4只有一个解,得△=16﹣4×(b﹣4)=32﹣4b=0,解得b=8.
∴y=x+8,
∴联立得方程组得,
解得,
∴P(﹣2,6)
过点B作BM⊥PN交PN于点M,
∵BN=ON﹣OB=8﹣4=4,sin∠MNB=,
∴BM=4×=2,
△PAB的面积=AB BM=×4×2=8.
(3)存在.如图2,
连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.
∵点B(0,4),
∴点B′(0,﹣4),
∵P(﹣2,6)
∴设PB′所在的直线为y=kx+b得,
解得
∴PB′所在的直线为y=﹣5x﹣4,
点D的坐标为(﹣,0).
【点评】本题主要考查了二次函数图象与其他函数图象相结合问题,解题的关键是根据一次函数系数与图象的位置关系判断出图象特征.
三、面积分割法
【典例探究】
如图,已知抛物线与直线y=x交于点A、B两点,A、B的横坐标分别为-1和4.
(1)求此抛物线的解析式.
(2)若平行于y轴的直线x=m()与抛物线交于点M,与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示).
(3)在(2)的条件下,连接OM、BM,是否存在m的值,使得△BOM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
分析:(1)由于A、B两点是抛物线与直线的交点,说明这两点既在直线上又在抛物线上,将两点横坐标代入直线解析式,得到这两点的坐标,再将亮点坐标代入抛物线解析式可得。(2)先根据条件确定N点坐标,用含有m的代数式表示出MP和NP的长度,则不难表示出MN的长度。(3)由于m值不固定,导致△BOM的形状也是动态的,不能直接利用三角形面积公式表示出来,因此我们将△BOM的面积分割成△MON和△BNM两个三角形面积之和。
解:(1)由题意知A(-1,-1),B(4,4),代入y=ax
2+bx-4,得
,
.
∴所求抛物线的解析式为y=x
2-2x-4
(2)由x=m和y=x,得交点N(m,m)
同理可得M(m,m
2-2m-4),P(m,0)
∴PN=|
m|,MP=|
m
2-2m-4|.
∵0<m<+1
∴MN=MP+PN=m-m
2+2m+4=-m
2+3m+4.
(3)过B作BC⊥MN于C
则BC=4-m,OP=m.
∴S
=S△MON
+S△BMN
=MN·OP+MN·BC=MN(OP+BC)
=2(-m
2+3m+4)
=-2(m-)2+.
∵-2<0
∴当m=时,S有最大值.
【方法突破】
所谓“面积分割法”,就是将不能直接利用三角形面积求解时,讲所求三角形的面积分割成几个可以直接利用公式求解的几何图形,那么如何对图形进行合理分割呢?需要注意的是,分割所求图形的直线,往往是过已知点所做的平行于x轴或者y轴的直线。
【学以致用】
1.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
2.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由
2.解:(1)如图1,过点B作BM⊥x轴于M.
由旋转性质知OB=OA=2.
∵∠AOB=120°,∴∠BOM=60°.
∴OM=OB·cos60°=2×=1,BM=OB·sin60°=2×=.
∴点B的坐标为(1,).
(2)设经过A、O、B三点的抛物线的解析式为y=ax
2+bx+c
∵抛物线过原点,∴c=0.
∴
解得
∴所求抛物线的解析式为y=x
2+x.
(3)存在.
如图2,
连接AB,交抛物线的对称轴于点C,连接OC.
∵OB的长为定值,∴要使△BOC的周长最小,必须BC+OC的长最小.
∵点A与点O关于抛物线的对称轴对称,∴OC=AC.
∴BC+OC=BC+AC=AB.
由“两点之间,线段最短”的原理可知:此时BC+OC最小,点C的位置即为所求.
设直线AB的解析式为y=kx+m,将A(-2,0),B(1,)代入,得
解得
∴直线AB的解析式为y=x+.
抛物线的对称轴为直线x==-1,即x=-1.
将x=-1代入直线AB的解析式,得y=×(-1)+=.
∴点C的坐标为(-1,).
(4)△PAB有最大面积.
如图3,过点P作y轴的平行线交AB于点D.
∵S△PAB
=S△PAD+S△PBD
=(yD-yP)(xB-xA)
=[(x+)-(x
2+x)](1+2)
=-x
2-x+
=-(x+)2+
∴当x=-时,△PAB的面积有最大值,最大值为.
此时yP=×(-)2+×(-)=-.
∴此时P点的坐标为(-,-).
x
在中考压轴题中有一类题目是函数综合题,其中有一问涉及了三角形的面积的最值问题.这类题通常会涉及到一个动点,问这个动点运动到什么位置的时候面积最大.对于这类题我们可以先用代数式表示此三角形的面积,表示三角形的面积的时候可以采用构底造高法来求,下面呢我们通过一道例题还讲解一下。
一、构底造高法
【典例探究】(2016 绥化)如图,抛物线经过点A(1,0)和点B(5,0),与y轴交于点C.
(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.
【思路分析】
(3)过P作PQ∥y轴,交直线BC于点Q,P、Q两点的横坐标相同,则可推导出
【解答】解:(1)∵抛物线经过点A(1,0)和点B(5,0),
∴把A、B两点坐标代入可得解得
∴抛物线解析式为
(2)相交,
理由:过A作AD⊥BC于点D,如图,
∵⊙A与BC相切,∴AD为⊙A的半径,
由(1)可知,且,
在Rt△OBC中,由勾股定理可得
∵∠ADB=∠BOC=90°,∠ABD=∠CBO,
∴△ABD∽△CBO,即解得,
∴⊙A与y轴相交;
(3)设,过P作PQ∥y轴,交直线BC于点Q,如图
设直线BC解析式为,把B点坐标代入可求得,∴直线BC的解析式为
,
当时,S△PBC有最大值,点P的坐标为
(本题节选自2016年绥化中考)
【方法突破】
所谓“构底造高法”就是重新构造三角形的底或高,使之能直接利用三角形的面积公式求解.通常构造三角形的底或高的方法是过三角形的一个顶点作x轴或y轴的垂线,与三角形的一条固定边相交,从而确定“底”或“高”。
如下图
过点C作CD∥y轴,则
【学以致用】
1.如图,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,抛物线的对称轴与抛物线交于P、与直线BC相交于点M,连接PB.
(1)求抛物线的解析式;
(2)在(1)中位于第一象限内的抛物线上是否存在点D,使得△BCD的面积最大 若存在,求出D点坐标及△BCD面积最大值;若不存在,请说明理由.
(3)在(1)中的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等 若存在,求出点Q的坐
标;若不存在,请说明理由.
2.(2011 齐齐哈尔)已知:二次函数y=x2+bx+c,其图象对称轴为直线x=1,且经过点(2,﹣).
(1)求此二次函数的解析式.
(2)设该图象与x轴交于B、C两点(B点在C点的左侧),请在此二次函数x轴下方的图象上确定一点E,使△EBC的面积最大,并求出最大面积.
注:二次函数y=ax2+bx+c(a≠0)的对称轴是直线x=﹣.
【分析】(1)利用待定系数法将直线x=1,且经过点(2,﹣)代入二次函数解析式,求二次函数解析式即可;
(2)利用二次函数与x轴相交即y=0,求出即可,再利用E点在x轴下方,且E为顶点坐标时△EBC面积最大,求出即可.
【解答】解:(1)由已知条件得,
解得b=﹣,c=﹣,
∴此二次函数的解析式为y=x2﹣x﹣;
(2)令x2﹣x﹣=0,
∴x1=﹣1,x2=3,
∴B(﹣1,0),C(3,0),
∴BC=4,
∵E点在x轴下方,且△EBC面积最大,
∴E点是抛物线的顶点,其坐标为(1,﹣3),
∴△EBC的面积=×4×3=6.
总结:此题主要考查了待定系数法求二次函数解析式以及求二次函数顶点坐标进而得出三角形面积等知识,根据题意得出E为顶点坐标时△EBC面积最大是解决问题的关键.
3.(2016 湘西州)如图,长方形OABC的OA边在x轴的正半轴上,OC在y轴的正半轴上,抛物线y=ax2+bx经过点B(1,4)和点E(3,0)两点.
(1)求抛物线的解析式;
(2)若点D在线段OC上,且BD⊥DE,BD=DE,求D点的坐标;
(3)在条件(2)下,在抛物线的对称轴上找一点M,使得△BDM的周长为最小,并求△BDM周长的最小值及此时点M的坐标;
(4)在条件(2)下,从B点到E点这段抛物线的图象上,是否存在一个点P,使得△PAD的面积最大?若存在,请求出△PAD面积的最大值及此时P点的坐标;若不存在,请说明理由.
【答案】解:(1)将点B(1,4),E(3,0)的坐标代入抛物线的解析式得:
解得
抛物线的解析式
(2)∵BD⊥DE,∴∠BDE=90°.∴∠BDC+∠EDO=90°.
又∵∠ODE+∠DEO=90°,∴∠BDC=∠DEO.
在△BDC和△DOE中,∴△BDC≌△DEO.
∴OD=AO=1.∴D(0,1).
(3)如图所示,作点B关于抛物线的对称轴的对称点B′,连接B′D交抛物线的对称轴与点M.
,∴点B′的坐标为(2,4).
∵点B与点B′关于对称,∴MB=B′M.∴DM+MB=DM+MB′.
∴当点D、M、B′在一条直线上时,MD+MB有最小值(即△BMD的周长有最小值).
∵由两点间的距离公式可知:,
∴△BDM的最小值为,
设直线B′D的解析式为y=mx+n.
将点D、B′的坐标代入得:解得
∴直线DB′的解析式为
(4)存在.
理由:
如图所示:设点过点P作PG⊥x轴,交直线DA于点G,
∵B(1,4),∴A(1,0),又D(0,1),∴直线AD为,
∴,最大值是
二、平行相切法
【典例探究】
(2015秋 自贡校级月考)如图,抛物线经过A(﹣1,0),B(5,0),C(0,﹣)三点,点P是直线BC下方的抛物线上一动点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使MA+MC的值最小,求点M的坐标;
(3)当点P运动到什么位置时,△PBC的面积最大,并求出此时P点的坐标和△PBC的最大面积.
【考点】二次函数综合题.21世纪教育网
【分析】(1)A(﹣1,0),B(5,0),C(0,﹣)代入y=ax2+bx+c,即可得出抛物线的解析式,
(2)点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,则点M就是BC与抛物线对称轴的交点,把B(5,0),C(0,﹣)代入y=kx+b,求出直线BC的解析式,把抛物线对称轴x=2代入即可得到点M的坐标,
(3)过点P作l∥BC,交y轴于Q点,当l与抛物线只有唯一的公共点P时,△PBC的面积最大,联立方程利用△可求出设此时l的解析式,可求出点P的作坐标,作CN⊥l,利用=求出CN,即可得出△PBC的面积.
【解答】解:(1)设抛物线的解析式为y=ax2+bx+c,把A(﹣1,0),B(5,0),C(0,﹣)代入解析式,
得,解得,
所以抛物线的解析式为y=x2﹣2x﹣.
(2)如图1,点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,
则点M就是BC与抛物线对称轴的交点,
∵抛物线的解析式为y=x2﹣2x﹣.
∴抛物线对称轴x=2,
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,﹣)代入得,解得.
∴直线BC的解析式为y=x﹣,
∵M的横坐标为2,
∴点M的坐标为(2,﹣),
(3)过点P作l∥BC,交y轴于Q点,如图2,
∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=x+n,
∴方程有唯一一组解,即x2﹣2x﹣=x+n有相等的实数解,
整理得x2﹣5x﹣5﹣2n=0,△=52﹣4(﹣5﹣2n)=0,解得n=﹣,y=x﹣,
∴此时P点坐标为(,﹣),
∵Q点坐标为(0,﹣),
作CN⊥l,CQ=OQ﹣OC=﹣=,
∵===,
∴CN= =,
∴△PBC的面积=BC CN=××=.
【方法突破】
所谓“平行相切法”就是作三角形一条固定边的平行线且这条平行线与抛物线“相切”,即与抛物线只有一个交点。这样,就会使得以三角形固定边为底的三角形的高达到最大化,从而三角形的面积也就最大。
【学以致用】
1.如图,已知抛物线与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式:________.
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大 最大面积是多少
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积,若存在,求出P点的坐标;若不存在,请说明理由.
2.(2014秋 古蔺县校级期中)如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.
(1)求抛物线的解析式及点C的坐标;
(2)当点P运动到什么位置时,△PAB的面积最大?最大面积是多少?
(3)当(2)中点P运动到△PAB的面积最大时,x轴上是否存在点D,使△PDB的周长最小?若存在,求出点D的坐标;若不存在.请说明理由.
21世纪教育网
【分析】(1)把A(﹣4,0),B(0,4)代入抛物线y=﹣x2+bx+c,可得出抛物线解析式,当y=0时即可得出点C的坐标.
(2)设y=x+b与抛物线y=﹣x2﹣3x+4只有一个交点时,△PAB的面积最大,利用判别式求出b的值,再联立可得出点P的坐标,过点B作BM⊥PN交PN于点M,利用三角函数求出BM,再利用△PAB的面积公式即可求出答案.
(3)连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.先求出点B′的坐标,再利用坐标求出PB′所在的直线,即可求出与x轴的交点D的坐标.
【解答】解:(1)∵直线y=x+4与x轴、y轴分别交于A、B两点,
∴A(﹣4,0),B(0,4)抛物线y=﹣x2+bx+c经过A、B两点,可得,解得,
∴抛物线解析式为y=﹣x2﹣3x+4.
令y=0,得﹣x2﹣3x+4=0,
解得x1=﹣4,x2=1,
∴C(1,0).
(2)如图1,
设y=x+b与抛物线y=﹣x2﹣3x+4只有一个交点时,△PAB的面积最大,
∵由x+b=﹣x2﹣3x+4化简x2+4x+b﹣4只有一个解,得△=16﹣4×(b﹣4)=32﹣4b=0,解得b=8.
∴y=x+8,
∴联立得方程组得,
解得,
∴P(﹣2,6)
过点B作BM⊥PN交PN于点M,
∵BN=ON﹣OB=8﹣4=4,sin∠MNB=,
∴BM=4×=2,
△PAB的面积=AB BM=×4×2=8.
(3)存在.如图2,
连接BP,作点B关于原点O的对称点B′,连接B′P,交x轴于点D,这时△PDB的周长最小.
∵点B(0,4),
∴点B′(0,﹣4),
∵P(﹣2,6)
∴设PB′所在的直线为y=kx+b得,
解得
∴PB′所在的直线为y=﹣5x﹣4,
点D的坐标为(﹣,0).
【点评】本题主要考查了二次函数图象与其他函数图象相结合问题,解题的关键是根据一次函数系数与图象的位置关系判断出图象特征.
三、面积分割法
【典例探究】
如图,已知抛物线与直线y=x交于点A、B两点,A、B的横坐标分别为-1和4.
(1)求此抛物线的解析式.
(2)若平行于y轴的直线x=m()与抛物线交于点M,与直线y=x交于点N,交x轴于点P,求线段MN的长(用含m的代数式表示).
(3)在(2)的条件下,连接OM、BM,是否存在m的值,使得△BOM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
分析:(1)由于A、B两点是抛物线与直线的交点,说明这两点既在直线上又在抛物线上,将两点横坐标代入直线解析式,得到这两点的坐标,再将亮点坐标代入抛物线解析式可得。(2)先根据条件确定N点坐标,用含有m的代数式表示出MP和NP的长度,则不难表示出MN的长度。(3)由于m值不固定,导致△BOM的形状也是动态的,不能直接利用三角形面积公式表示出来,因此我们将△BOM的面积分割成△MON和△BNM两个三角形面积之和。
解:(1)由题意知A(-1,-1),B(4,4),代入y=ax
2+bx-4,得
,
.
∴所求抛物线的解析式为y=x
2-2x-4
(2)由x=m和y=x,得交点N(m,m)
同理可得M(m,m
2-2m-4),P(m,0)
∴PN=|
m|,MP=|
m
2-2m-4|.
∵0<m<+1
∴MN=MP+PN=m-m
2+2m+4=-m
2+3m+4.
(3)过B作BC⊥MN于C
则BC=4-m,OP=m.
∴S
=S△MON
+S△BMN
=MN·OP+MN·BC=MN(OP+BC)
=2(-m
2+3m+4)
=-2(m-)2+.
∵-2<0
∴当m=时,S有最大值.
【方法突破】
所谓“面积分割法”,就是将不能直接利用三角形面积求解时,讲所求三角形的面积分割成几个可以直接利用公式求解的几何图形,那么如何对图形进行合理分割呢?需要注意的是,分割所求图形的直线,往往是过已知点所做的平行于x轴或者y轴的直线。
【学以致用】
1.如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
2.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由
2.解:(1)如图1,过点B作BM⊥x轴于M.
由旋转性质知OB=OA=2.
∵∠AOB=120°,∴∠BOM=60°.
∴OM=OB·cos60°=2×=1,BM=OB·sin60°=2×=.
∴点B的坐标为(1,).
(2)设经过A、O、B三点的抛物线的解析式为y=ax
2+bx+c
∵抛物线过原点,∴c=0.
∴
解得
∴所求抛物线的解析式为y=x
2+x.
(3)存在.
如图2,
连接AB,交抛物线的对称轴于点C,连接OC.
∵OB的长为定值,∴要使△BOC的周长最小,必须BC+OC的长最小.
∵点A与点O关于抛物线的对称轴对称,∴OC=AC.
∴BC+OC=BC+AC=AB.
由“两点之间,线段最短”的原理可知:此时BC+OC最小,点C的位置即为所求.
设直线AB的解析式为y=kx+m,将A(-2,0),B(1,)代入,得
解得
∴直线AB的解析式为y=x+.
抛物线的对称轴为直线x==-1,即x=-1.
将x=-1代入直线AB的解析式,得y=×(-1)+=.
∴点C的坐标为(-1,).
(4)△PAB有最大面积.
如图3,过点P作y轴的平行线交AB于点D.
∵S△PAB
=S△PAD+S△PBD
=(yD-yP)(xB-xA)
=[(x+)-(x
2+x)](1+2)
=-x
2-x+
=-(x+)2+
∴当x=-时,△PAB的面积有最大值,最大值为.
此时yP=×(-)2+×(-)=-.
∴此时P点的坐标为(-,-).
x
同课章节目录
