矩形的性质课件
图片预览










文档简介
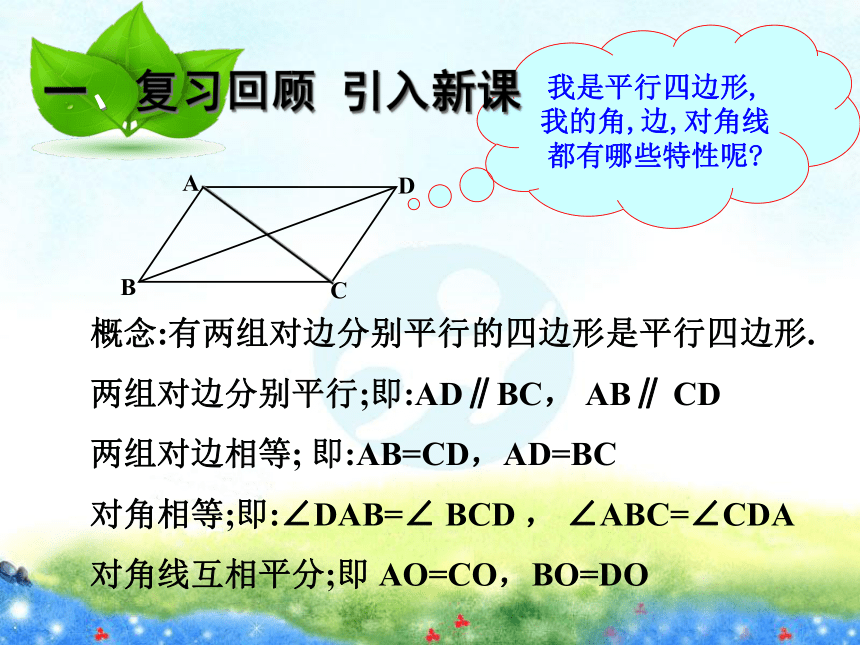
课件33张PPT。古来一切有成就的人,都很严肃地对待自己的生命,当他活着一天,总要尽量多劳动,多工作,多学习,不肯虚度年华,不让时间白白地浪费掉。 —— 邓拓我是平行四边形,我的角,边,对角线都有哪些特性呢?概念:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行;即:AD∥BC, AB∥ CD
两组对边相等; 即:AB=CD,AD=BC
对角相等;即:∠DAB=∠ BCD , ∠ABC=∠CDA
对角线互相平分;即 AO=CO,BO=DO观察并思考下面这些物体的形状是平行四边形吗?它们的特殊之处在什么地方?餐桌瓷砖木门纸张电脑显示器有一个角是直角的特殊平行四边形。 用四段木条做一个 ABCD的活动 木框,将其直立在桌面上轻轻地推动点D,你会发现什么?试一试?OO┓90°平行四边形矩形 南阳市鸭河工区鸭河中学 19.1 矩形的性质学习目标:1.熟练掌握矩形的定义和性质,理解矩形性质的探究过程.
2.掌握矩形与平行四边形的区别与联系.
3.能利用矩形的性质进行简单的计算和证明.
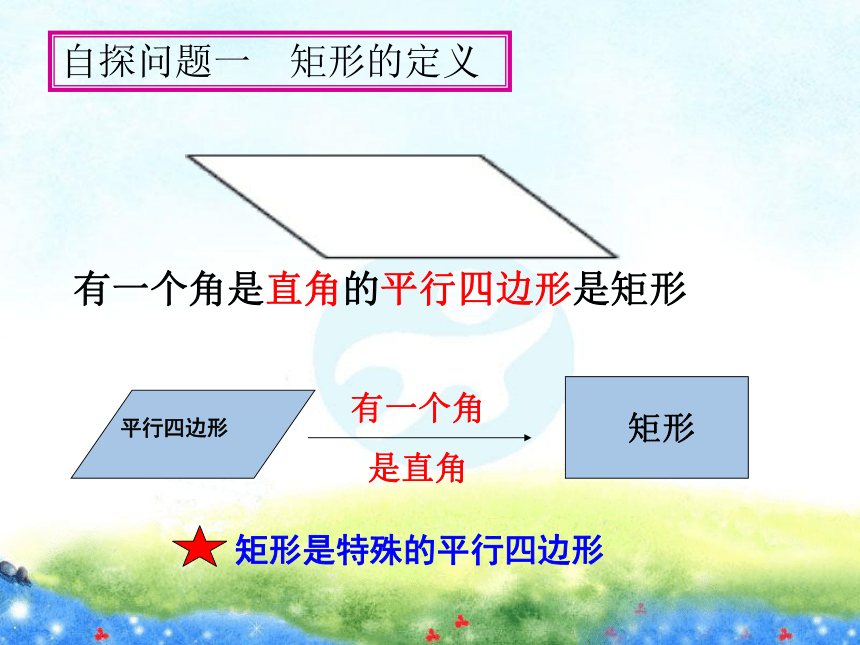
二、设疑自探二、设疑自探≤请同学们自学课本98页—99页,完成自探提示中的“问题1”和“问题2”.1. 解疑自探有一个角是直角的平行四边形是矩形自探问题一 矩形的定义 门课本五星红旗生活中矩形的例子
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD自探问题二 矩形的特殊性质 求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形 ∠A=90°又 ∵ 矩形ABCD中∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角矩形的两条对角线相等.从角上看:从对角线上看:观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴? 矩形的对称性 比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形O2. 解疑合探例题点拨 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?解∵△AOB、△BOC、△COD和△AOD四个 小三角形周长的和为86cm,
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
= AB+BC+CD+DA+2(AC+BD)
=86
又∵AC=BD=13(矩形的对角线相等)
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
一、选择题
1、矩形具有而一般平行四边形不具有
的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C牛刀小试 课堂检测 2.下列说法错误的是( ).
(A)矩形的对角线互相平分
(B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形
(D)有一个角是直角的平行四边形叫做矩形C1.有一个角是直角的_____________叫做
矩形.作为特殊的平行四边形,矩形既是中
心对称图形,也是轴对称图形,对称轴为通
过对边_______的直线.
2.矩形的四个角都是________;矩形的对
角线_______.平行四边形中点直角相等二、试一试:四边形ABCD是矩形
3.若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
4.若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
5104828OABCD公平,因为OA=OC=OB=OD四.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 通过本节课的学习,你有什么困惑?三、质疑再探 1.根据本节学习内容,请同学们自编习题,同桌
交流解答。四、运用拓展 2.矩形ABCD的周长为56cm,对角线AC、BD交于O,
△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少?拓展提高你来总结课堂小结本题课你有什么收获或感想?
请学科班长评价一下本节课的活动情况!教材100页练习题1、2、3.
再 见祝同学们:
天天快乐,
学业有成。
两组对边分别平行;即:AD∥BC, AB∥ CD
两组对边相等; 即:AB=CD,AD=BC
对角相等;即:∠DAB=∠ BCD , ∠ABC=∠CDA
对角线互相平分;即 AO=CO,BO=DO观察并思考下面这些物体的形状是平行四边形吗?它们的特殊之处在什么地方?餐桌瓷砖木门纸张电脑显示器有一个角是直角的特殊平行四边形。 用四段木条做一个 ABCD的活动 木框,将其直立在桌面上轻轻地推动点D,你会发现什么?试一试?OO┓90°平行四边形矩形 南阳市鸭河工区鸭河中学 19.1 矩形的性质学习目标:1.熟练掌握矩形的定义和性质,理解矩形性质的探究过程.
2.掌握矩形与平行四边形的区别与联系.
3.能利用矩形的性质进行简单的计算和证明.
二、设疑自探二、设疑自探≤请同学们自学课本98页—99页,完成自探提示中的“问题1”和“问题2”.1. 解疑自探有一个角是直角的平行四边形是矩形自探问题一 矩形的定义 门课本五星红旗生活中矩形的例子
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.猜想2:矩形的对角线相等.ABCD自探问题二 矩形的特殊性质 求证:矩形的四个角都是直角.已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A=∠B=∠C=∠D=90°证明: ∵四边形ABCD是矩形 ∠A=90°又 ∵ 矩形ABCD中∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角已知:如图,四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 即矩形的对角线相等求证:矩形的对角线相等矩形特殊的性质矩形的四个角都是直角矩形的两条对角线相等.从角上看:从对角线上看:观察并思考下面这些物体是什么形状,它们是轴对称图形吗?是中心对称图形吗?有几条对称轴? 矩形的对称性 比一比,知关系对边平行
且相等对角相等
邻角互补对角线互
相平分中心对称图形对边平行
且相等四个角
为直角对角线互相
平分且相等中心对称图形
轴对称图形O2. 解疑合探例题点拨 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?解∵△AOB、△BOC、△COD和△AOD四个 小三角形周长的和为86cm,
∴AB+BC+CD+DA+2(OA+OB+OC+OD)
= AB+BC+CD+DA+2(AC+BD)
=86
又∵AC=BD=13(矩形的对角线相等)
∴AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
一、选择题
1、矩形具有而一般平行四边形不具有
的性质是 ( )
A.对角相等
B.对边相等
C.对角线相等
D.对角线互相平分
C牛刀小试 课堂检测 2.下列说法错误的是( ).
(A)矩形的对角线互相平分
(B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形
(D)有一个角是直角的平行四边形叫做矩形C1.有一个角是直角的_____________叫做
矩形.作为特殊的平行四边形,矩形既是中
心对称图形,也是轴对称图形,对称轴为通
过对边_______的直线.
2.矩形的四个角都是________;矩形的对
角线_______.平行四边形中点直角相等二、试一试:四边形ABCD是矩形
3.若已知AB=8㎝,AD=6㎝,
则AC= ㎝ OB= ㎝
4.若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝
矩形的面积= ㎝2
5104828OABCD公平,因为OA=OC=OB=OD四.如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长?∴AC与BD相等且互相平分∴ OA=OB∵ ∠AOB=60°∴ △AOB是等边三角形∴ OA=AB=4(㎝)∴ 矩形的对角线长 AC=BD=2OA=8(㎝)解:∵ 四边形ABCD是矩形 通过本节课的学习,你有什么困惑?三、质疑再探 1.根据本节学习内容,请同学们自编习题,同桌
交流解答。四、运用拓展 2.矩形ABCD的周长为56cm,对角线AC、BD交于O,
△BOC和△AOB的周长差是4cm,那么矩形各边的
长是多少?拓展提高你来总结课堂小结本题课你有什么收获或感想?
请学科班长评价一下本节课的活动情况!教材100页练习题1、2、3.
再 见祝同学们:
天天快乐,
学业有成。
