19.2.2菱形的判定课件
图片预览







文档简介
课件29张PPT。一起放飞理想的翅膀
在知识的天空中自由翱翔
19.2.2菱形的判定 复习与回顾:想一想:
1.菱形的定义?
2.菱形比平行四边形多了哪些性质?
?
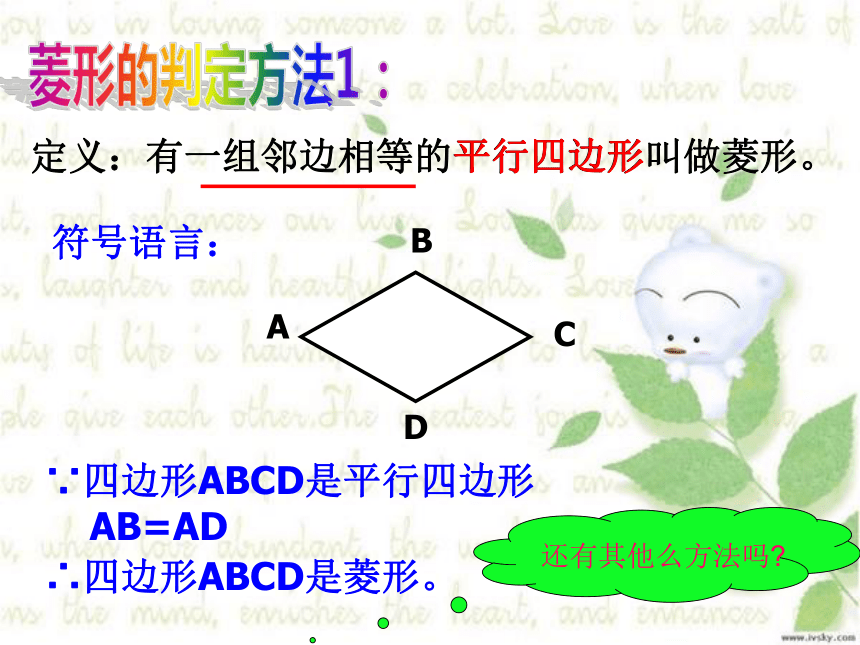
?菱形有一组邻边相等的平行四边形叫做菱形.具有平行四边形的一切性质性质边角对角线互相垂直且平分每一组对角判定四条边都相等想一想: 在学习平行四边形的判定和矩形的判定时,我们首先想到的一种方法是什么?那么类比它们,判定菱形的基本方法是什么?ACBD定义:有一组邻边相等的平行四边形叫做菱形。平行四边形符号语言:∵四边形ABCD是平行四边形
AB=AD∴四边形ABCD是菱形。菱形的判定方法1:学习目标:
1.掌握菱形的判定定理及证明方法。
2.经历菱形判定证明,学会解证明题思路和方法。
3.能运用菱形的判定定理进行计算与证明。菱形的判定1、菱形的判定定理1、2的内容分别是什么?
2、利用菱形的定义去证明这两个命题?
3、菱形的判定定理怎样用数学语言去叙述?
自学5分钟,不能独立解决的问题上作
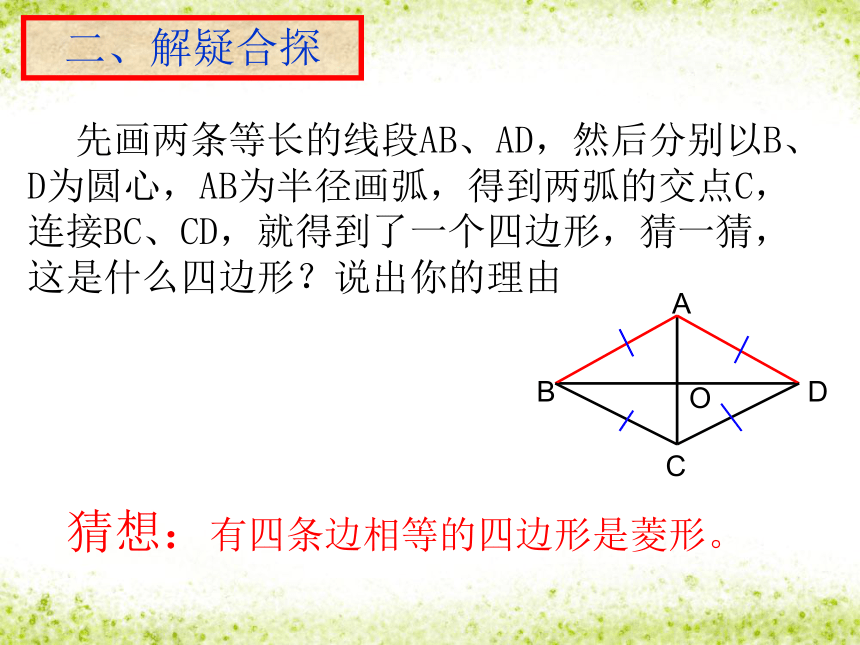
标记,便于同学交流或组内讨论。自探提示:一、设疑自探 先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由猜想:有四条边相等的四边形是菱形。O二、解疑合探命题:有四条边相等的四边形是菱形。已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵在四边形ABCD中AB=BC=CD=DA∴四边形ABCD是菱形菱形的判定定理1:数学语言探究二 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?猜想:对角线互相垂直的平行四边形是菱形.命题:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC 判定定理2:对角线互相垂直的平行四边形是菱形∵在□ABCD中,AC⊥BD∴ □ABCD是菱形数学语言菱形常用的判定方法:有一组邻边相等的平行四边形叫做菱形有四条边相等的四边形是菱形。归纳:对角线互相垂直的平行四边形是菱形。三、质疑再探:有三条边相等的四边形是菱形吗?通过以上学习你对本节内容还有哪些疑惑或新的发现?1、老师说下列三个图形都是菱形,你相信吗? 有一组邻边相等的平行四边形叫做菱形 对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形。尝试练习:2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( ) ╳√ ╳ ╳ 3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。矩菱矩菱(1).下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C(2).对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C(3).下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BDC4、选择:想一想 S h u x u e 小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:目标2:思想方法 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵∠3=∠4
∴△AEO≌△CFO∵AE=EC
∴四边形AFCE是菱形∴四边形AFCE是平行四边形证明:
∵EF是AC的垂直平分线
∴OA=OC,AE=EC1234目标2:思想方法∴OE=OF 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:1234证明:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵OA=OC,∠3=∠4
∴△AEO≌△CFO∴AE=CF∵EF是AC的垂直平分线
∴AE=EC,AF=FC∴AE=EC=CF=AF
∴四边形AFCE是菱形目标2:思想方法 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:1234证明:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵OA=OC,∠3=∠4
∴△AEO≌△CFO∴OE=OF∵EF是AC的垂直平分线
∴OA=OC, AC⊥EF
目标2:思想方法∴四边形AFCE是平行四边形∴四边形AFCE是菱形1、进一步熟练了菱形的判定方法;2、能灵活得看待每一个题目,学会一题多证,一题多解;3、利用所学知识,会解决生活中的实际问题。这节课你有何收获?
2.设计一个由一条对角线在同一条直线上的四个菱形
交叉组成的花边图案,其长为15厘米,宽为4厘米,
试画出它的图形。
布置作业:1.习题19.2 第3、5题请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB思考:目标3:知识应用再见欢迎指导
在知识的天空中自由翱翔
19.2.2菱形的判定 复习与回顾:想一想:
1.菱形的定义?
2.菱形比平行四边形多了哪些性质?
?
?菱形有一组邻边相等的平行四边形叫做菱形.具有平行四边形的一切性质性质边角对角线互相垂直且平分每一组对角判定四条边都相等想一想: 在学习平行四边形的判定和矩形的判定时,我们首先想到的一种方法是什么?那么类比它们,判定菱形的基本方法是什么?ACBD定义:有一组邻边相等的平行四边形叫做菱形。平行四边形符号语言:∵四边形ABCD是平行四边形
AB=AD∴四边形ABCD是菱形。菱形的判定方法1:学习目标:
1.掌握菱形的判定定理及证明方法。
2.经历菱形判定证明,学会解证明题思路和方法。
3.能运用菱形的判定定理进行计算与证明。菱形的判定1、菱形的判定定理1、2的内容分别是什么?
2、利用菱形的定义去证明这两个命题?
3、菱形的判定定理怎样用数学语言去叙述?
自学5分钟,不能独立解决的问题上作
标记,便于同学交流或组内讨论。自探提示:一、设疑自探 先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?说出你的理由猜想:有四条边相等的四边形是菱形。O二、解疑合探命题:有四条边相等的四边形是菱形。已知:在四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵在四边形ABCD中AB=BC=CD=DA∴四边形ABCD是菱形菱形的判定定理1:数学语言探究二 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形?猜想:对角线互相垂直的平行四边形是菱形.命题:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC 判定定理2:对角线互相垂直的平行四边形是菱形∵在□ABCD中,AC⊥BD∴ □ABCD是菱形数学语言菱形常用的判定方法:有一组邻边相等的平行四边形叫做菱形有四条边相等的四边形是菱形。归纳:对角线互相垂直的平行四边形是菱形。三、质疑再探:有三条边相等的四边形是菱形吗?通过以上学习你对本节内容还有哪些疑惑或新的发现?1、老师说下列三个图形都是菱形,你相信吗? 有一组邻边相等的平行四边形叫做菱形 对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形。尝试练习:2、判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形; ( )
(2)对角线互相垂直平分的四边形是菱形;( )
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形; ( )
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形. ( ) ╳√ ╳ ╳ 3、□ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。矩菱矩菱(1).下列命题中正确的是( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C(2).对角线互相垂直且平分的四边形是( )
A.矩形 B.一般的平行四边形
C.菱形 D.以上都不对C(3).下列条件中,不能判定四边形ABCD为菱形的是( )
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BDC4、选择:想一想 S h u x u e 小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗? 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:目标2:思想方法 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵∠3=∠4
∴△AEO≌△CFO∵AE=EC
∴四边形AFCE是菱形∴四边形AFCE是平行四边形证明:
∵EF是AC的垂直平分线
∴OA=OC,AE=EC1234目标2:思想方法∴OE=OF 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:1234证明:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵OA=OC,∠3=∠4
∴△AEO≌△CFO∴AE=CF∵EF是AC的垂直平分线
∴AE=EC,AF=FC∴AE=EC=CF=AF
∴四边形AFCE是菱形目标2:思想方法 已知:□ABCD的对角线AC的垂直平分线与边AD 、BC分别交于E、F。 求证:四边形AFCE是菱形。例题解析:1234证明:
∵四边形ABCD是平行四边形
∴AD∥BC
∴∠1=∠2
∵OA=OC,∠3=∠4
∴△AEO≌△CFO∴OE=OF∵EF是AC的垂直平分线
∴OA=OC, AC⊥EF
目标2:思想方法∴四边形AFCE是平行四边形∴四边形AFCE是菱形1、进一步熟练了菱形的判定方法;2、能灵活得看待每一个题目,学会一题多证,一题多解;3、利用所学知识,会解决生活中的实际问题。这节课你有何收获?
2.设计一个由一条对角线在同一条直线上的四个菱形
交叉组成的花边图案,其长为15厘米,宽为4厘米,
试画出它的图形。
布置作业:1.习题19.2 第3、5题请你动脑筋把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?ACDB思考:目标3:知识应用再见欢迎指导
