2016-2017学年高一数学人教B版必修1学案(课堂探究 ):2.1.2函数的表示方法
文档属性
| 名称 | 2016-2017学年高一数学人教B版必修1学案(课堂探究 ):2.1.2函数的表示方法 |

|
|
| 格式 | zip | ||
| 文件大小 | 705.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-17 00:00:00 | ||
图片预览

文档简介
课堂探究
探究一
画函数图象
图象的画法常见的有两种:描点法、变换作图法.
1.描点法的一般步骤是:列表、描点、连线;
列表——先找出一些(有代表性的)自变量x,并计算出与这些自变量相对应的函数值f(x),用表格的形式表示出来;
描点——从表中得到一系列的点(x,f(x)),在坐标平面上描出这些点;
连线——用光滑曲线把这些点按自变量由小到大的顺序连接起来.
2.变换作图法常用的有水平平移变换、竖直平移变换、翻折变换等.
3.作函数图象时应特别注意:顶点、端点、图象与x轴的交点等这些特殊点.
4.作图时应首先看清函数的定义域.
【典型例题1】
作出下列函数的图象:
(1)y=-x+1,x∈Z;
(2)y=2x2-4x-3(0≤x<3);
(3)y=|1-x|;
(4)y=
思路分析:作函数图象,首先明确函数的定义域,其次明确函数图象的形状,体会定义域对图象的控制作用,处理好端点.如,第(4)小题x=0时的情况.作图时,如第(2)小题,先不受定义域限制作出完整的抛物线,然后再根据定义域截取.函数图象的形状可以是一条或几条无限长的平滑曲线,也可以是一些点、一些线段、一段曲线等.
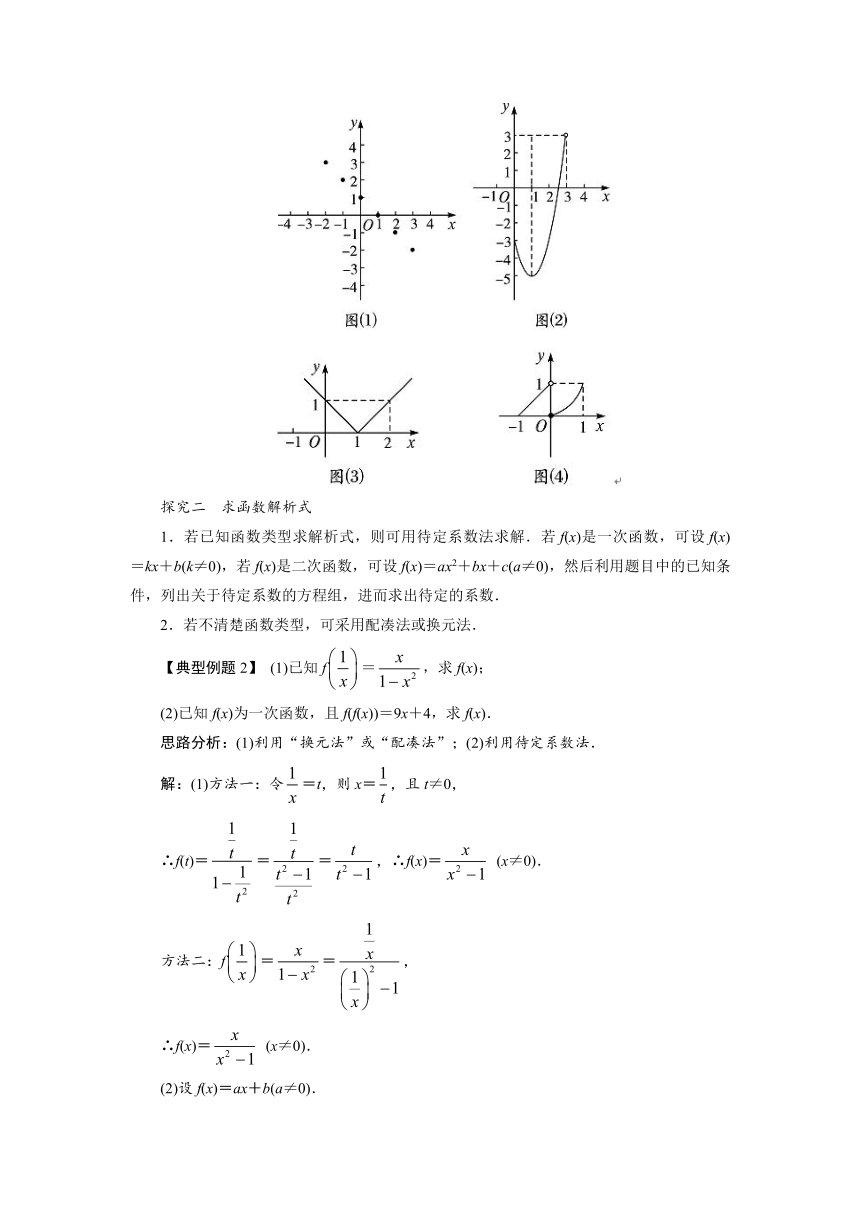
解:(1)定义域为Z,所以图象为离散的点.图象如图(1)所示.
(2)y=2x2-4x-3=2(x-1)2-5(0≤x<3),定义域不是R,因此图象不是完整的抛物线,而是抛物线的一部分.图象如图(2)所示.
(3)先根据绝对值的定义去掉绝对值号,再写成分断函数y=图象如图(3)所示.
(4)这个函数的图象由两部分组成.当0≤x≤1时,为抛物线y=x2的一段;当-1≤x<0时,为直线y=x+1的一段.图象如图(4)所示.
探究二
求函数解析式
1.若已知函数类型求解析式,则可用待定系数法求解.若f(x)是一次函数,可设f(x)=kx+b(k≠0),若f(x)是二次函数,可设f(x)=ax2+bx+c(a≠0),然后利用题目中的已知条件,列出关于待定系数的方程组,进而求出待定的系数.
2.若不清楚函数类型,可采用配凑法或换元法.
【典型例题2】
(1)已知f=,求f(x);
(2)已知f(x)为一次函数,且f(f(x))=9x+4,求f(x).
思路分析:(1)利用“换元法”或“配凑法”;(2)利用待定系数法.
解:(1)方法一:令=t,则x=,且t≠0,
∴f(t)===,∴f(x)=
(x≠0).
方法二:f==,
∴f(x)=
(x≠0).
(2)设f(x)=ax+b(a≠0).
f(f(x))=af(x)+b=a(ax+b)+b=a2x+ab+b.
由题设知解得或
∴f(x)=3x+1或f(x)=-3x-2.
探究三
分段函数及其应用
求解分段函数问题三注意
1.求f(f(a))的值时,应从内到外依次取值,直到求出值为止.
2.已知函数值,求自变量的值时,切记要进行检验.解题时一定要注意自变量的范围,只有在自变量确定的范围内才可以进行运算.
3.已知f(x),解关于f(x)的不等式时,要先在每一段内求交集,最后求并集.
【典型例题3】
已知f(x)=若f(x)>2,求x的取值范围.
思路分析:在x≥-2时,由x+2>2,解得x>0后,需与x≥-2求交集,得x>0;当x<-2时,由-x-2>2,得x<-4,与x<-2求交集,得x<-4.然后求x>0与x<-4的并集得最后结果.
解:当x≥-2时,f(x)=x+2,由f(x)>2,得x+2>2,解得x>0,故x>0;
当x<-2时,f(x)=-x-2,由f(x)>2,得-x-2>2,解得x<-4,故x<-4.
综上可得,x>0或x<-4.
【典型例题4】
已知函数f(x)=
(1)求f(-8),f,f,f的值;
(2)作出函数的简图;
(3)求函数的值域.
思路分析:给出的函数是分段函数,应注意在不同的自变量取值范围内有不同的解析式.
(1)根据自变量的值,选用相应关系式求函数值.
(2)在不同的区间,依次画出函数图象.
解:函数的定义域为[-1,0)∪[0,1)∪[1,2]=[-1,2].
(1)因为-8 [-1,2],所以f(-8)无意义.
当x∈[-1,0)时,f(x)=-x,
所以f=-=.
当x∈[0,1)时,f(x)=x2,所以f=2=.
当x∈[1,2]时,f(x)=x,所以f=.
(2)根据题中函数的表达式,在平面直角坐标系中作出的函数图象如图所示.
(3)由(2)中画出的图象可知,函数的值域为[0,2].
探究四
易错辨析
易错点 缺乏检验意识而致误
【典型例题5】
已知f(x)=若f(a)=,求a的值.
错解:∵f(a)=
∴令|a-1|-2=,得a=或a=-.
再令=,得a=±2.
综上可知满足f(a)=的a的值为-,,±2.
错因分析:没有对求得的a的值进行验证.
正解:∵f(a)=
∴当|a|≤1时,令|a-1|-2=,
解得a=或a=-.
又∵|a|≤1,
∴a=和a=-均不符合题意,舍去;
当|a|>1时,令=,
解得a=±2,均符合|a|>1.综上,符合题意的a的值为±2.
点评对于分段函数,无论是求函数值,还是求自变量,都要看清楚每一段解析式所对应的自变量的取值范围,不能张冠李戴,也不能忘记检验.
探究一
画函数图象
图象的画法常见的有两种:描点法、变换作图法.
1.描点法的一般步骤是:列表、描点、连线;
列表——先找出一些(有代表性的)自变量x,并计算出与这些自变量相对应的函数值f(x),用表格的形式表示出来;
描点——从表中得到一系列的点(x,f(x)),在坐标平面上描出这些点;
连线——用光滑曲线把这些点按自变量由小到大的顺序连接起来.
2.变换作图法常用的有水平平移变换、竖直平移变换、翻折变换等.
3.作函数图象时应特别注意:顶点、端点、图象与x轴的交点等这些特殊点.
4.作图时应首先看清函数的定义域.
【典型例题1】
作出下列函数的图象:
(1)y=-x+1,x∈Z;
(2)y=2x2-4x-3(0≤x<3);
(3)y=|1-x|;
(4)y=
思路分析:作函数图象,首先明确函数的定义域,其次明确函数图象的形状,体会定义域对图象的控制作用,处理好端点.如,第(4)小题x=0时的情况.作图时,如第(2)小题,先不受定义域限制作出完整的抛物线,然后再根据定义域截取.函数图象的形状可以是一条或几条无限长的平滑曲线,也可以是一些点、一些线段、一段曲线等.
解:(1)定义域为Z,所以图象为离散的点.图象如图(1)所示.
(2)y=2x2-4x-3=2(x-1)2-5(0≤x<3),定义域不是R,因此图象不是完整的抛物线,而是抛物线的一部分.图象如图(2)所示.
(3)先根据绝对值的定义去掉绝对值号,再写成分断函数y=图象如图(3)所示.
(4)这个函数的图象由两部分组成.当0≤x≤1时,为抛物线y=x2的一段;当-1≤x<0时,为直线y=x+1的一段.图象如图(4)所示.
探究二
求函数解析式
1.若已知函数类型求解析式,则可用待定系数法求解.若f(x)是一次函数,可设f(x)=kx+b(k≠0),若f(x)是二次函数,可设f(x)=ax2+bx+c(a≠0),然后利用题目中的已知条件,列出关于待定系数的方程组,进而求出待定的系数.
2.若不清楚函数类型,可采用配凑法或换元法.
【典型例题2】
(1)已知f=,求f(x);
(2)已知f(x)为一次函数,且f(f(x))=9x+4,求f(x).
思路分析:(1)利用“换元法”或“配凑法”;(2)利用待定系数法.
解:(1)方法一:令=t,则x=,且t≠0,
∴f(t)===,∴f(x)=
(x≠0).
方法二:f==,
∴f(x)=
(x≠0).
(2)设f(x)=ax+b(a≠0).
f(f(x))=af(x)+b=a(ax+b)+b=a2x+ab+b.
由题设知解得或
∴f(x)=3x+1或f(x)=-3x-2.
探究三
分段函数及其应用
求解分段函数问题三注意
1.求f(f(a))的值时,应从内到外依次取值,直到求出值为止.
2.已知函数值,求自变量的值时,切记要进行检验.解题时一定要注意自变量的范围,只有在自变量确定的范围内才可以进行运算.
3.已知f(x),解关于f(x)的不等式时,要先在每一段内求交集,最后求并集.
【典型例题3】
已知f(x)=若f(x)>2,求x的取值范围.
思路分析:在x≥-2时,由x+2>2,解得x>0后,需与x≥-2求交集,得x>0;当x<-2时,由-x-2>2,得x<-4,与x<-2求交集,得x<-4.然后求x>0与x<-4的并集得最后结果.
解:当x≥-2时,f(x)=x+2,由f(x)>2,得x+2>2,解得x>0,故x>0;
当x<-2时,f(x)=-x-2,由f(x)>2,得-x-2>2,解得x<-4,故x<-4.
综上可得,x>0或x<-4.
【典型例题4】
已知函数f(x)=
(1)求f(-8),f,f,f的值;
(2)作出函数的简图;
(3)求函数的值域.
思路分析:给出的函数是分段函数,应注意在不同的自变量取值范围内有不同的解析式.
(1)根据自变量的值,选用相应关系式求函数值.
(2)在不同的区间,依次画出函数图象.
解:函数的定义域为[-1,0)∪[0,1)∪[1,2]=[-1,2].
(1)因为-8 [-1,2],所以f(-8)无意义.
当x∈[-1,0)时,f(x)=-x,
所以f=-=.
当x∈[0,1)时,f(x)=x2,所以f=2=.
当x∈[1,2]时,f(x)=x,所以f=.
(2)根据题中函数的表达式,在平面直角坐标系中作出的函数图象如图所示.
(3)由(2)中画出的图象可知,函数的值域为[0,2].
探究四
易错辨析
易错点 缺乏检验意识而致误
【典型例题5】
已知f(x)=若f(a)=,求a的值.
错解:∵f(a)=
∴令|a-1|-2=,得a=或a=-.
再令=,得a=±2.
综上可知满足f(a)=的a的值为-,,±2.
错因分析:没有对求得的a的值进行验证.
正解:∵f(a)=
∴当|a|≤1时,令|a-1|-2=,
解得a=或a=-.
又∵|a|≤1,
∴a=和a=-均不符合题意,舍去;
当|a|>1时,令=,
解得a=±2,均符合|a|>1.综上,符合题意的a的值为±2.
点评对于分段函数,无论是求函数值,还是求自变量,都要看清楚每一段解析式所对应的自变量的取值范围,不能张冠李戴,也不能忘记检验.
