2016-2017学年高一数学人教B版必修1学案(课堂探究 ):3.2.2对数函数
文档属性
| 名称 | 2016-2017学年高一数学人教B版必修1学案(课堂探究 ):3.2.2对数函数 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-17 00:00:00 | ||
图片预览

文档简介
课堂探究
探究一
求对数函数的定义域
求对数函数定义域的步骤
【典型例题1】(1)函数f(x)=+ln(4-x)的定义域为( )
A.[-1,4)
B.(-1,+∞)
C.(-1,4)
D.(4,+∞)
(2)函数y=loga
(a>0,a≠1)的定义域为__________.
解析:(1)由题意可知解得x∈[-1,4),故选A.
(2)由题意可得>0,又∵偶次根号下非负,∴x-1>0,即x>1.
∴函数y=loga
(a>0,a≠1)的定义域为(1,+∞).
答案:(1)A (2)(1,+∞)
探究二
对数函数的图象
对数函数图象的变化规律:
1.对于几个底数都大于1的对数函数,底数越大,函数图象向右的方向越接近x轴;对于几个底数都大于0且小于1的对数函数,底数越大,函数图象向右的方向越远离x轴.以上规律可总结成x>1时“底大图低”.实际上,作出直线y=1,它与各图象交点的横坐标即为各函数的底数的大小,如图所示.
2.当a>1时,图象向下无限接近于y轴;当03.牢记特殊点:对数函数y=logax(a>0,且a≠1)的图象经过(1,0),(a,1),.
【典型例题2】
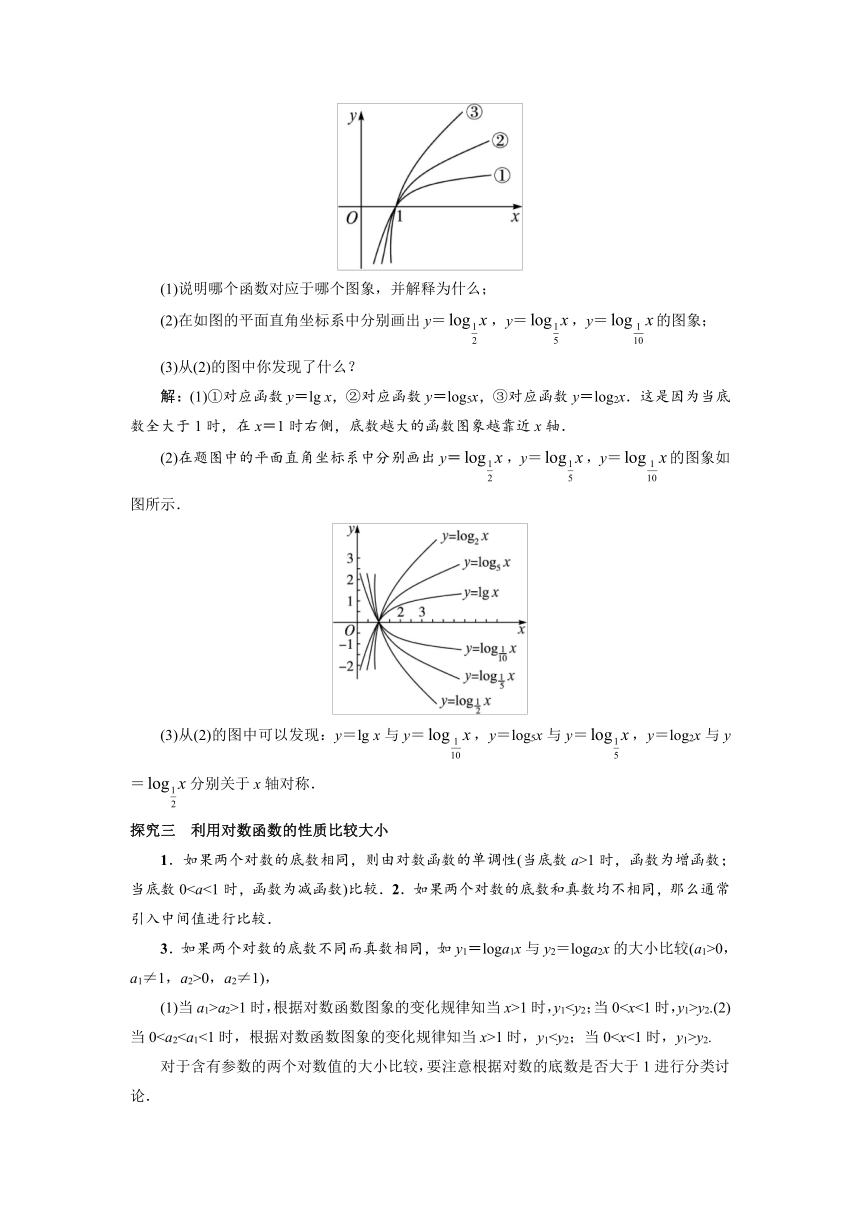
函数y=log2x,y=log5x,y=lg
x的图象如图所示.
(1)说明哪个函数对应于哪个图象,并解释为什么;
(2)在如图的平面直角坐标系中分别画出y=,y=,y=的图象;
(3)从(2)的图中你发现了什么?
解:(1)①对应函数y=lg
x,②对应函数y=log5x,③对应函数y=log2x.这是因为当底数全大于1时,在x=1时右侧,底数越大的函数图象越靠近x轴.
(2)在题图中的平面直角坐标系中分别画出y=,y=,y=的图象如图所示.
(3)从(2)的图中可以发现:y=lg
x与y=,y=log5x与y=,y=log2x与y=分别关于x轴对称.
探究三
利用对数函数的性质比较大小
1.如果两个对数的底数相同,则由对数函数的单调性(当底数a>1时,函数为增函数;当底数03.如果两个对数的底数不同而真数相同,如y1=loga1x与y2=loga2x的大小比较(a1>0,a1≠1,a2>0,a2≠1),
(1)当a1>a2>1时,根据对数函数图象的变化规律知当x>1时,y1y2.(2)当01时,y1y2.
对于含有参数的两个对数值的大小比较,要注意根据对数的底数是否大于1进行分类讨论.
【典型例题3】比较大小:
(1)log0.27与log0.29;
(2)log35与log65;
(3)(lg
m)1.9与(lg
m)2.1(m>1);
(4)log85与lg
4.
解:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两个函数值,由y=log0.2x在(0,+∞)上是减函数,得log0.27>log0.29.
(2)函数y=log3x(x>1)的图象在函数y=log6x(x>1)的图象的上方,故log35>log65.
(3)把lg
m看作指数函数y=ax(a>0,且a≠1)的底数,要比较两数的大小,关键是比较底数lg
m与1的关系.若lg
m>1,即m>10,则y=(lg
m)x在R上是增函数,故(lg
m)1.9<(lg
m)2.1;若0<lg
m<1,即1<m<10,则y=(lg
m)x在R上是减函数,故(lg
m)1.9>(lg
m)2.1;若lg
m=1,即m=10,则(lg
m)1.9=(lg
m)2.1.
(4)因为底数8,10均大于1,且10>8,
所以log85>lg
5>lg
4,即log85>lg
4.点评
本题代表了几个典型的题型.其中题(1)是直接利用对数函数的单调性;题(2)是对数函数的底数变化规律的应用;题(3)是指数函数的单调性及对数函数性质的综合运用;题(4)是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的增减性.常用的中间量有0,1等,可通过估算加以选择.
探究四
求复合函数的单调区间
求复合函数的单调区间的步骤:1.求出函数的定义域;
2.将复合函数分解为基本初等函数;
3.分别确定各个基本初等函数的单调性;
4.根据复合函数原理求出复合函数的单调区间.
【典型例题4】求下列函数的单调区间:
(1)y=log0.2(x2-2x+2);
(2)y=loga(a-ax).
思路分析:利用复合函数法确定其单调区间即可.
解:(1)令u=x2-2x+2=(x-1)2+1≥1>0.
当x≥1时,u=x2-2x+2是增函数,
又y=log0.2u是减函数,
所以y=log0.2(x2-2x+2)在[1,+∞)上是减函数.
同理可得函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1].故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],单调减区间为[1,+∞).
(2)①当a>1时,y=logat是增函数,且t=a-ax是减函数,而a-ax>0,即ax所以y=loga(a-ax)在(-∞,1)上是减函数.
②当00,即ax所以y=loga(a-ax)在(-∞,1)上是增函数.
综上所述,当a>1时,函数y=loga(a-ax)在(-∞,1)上是减函数;当0探究五
易错辨析
易错点 忽视真数的取值范围而致误
【典型例题5】解不等式loga(2x-5)>loga(x-1).
错解一:由2x-5>x-1,得x>4,故原不等式的解集为{x|x>4}.
错解二:由
解得x>4,
故原不等式的解集为{x|x>4}.
错解三:原不等式可等价变形为
解得x>4.
所以当a>1时,原不等式的解集为{x|x>4};
当0错因分析:错解一中没考虑真数的取值范围,也没有对a进行分类讨论;错解二中没有对a进行分类讨论;错解三中出现逻辑性错误,运算变形的顺序出现了问题,即开始默认了a>1对原不等式进行了转化是不正确的,虽然后来对a又进行了讨论,看起来结果正确.
正解:当a>1时,原不等式等价于
解得x>4.
当0解得综上,当a>1时,原不等式的解集为{x|x>4};
当0
探究一
求对数函数的定义域
求对数函数定义域的步骤
【典型例题1】(1)函数f(x)=+ln(4-x)的定义域为( )
A.[-1,4)
B.(-1,+∞)
C.(-1,4)
D.(4,+∞)
(2)函数y=loga
(a>0,a≠1)的定义域为__________.
解析:(1)由题意可知解得x∈[-1,4),故选A.
(2)由题意可得>0,又∵偶次根号下非负,∴x-1>0,即x>1.
∴函数y=loga
(a>0,a≠1)的定义域为(1,+∞).
答案:(1)A (2)(1,+∞)
探究二
对数函数的图象
对数函数图象的变化规律:
1.对于几个底数都大于1的对数函数,底数越大,函数图象向右的方向越接近x轴;对于几个底数都大于0且小于1的对数函数,底数越大,函数图象向右的方向越远离x轴.以上规律可总结成x>1时“底大图低”.实际上,作出直线y=1,它与各图象交点的横坐标即为各函数的底数的大小,如图所示.
2.当a>1时,图象向下无限接近于y轴;当0
【典型例题2】
函数y=log2x,y=log5x,y=lg
x的图象如图所示.
(1)说明哪个函数对应于哪个图象,并解释为什么;
(2)在如图的平面直角坐标系中分别画出y=,y=,y=的图象;
(3)从(2)的图中你发现了什么?
解:(1)①对应函数y=lg
x,②对应函数y=log5x,③对应函数y=log2x.这是因为当底数全大于1时,在x=1时右侧,底数越大的函数图象越靠近x轴.
(2)在题图中的平面直角坐标系中分别画出y=,y=,y=的图象如图所示.
(3)从(2)的图中可以发现:y=lg
x与y=,y=log5x与y=,y=log2x与y=分别关于x轴对称.
探究三
利用对数函数的性质比较大小
1.如果两个对数的底数相同,则由对数函数的单调性(当底数a>1时,函数为增函数;当底数0
(1)当a1>a2>1时,根据对数函数图象的变化规律知当x>1时,y1
对于含有参数的两个对数值的大小比较,要注意根据对数的底数是否大于1进行分类讨论.
【典型例题3】比较大小:
(1)log0.27与log0.29;
(2)log35与log65;
(3)(lg
m)1.9与(lg
m)2.1(m>1);
(4)log85与lg
4.
解:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两个函数值,由y=log0.2x在(0,+∞)上是减函数,得log0.27>log0.29.
(2)函数y=log3x(x>1)的图象在函数y=log6x(x>1)的图象的上方,故log35>log65.
(3)把lg
m看作指数函数y=ax(a>0,且a≠1)的底数,要比较两数的大小,关键是比较底数lg
m与1的关系.若lg
m>1,即m>10,则y=(lg
m)x在R上是增函数,故(lg
m)1.9<(lg
m)2.1;若0<lg
m<1,即1<m<10,则y=(lg
m)x在R上是减函数,故(lg
m)1.9>(lg
m)2.1;若lg
m=1,即m=10,则(lg
m)1.9=(lg
m)2.1.
(4)因为底数8,10均大于1,且10>8,
所以log85>lg
5>lg
4,即log85>lg
4.点评
本题代表了几个典型的题型.其中题(1)是直接利用对数函数的单调性;题(2)是对数函数的底数变化规律的应用;题(3)是指数函数的单调性及对数函数性质的综合运用;题(4)是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的增减性.常用的中间量有0,1等,可通过估算加以选择.
探究四
求复合函数的单调区间
求复合函数的单调区间的步骤:1.求出函数的定义域;
2.将复合函数分解为基本初等函数;
3.分别确定各个基本初等函数的单调性;
4.根据复合函数原理求出复合函数的单调区间.
【典型例题4】求下列函数的单调区间:
(1)y=log0.2(x2-2x+2);
(2)y=loga(a-ax).
思路分析:利用复合函数法确定其单调区间即可.
解:(1)令u=x2-2x+2=(x-1)2+1≥1>0.
当x≥1时,u=x2-2x+2是增函数,
又y=log0.2u是减函数,
所以y=log0.2(x2-2x+2)在[1,+∞)上是减函数.
同理可得函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1].故函数y=log0.2(x2-2x+2)的单调增区间为(-∞,1],单调减区间为[1,+∞).
(2)①当a>1时,y=logat是增函数,且t=a-ax是减函数,而a-ax>0,即ax
②当0
综上所述,当a>1时,函数y=loga(a-ax)在(-∞,1)上是减函数;当0
易错辨析
易错点 忽视真数的取值范围而致误
【典型例题5】解不等式loga(2x-5)>loga(x-1).
错解一:由2x-5>x-1,得x>4,故原不等式的解集为{x|x>4}.
错解二:由
解得x>4,
故原不等式的解集为{x|x>4}.
错解三:原不等式可等价变形为
解得x>4.
所以当a>1时,原不等式的解集为{x|x>4};
当0
正解:当a>1时,原不等式等价于
解得x>4.
当0
当0
