11.3.1 多边形课件
图片预览






文档简介
课件42张PPT。 多边形 1学习目标1、知道多边形的概念;
2、会探究多边形对角线的条数。
教学重难点:重点:多边形的对角线及内角和与外角和
和正多边形的概念
难点:多边形对角线的总条数内角和与外角和的应用自主学习:
预习教材141~146页,并完成导学案上的自学预检3.学会用三角形内角和定理证明多边形的内角和与外角和;
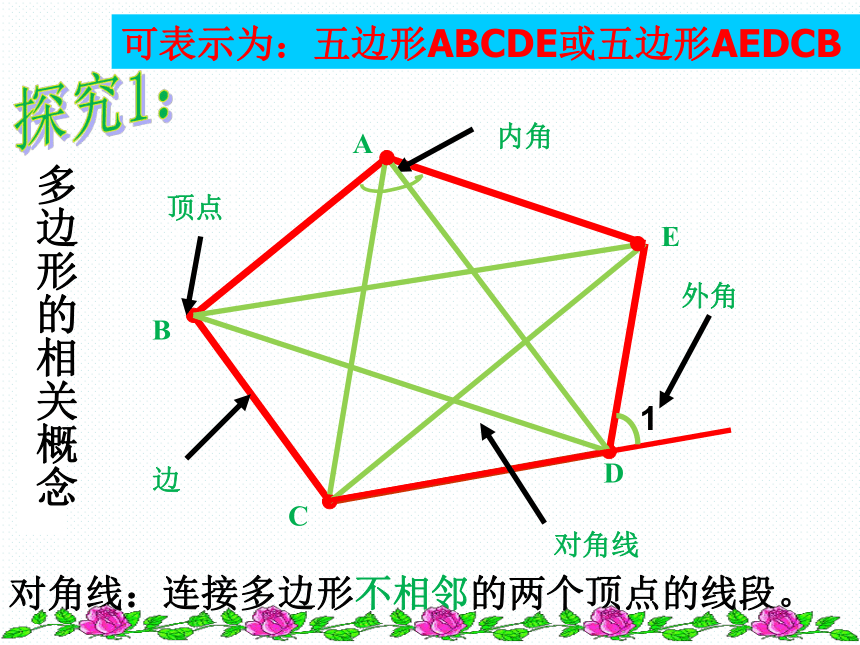
4.会利用多边形的内角和与外角和来解决相关问题。 在同一平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。……五边形六边形七边形 在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形多边形的定义: 多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。 如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。内角对角线对角线:连接多边形不相邻的两个顶点的线段。可表示为:五边形ABCDE或五边形AEDCBABCDE外角1
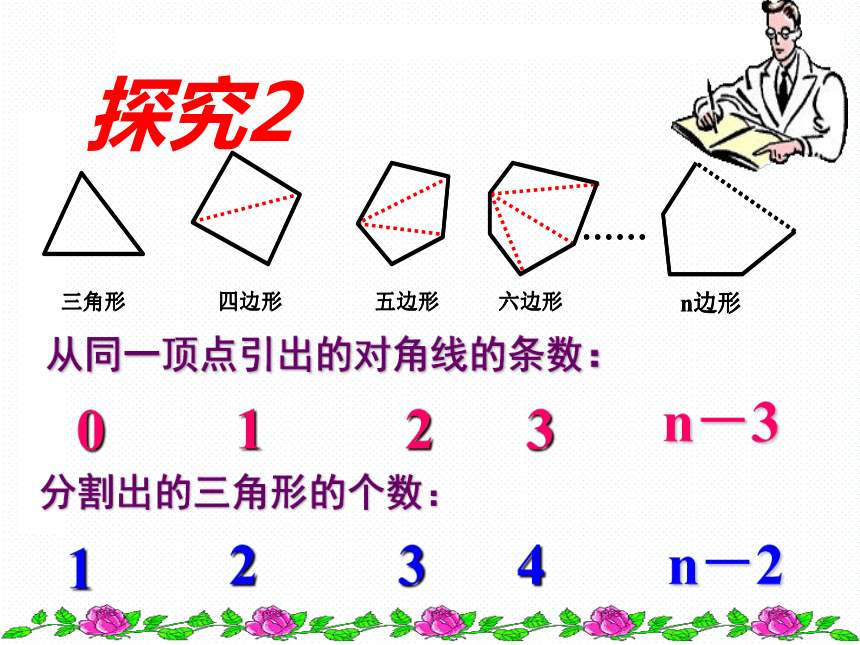
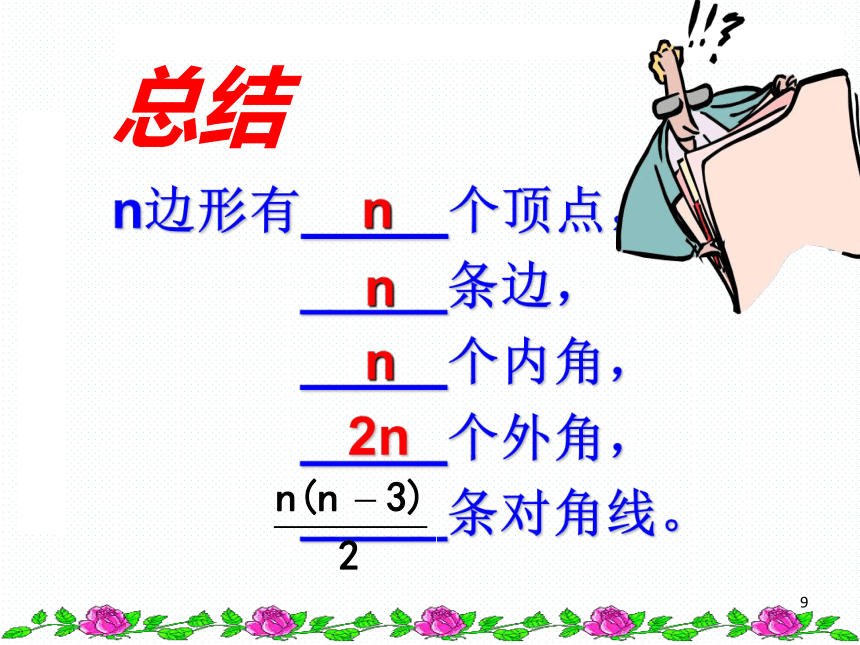
探究1:多边形的相关概念顶点边 连结多边形不相邻的两个顶点的线段,叫做多边形的对角线。 请说出下列图形从某一顶点出发的对角线的条数:多边形的对角线从同一顶点引出的对角线的条数:123n-3分割出的三角形的个数:234n-201探究2 n边形从一个顶点出发的对角线条数为: 条(n≥3),把多边形分成________个三角形n边形共有对角线 条(n≥3)(n-3)总结(n-2)1n边形有_____个顶点,
_____条边,
_____个内角,
_____个外角,
_____条对角线。nnn2n总结三角形的外角与内角的关系: 1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的两个内角的和;
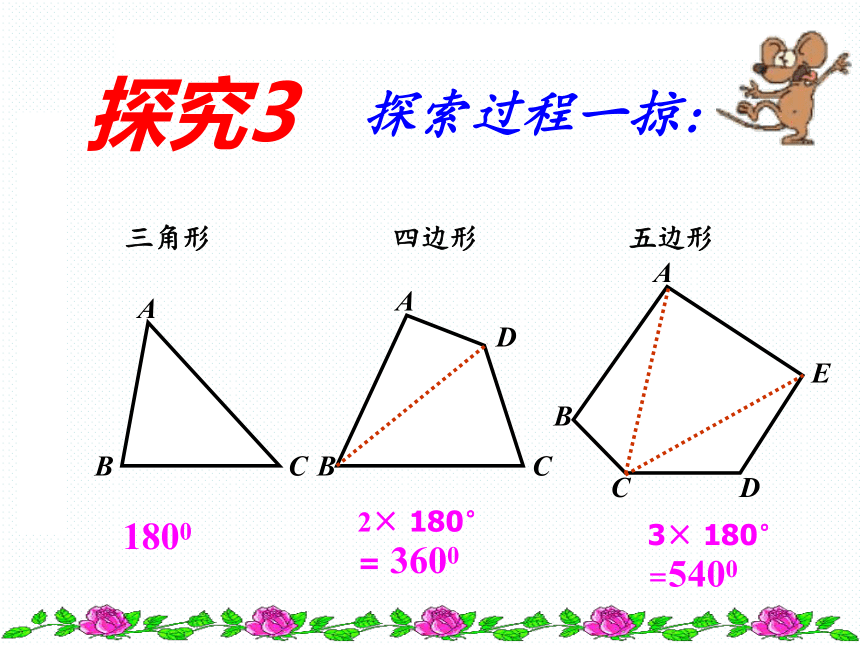
3、三角形的一个外角 任何一个与它不相邻的内角。等于大于互补复习回顾 三角形 四边形 五边形 1800 2× 180°
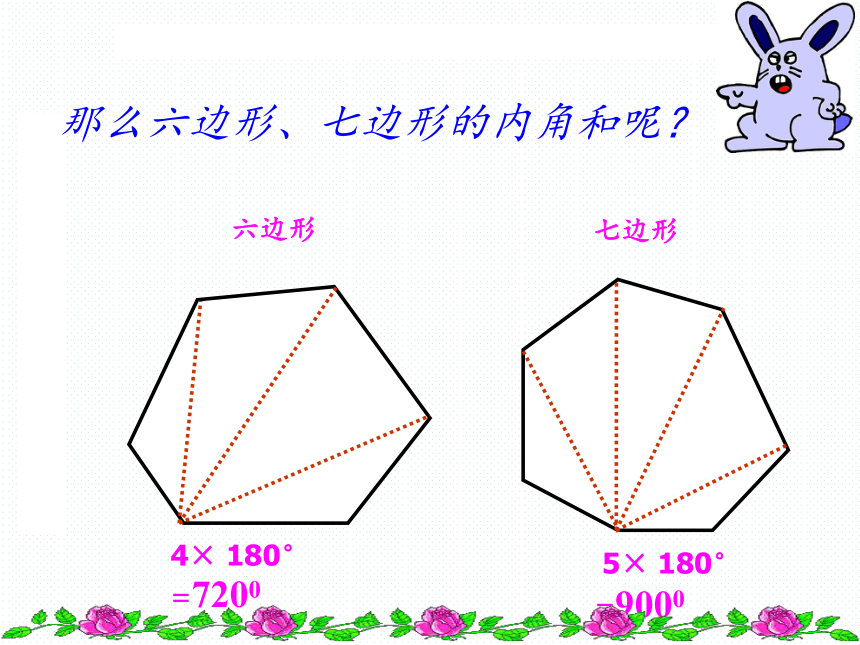
= 3600 3× 180° =5400 探索过程一掠:探究3六边形 七边形4× 180° =7200 5× 180° =9000 那么六边形、七边形的内角和呢?………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内角和的? 从多边形的一个顶点出发,把一个多边形分成几个三角形.E
ABCDO180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)解:如图四边形ABCD中,例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?这就是说,如果四边形的一组对角互补,那么另一组对角也互补。典型例题2、已知一个多边形每个内角都等108° ,求这个多边形的边数?解:设这个多边形的边数为 n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。1、八边形的内角和等于多少度? 十边形呢?(8-2) ×180°= 1080°(10-2) ×180°= 1440°小试牛刀3、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720o,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。1800°180°六十 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少? 61.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?探究4五边形外角和结论:五边形的外角和等于360°-(5-2) × 180°=360 °=5个平角-5边形内角和=5×180° 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少? 例2 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形的外角和等于多少?n边形外角和结论:
n边形的外角和等于360°-(n-2) × 180°=360 °= n个平角-n边形内角和=n×180 °例3、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?练一练练习1: 如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.12∴n×30°=360°n=12解:∵n边形外角和=360 ° 练习2. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6. 如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。多边形的分类 四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧。 正方形的各个角都相等,各条边都相等。
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.例如:正三角形正方形正五边形正六边形正多边形那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢? ……
正n边形(5-2)×180°
5
=108°(6-2)×180°
6
=120°(8-2)×180°
8
=135°(n-2)×180°
n 1、正多边形的内角探究5回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是2、正多边形的外角例1:一个正多边形的一个内角为150°,你知道它是几边形吗? 解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。典型例题 例2:正五边形的每一个外角等于____,每一个内角等于_____。5x=360°x=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °例3:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。通过这节课的学习你有哪些收获?还有什么疑惑?感悟与反思有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。内角和减少180O内角和不变内角和增加180O知识拓展3、n边形的内角和为 (n≥3)1、n边形从一个顶点出发的对角线有 条(n≥3)4、任何多边形的外角和为课堂小结5. 已知内角和求几边形:6、正n边形每个内角的度数是 7、正n边形每个外角的度数是 (n-2)×180°
n(n-3)(n-2) ×180°360°内角和÷180+21.七边形的外角和是____;十二边形的外角和是______;三角形的外角和是__.
2.一个多边形的每一个外角都等于36°则这个多边形是_______边形.
3.在每个内角都相等的多边形中,若一个外角是它相邻内角的 ,则这个多边形是______边形.
4.一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是_____.
5如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别____.
达标检测题6.n边形的内角和等于____,九 边形的内角和等于______.
7.如果一个多边形的内角和是1440度,那么这是____边形.
8.已知多边形的每个内角都等于150°,求这个多边形的边数?
9.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
10.若一个多边形的内角和为1080°,则它的边数是______. 达标检测题 11.当一个多边形的边数增加1时,它的内角和增加_________度.
12._______边形的内角和与外角和相等.
13.已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.
14.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
15.若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。达标检测题
2、会探究多边形对角线的条数。
教学重难点:重点:多边形的对角线及内角和与外角和
和正多边形的概念
难点:多边形对角线的总条数内角和与外角和的应用自主学习:
预习教材141~146页,并完成导学案上的自学预检3.学会用三角形内角和定理证明多边形的内角和与外角和;
4.会利用多边形的内角和与外角和来解决相关问题。 在同一平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。……五边形六边形七边形 在平面内,由一些线段首位顺次相接组成的封闭图形叫做多边形多边形的定义: 多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。 如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。内角对角线对角线:连接多边形不相邻的两个顶点的线段。可表示为:五边形ABCDE或五边形AEDCBABCDE外角1
探究1:多边形的相关概念顶点边 连结多边形不相邻的两个顶点的线段,叫做多边形的对角线。 请说出下列图形从某一顶点出发的对角线的条数:多边形的对角线从同一顶点引出的对角线的条数:123n-3分割出的三角形的个数:234n-201探究2 n边形从一个顶点出发的对角线条数为: 条(n≥3),把多边形分成________个三角形n边形共有对角线 条(n≥3)(n-3)总结(n-2)1n边形有_____个顶点,
_____条边,
_____个内角,
_____个外角,
_____条对角线。nnn2n总结三角形的外角与内角的关系: 1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的两个内角的和;
3、三角形的一个外角 任何一个与它不相邻的内角。等于大于互补复习回顾 三角形 四边形 五边形 1800 2× 180°
= 3600 3× 180° =5400 探索过程一掠:探究3六边形 七边形4× 180° =7200 5× 180° =9000 那么六边形、七边形的内角和呢?………………34567n1n-22345180°360°540°720°900°(n-2) ·180°(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和=(n-2) ·180°反思:我们是怎样求多边形内角和的? 从多边形的一个顶点出发,把一个多边形分成几个三角形.E
ABCDO180°× 5 – 360°= 540°180°× 5=900°?五边形内角和540°??把一个五边形分成几个三角形,还有其他的分法吗?ABCDEF180° × 4 – 180° = 540°三角形六边形四边形八边形……..五边形是解决多边形问题的常用辅助线 对角线多边形问题 三角形问题转化(未知)(已知)解:如图四边形ABCD中,例1、如果一个四边形的一组对角互补,那么另一组对角有什么关系?这就是说,如果四边形的一组对角互补,那么另一组对角也互补。典型例题2、已知一个多边形每个内角都等108° ,求这个多边形的边数?解:设这个多边形的边数为 n,根据题意得:
(n-2) ×180=108n
解得:n=5 答:这个多边形是五边形。1、八边形的内角和等于多少度? 十边形呢?(8-2) ×180°= 1080°(10-2) ×180°= 1440°小试牛刀3、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720o,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。1800°180°六十 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少? 61.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?探究4五边形外角和结论:五边形的外角和等于360°-(5-2) × 180°=360 °=5个平角-5边形内角和=5×180° 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少? 例2 在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形的外角和等于多少?n边形外角和结论:
n边形的外角和等于360°-(n-2) × 180°=360 °= n个平角-n边形内角和=n×180 °例3、已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?练一练练习1: 如果一个多边形的每一个外角等于30°,则这个多边形的边数是_____.12∴n×30°=360°n=12解:∵n边形外角和=360 ° 练习2. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数.解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6. 如图,画出四边形ABCD的任何一条边所在直线,整个四边形都在这条直线的同一侧,这样的四边形叫做凸四边形。多边形的分类 四边形ABCD是凹四边形,因为画出边CD(或BC)所在直线,整个四边形不都在这条直线的同一侧。 正方形的各个角都相等,各条边都相等。
像正方形这样,各个角都相等,各条边都相等的多边形叫做正多边形.例如:正三角形正方形正五边形正六边形正多边形那么正五边形、正六边形、正八边形、正n边形的每个内角分别是多少度呢? ……
正n边形(5-2)×180°
5
=108°(6-2)×180°
6
=120°(8-2)×180°
8
=135°(n-2)×180°
n 1、正多边形的内角探究5回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是2、正多边形的外角例1:一个正多边形的一个内角为150°,你知道它是几边形吗? 解:设 这个多边形为n边形,根据题意得:
(n-2)×180=150n
n=12
答:这个多边形是12边形。另解:由于多边形外角和等于360°
而这个正多边形的每个外角都等于
180°-150°=30°,
所以这个正 多边形的边数等于
360°÷30°=12。典型例题 例2:正五边形的每一个外角等于____,每一个内角等于_____。5x=360°x=72°72°108°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °例3:一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。 解:设一个外角为x°,
则内角为(x+36)°
根据题意得:
x+x+36=180
x=72
360÷72=5
答:这个正多边形为正五边形。通过这节课的学习你有哪些收获?还有什么疑惑?感悟与反思有一六边形,截去一三角形,内角和会发生
怎样变化?请画图说明。内角和减少180O内角和不变内角和增加180O知识拓展3、n边形的内角和为 (n≥3)1、n边形从一个顶点出发的对角线有 条(n≥3)4、任何多边形的外角和为课堂小结5. 已知内角和求几边形:6、正n边形每个内角的度数是 7、正n边形每个外角的度数是 (n-2)×180°
n(n-3)(n-2) ×180°360°内角和÷180+21.七边形的外角和是____;十二边形的外角和是______;三角形的外角和是__.
2.一个多边形的每一个外角都等于36°则这个多边形是_______边形.
3.在每个内角都相等的多边形中,若一个外角是它相邻内角的 ,则这个多边形是______边形.
4.一个多边形的每一个外角都等于40°,则它的边数是__________;一个多边形的每一个内角都等于140°,则它的边数是_____.
5如果四边形有一个角是直角,另外三个角的度数之比为2:3:4,那么这三个内角的度数分别____.
达标检测题6.n边形的内角和等于____,九 边形的内角和等于______.
7.如果一个多边形的内角和是1440度,那么这是____边形.
8.已知多边形的每个内角都等于150°,求这个多边形的边数?
9.一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A.360° B.540° C.720° D.900°
10.若一个多边形的内角和为1080°,则它的边数是______. 达标检测题 11.当一个多边形的边数增加1时,它的内角和增加_________度.
12._______边形的内角和与外角和相等.
13.已知一个多边形的内角和与外角和的差为1080°,则这个多边形是_____边形.
14.已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
15.若一个多边形的内角和与外角和的比为7:2,求这个多边形的边数。达标检测题
