人教A版数学必修四1.2.1 任意角的三角函数 课件 (共35张PPT)
文档属性
| 名称 | 人教A版数学必修四1.2.1 任意角的三角函数 课件 (共35张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 340.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-19 00:00:00 | ||
图片预览



文档简介
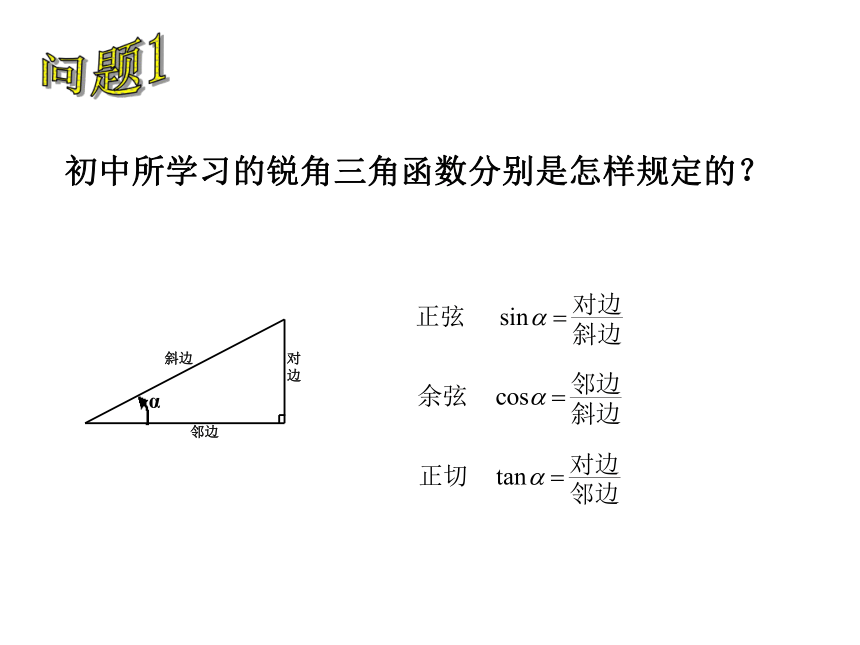
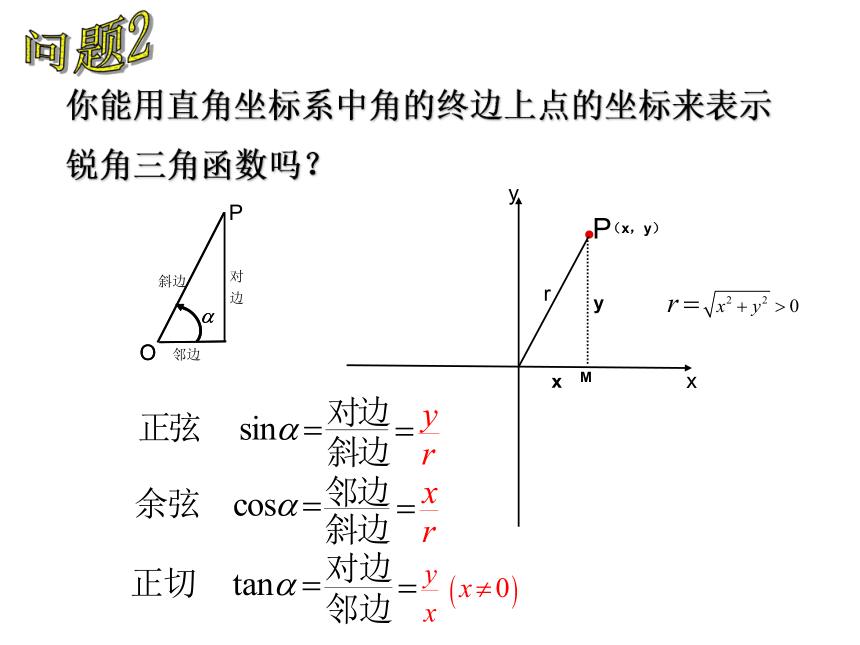
课件35张PPT。1.2.1 任意角的三角函数初中所学习的锐角三角函数分别是怎样规定的?问题1ry x (x,y)M问题2你能用直角坐标系中角的终边上点的坐标来表示
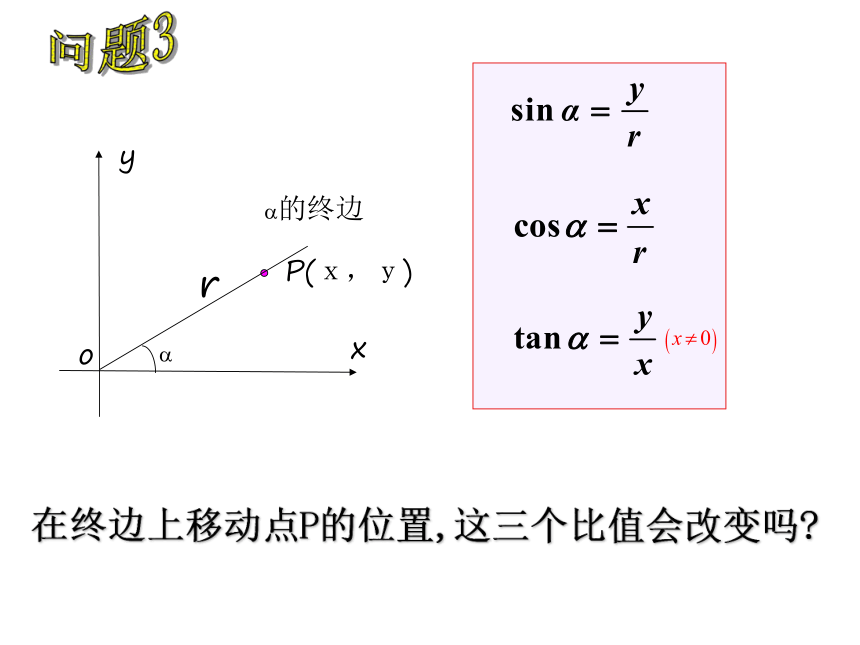
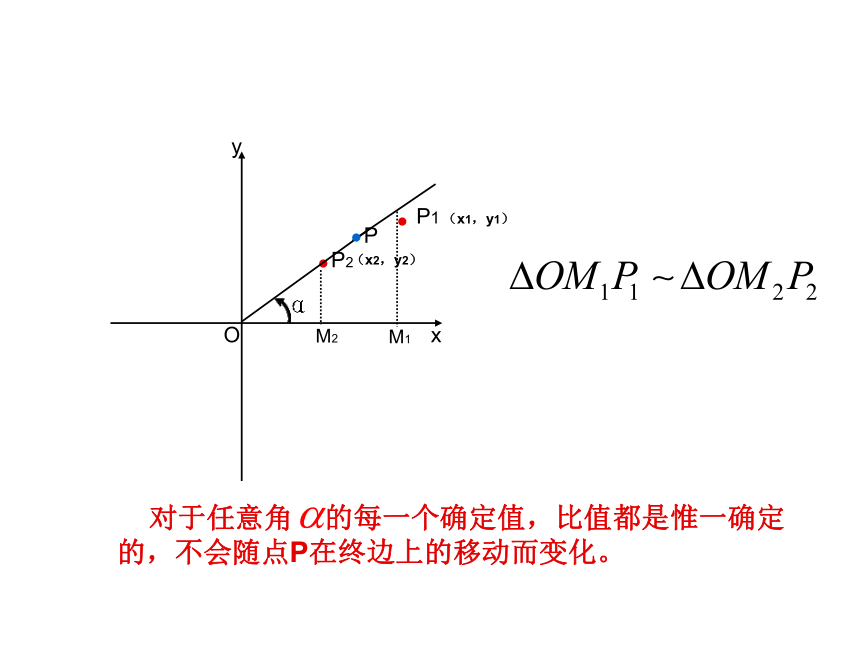
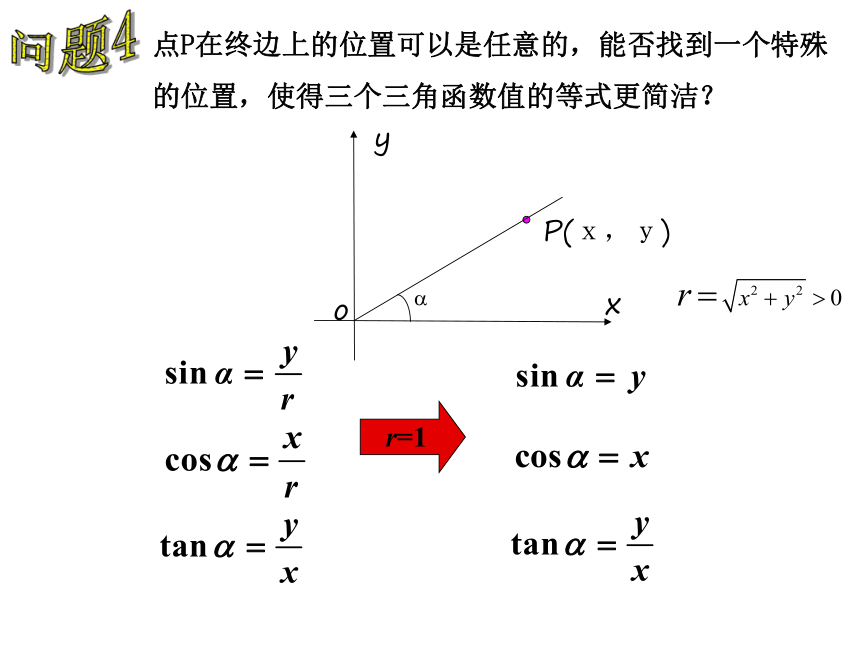
锐角三角函数吗?P(x,y)?的终边 r?在终边上移动点P的位置,这三个比值会改变吗?问题3M1M2P(x,y)?r=1问题4点P在终边上的位置可以是任意的,能否找到一个特殊
的位置,使得三个三角函数值的等式更简洁? 在直角坐标系中,以原点O为
圆心,以单位长度为半径的圆
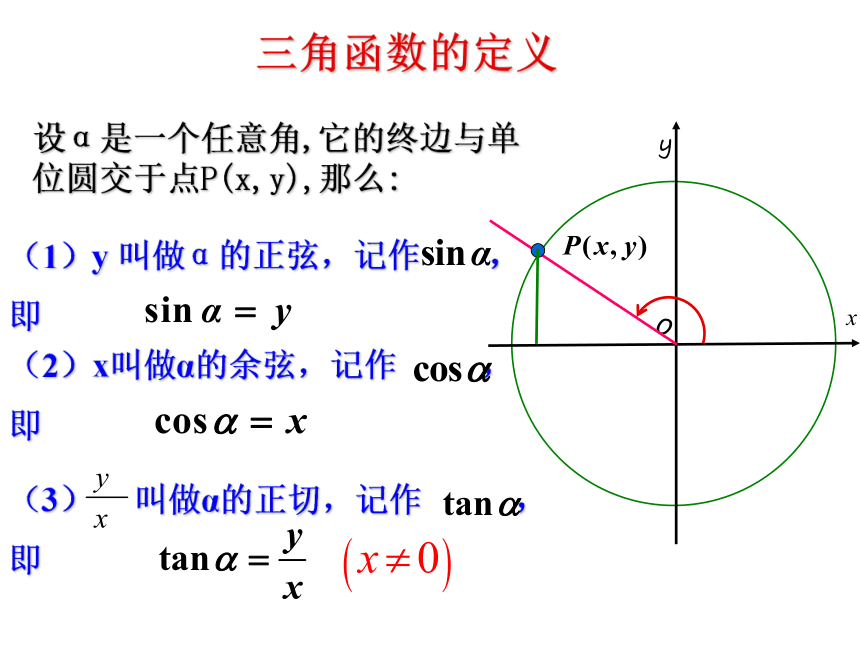
为单位圆。锐角三角函数可以用单位圆上的点的坐标来表示。单位圆xyoyxO设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:(1)y 叫做α的正弦,记作 ,
即(2)x叫做α的余弦,记作 ,
即(3) 叫做α的正切,记作 ,
即三角函数的定义正弦、余弦、正切都是以角为自变量,以单位圆
上的点的坐标或坐标的比值为函数值的函数,统
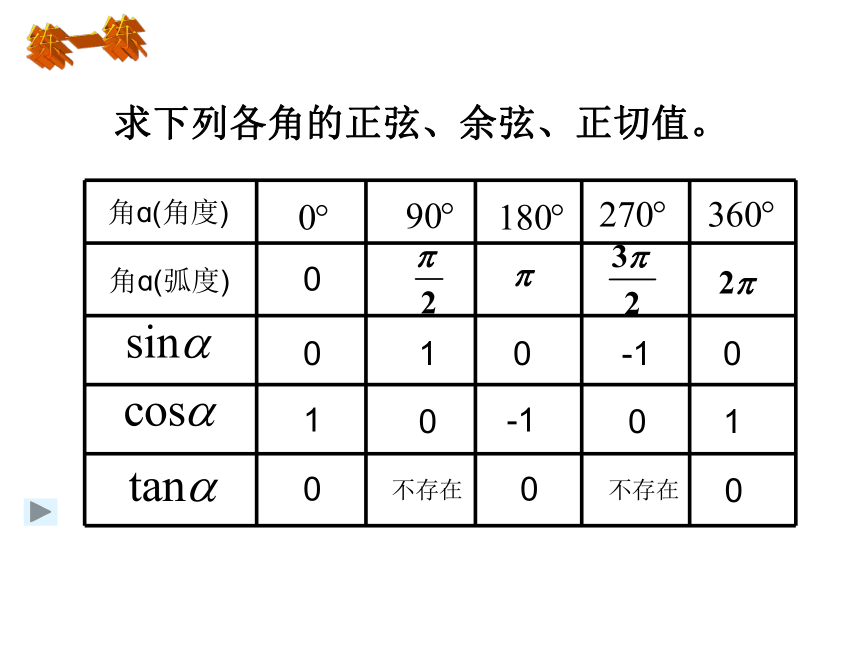
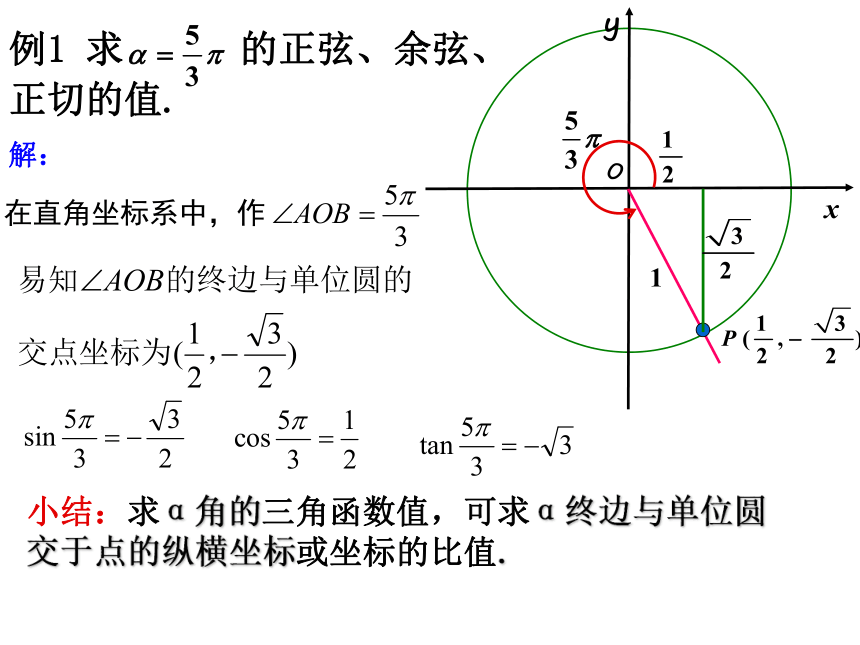
称它们为三角函数。求下列各角的正弦、余弦、正切值。练一练例1 求 的正弦、余弦、
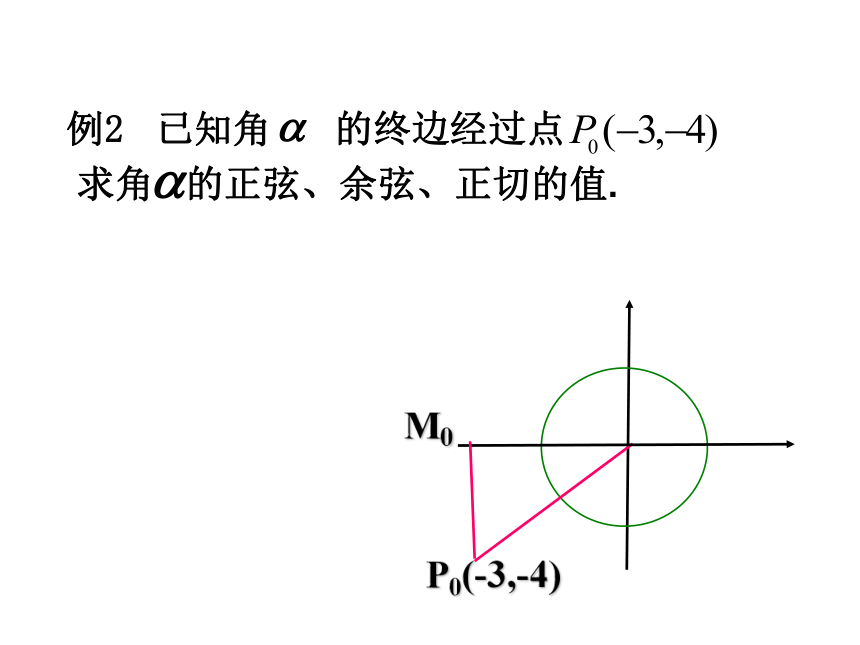
正切的值.yxO小结:求α角的三角函数值,可求α终边与单位圆交于点的纵横坐标或坐标的比值.解:例2 已知角 的终边经过点
求角 的正弦、余弦、正切的值.P(x,y)?的终边 r?三角函数也可定义为:设α是一个任意角,它的终边经过点P(x,y),则( ) 三角函数的定义域:RR探究 ( )+ + - - ++ - -+ +--函数值在各象限的符号练习:判断下列三角函数值的符号:
例3 求证:当下列不等式组成立时,角 为第三象限角.反之也成立根据三角函数的定义,终边相同的角的同一三角函数值相等?
终边相同点的坐标相同同一函数值相同终边相同的角的同一三角函数值相等!问题5与?终边相同的角可以表示为: 练习:求下列三角函数值:
与单位圆有关的有向线段MP、OM、AT分别称为正弦线、
余弦线、正切线,统称为三角函数线。三角函数线探究:角α与2kπ+α(k∈Z)的同名三角函数值大小有何关系?为什么?即: sinα与 sin(2kπ+α),
cosα与 cos(2kπ+α),
tanα与 tan(2kπ+α). sin(2kπ+α)= sinα,
cos(2kπ+α)= cosα,
tan(2kπ+α)= tanα, 其中k∈Z. 公式一(诱导公式一): 提问:你能用文字语言怎样描述公式一吗?有何作用?终边相同的角的同一三角函数的值相等 作用:利用公式一,可以把求任意角的三角函数值都转化为求0~2?(或0o~360o)角的三角函数值。
公式一从代数的角度揭示了三角函数值的周期变化规律,即“角的终边绕原点每转动一周,函数值都重复出现”。例4、确定下列三角函数值的符号:例5、求下列三角函数值:
练习:
(见P15练习5、7) 设任意角?顶点在原点O,始边与x轴非负半轴重合,终边与单位圆相交与点P(x,y),过P作x轴的垂线,垂足为M;过点A(1,0)作单位圆的切线,它与角?的终边或其反向延长线交与点T.规定:与坐标轴方向一致时为正,与坐标方向相反时为负.有向线段:规定了方向的线段.有向线段AB:方向A→B;记作
有向线段BA:方向B→A ;记作
有向线段CD:方向C→D,等.值为正值为负探究:能否去掉绝对值符号,使得线段OM,MP的值与的正负是一致呢?怎样规定? 有向线段的书写: 有向线段的起点字母在前,终点字母在后面.有向线段MP:方向M→P,方向与y轴的正方向一致,
其值为正,即MP=|MP|>0;
有向线段PM:方向P→M,方向与y轴的正方向相反,
其值为负,即PM= - |MP|<0;
有向线段OM:方向O→M,方向与x轴的正方向一致,
其值为正,即OM=|OM|>0.三角函数线定义有向线段MP、OM、AT分别称为正弦线、余弦线、正切线.统称为三角函数线.(它是三角函数值的一种几何表示法)说明:
① 三条有向线段的位置:正弦线为?的终边与单位圆的交点到x轴的垂直线段;余弦线在x轴上;正切线在过单位圆与x轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
② 三条有向线段的方向:正弦线由垂足指向?的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与?的终边的交点。
③ 三条有向线段的正负:三条有向线段凡与x轴或y轴同向的为正值,与x轴或y轴反向的为负值。选讲下列各式为正号的是( )
A cos2-sin2 B cos2?sin2
C tan2?sec2 D sin2?tan2C2 若lg(sin??tan?)有意义,则?是( )
A 第一象限角 B 第四象限角
C 第一象限角或第四象限角
D 第一或第四象限角或x轴的正半轴C3 已知?的终边过点(3a-9,a+2),且cos??0,
sin?>0,则a的取值范围是 。-2 且|cos(?/2)|=- cos(?/2),
问?/2是第几象限角?练习 已知?是第三象限角,且sin(?/2)<0,
则( )
A cos(?/2)<0 B cos(?/2)>0
C tan(?/2)>0 D cot(?/2)>0B(1).单位圆定义任意角的三角函数;
(2).由终边上任一点求任意角的三角函数;
(3).各象限的符号情况.
(4).利用诱导公式一求三角函数值
(5).三角函数线的定义,会画任意角的三角函数线;
(6).利用单位圆比较三角函数值的大小,求角的范围。本节主要知识:小结:(1)任意角的三角函数定义
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:定义域为R定义域为R定义域为小结3.公式一(诱导公式)应用(1)判断符号(2)求值 ( )++--++--++--小结三角函数在各象限内的符号
锐角三角函数吗?P(x,y)?的终边 r?在终边上移动点P的位置,这三个比值会改变吗?问题3M1M2P(x,y)?r=1问题4点P在终边上的位置可以是任意的,能否找到一个特殊
的位置,使得三个三角函数值的等式更简洁? 在直角坐标系中,以原点O为
圆心,以单位长度为半径的圆
为单位圆。锐角三角函数可以用单位圆上的点的坐标来表示。单位圆xyoyxO设α是一个任意角,它的终边与单位圆交于点P(x,y),那么:(1)y 叫做α的正弦,记作 ,
即(2)x叫做α的余弦,记作 ,
即(3) 叫做α的正切,记作 ,
即三角函数的定义正弦、余弦、正切都是以角为自变量,以单位圆
上的点的坐标或坐标的比值为函数值的函数,统
称它们为三角函数。求下列各角的正弦、余弦、正切值。练一练例1 求 的正弦、余弦、
正切的值.yxO小结:求α角的三角函数值,可求α终边与单位圆交于点的纵横坐标或坐标的比值.解:例2 已知角 的终边经过点
求角 的正弦、余弦、正切的值.P(x,y)?的终边 r?三角函数也可定义为:设α是一个任意角,它的终边经过点P(x,y),则( ) 三角函数的定义域:RR探究 ( )+ + - - ++ - -+ +--函数值在各象限的符号练习:判断下列三角函数值的符号:
例3 求证:当下列不等式组成立时,角 为第三象限角.反之也成立根据三角函数的定义,终边相同的角的同一三角函数值相等?
终边相同点的坐标相同同一函数值相同终边相同的角的同一三角函数值相等!问题5与?终边相同的角可以表示为: 练习:求下列三角函数值:
与单位圆有关的有向线段MP、OM、AT分别称为正弦线、
余弦线、正切线,统称为三角函数线。三角函数线探究:角α与2kπ+α(k∈Z)的同名三角函数值大小有何关系?为什么?即: sinα与 sin(2kπ+α),
cosα与 cos(2kπ+α),
tanα与 tan(2kπ+α). sin(2kπ+α)= sinα,
cos(2kπ+α)= cosα,
tan(2kπ+α)= tanα, 其中k∈Z. 公式一(诱导公式一): 提问:你能用文字语言怎样描述公式一吗?有何作用?终边相同的角的同一三角函数的值相等 作用:利用公式一,可以把求任意角的三角函数值都转化为求0~2?(或0o~360o)角的三角函数值。
公式一从代数的角度揭示了三角函数值的周期变化规律,即“角的终边绕原点每转动一周,函数值都重复出现”。例4、确定下列三角函数值的符号:例5、求下列三角函数值:
练习:
(见P15练习5、7) 设任意角?顶点在原点O,始边与x轴非负半轴重合,终边与单位圆相交与点P(x,y),过P作x轴的垂线,垂足为M;过点A(1,0)作单位圆的切线,它与角?的终边或其反向延长线交与点T.规定:与坐标轴方向一致时为正,与坐标方向相反时为负.有向线段:规定了方向的线段.有向线段AB:方向A→B;记作
有向线段BA:方向B→A ;记作
有向线段CD:方向C→D,等.值为正值为负探究:能否去掉绝对值符号,使得线段OM,MP的值与的正负是一致呢?怎样规定? 有向线段的书写: 有向线段的起点字母在前,终点字母在后面.有向线段MP:方向M→P,方向与y轴的正方向一致,
其值为正,即MP=|MP|>0;
有向线段PM:方向P→M,方向与y轴的正方向相反,
其值为负,即PM= - |MP|<0;
有向线段OM:方向O→M,方向与x轴的正方向一致,
其值为正,即OM=|OM|>0.三角函数线定义有向线段MP、OM、AT分别称为正弦线、余弦线、正切线.统称为三角函数线.(它是三角函数值的一种几何表示法)说明:
① 三条有向线段的位置:正弦线为?的终边与单位圆的交点到x轴的垂直线段;余弦线在x轴上;正切线在过单位圆与x轴正方向的交点的切线上,三条有向线段中两条在单位圆内,一条在单位圆外。
② 三条有向线段的方向:正弦线由垂足指向?的终边与单位圆的交点;余弦线由原点指向垂足;正切线由切点指向与?的终边的交点。
③ 三条有向线段的正负:三条有向线段凡与x轴或y轴同向的为正值,与x轴或y轴反向的为负值。选讲下列各式为正号的是( )
A cos2-sin2 B cos2?sin2
C tan2?sec2 D sin2?tan2C2 若lg(sin??tan?)有意义,则?是( )
A 第一象限角 B 第四象限角
C 第一象限角或第四象限角
D 第一或第四象限角或x轴的正半轴C3 已知?的终边过点(3a-9,a+2),且cos??0,
sin?>0,则a的取值范围是 。-2
问?/2是第几象限角?练习 已知?是第三象限角,且sin(?/2)<0,
则( )
A cos(?/2)<0 B cos(?/2)>0
C tan(?/2)>0 D cot(?/2)>0B(1).单位圆定义任意角的三角函数;
(2).由终边上任一点求任意角的三角函数;
(3).各象限的符号情况.
(4).利用诱导公式一求三角函数值
(5).三角函数线的定义,会画任意角的三角函数线;
(6).利用单位圆比较三角函数值的大小,求角的范围。本节主要知识:小结:(1)任意角的三角函数定义
三角函数(正弦,余弦,正切)都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数.
(由于角的集合与实数集合之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.)
所以三角函数可以记为:定义域为R定义域为R定义域为小结3.公式一(诱导公式)应用(1)判断符号(2)求值 ( )++--++--++--小结三角函数在各象限内的符号
