人教版高中数学A版必修四2.2.1向量加法运算及其几何意义教学课件 (共69张PPT)
文档属性
| 名称 | 人教版高中数学A版必修四2.2.1向量加法运算及其几何意义教学课件 (共69张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 326.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-19 09:57:30 | ||
图片预览




文档简介
课件69张PPT。2.2.1向量加法运算
及其几何意义
1、什么叫向量? 2、什么叫共线向量?既有大小又有方向的量叫向量
方向相同或相反的非零向量叫共线向量3、什么叫相等向量?长度相等且方向相同的向量叫相等向量。
也叫平行向量回顾旧知问题
数可进行加法运算:1+2=3 .那
么向量的加法是怎样定义的?长度是1
的向量与长度是2的向量相加是否一定
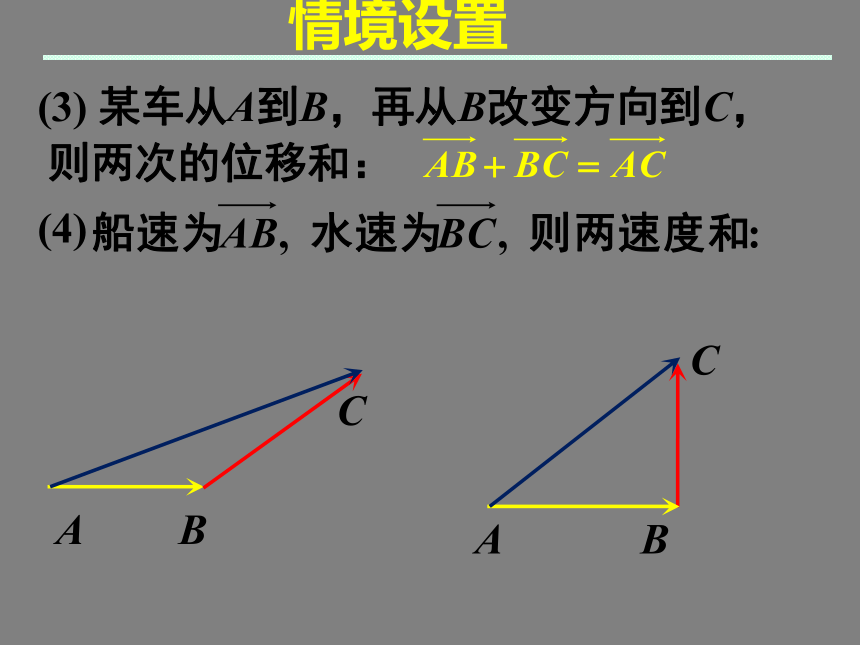
是长度为3的向量呢?复习引入情境设置(3) 某车从A到B,再从B改变方向到C,
则两次的位移和: A BC(4)A BC讲授新课 向量的加法: 求两个向量和的运算, 叫做向量的
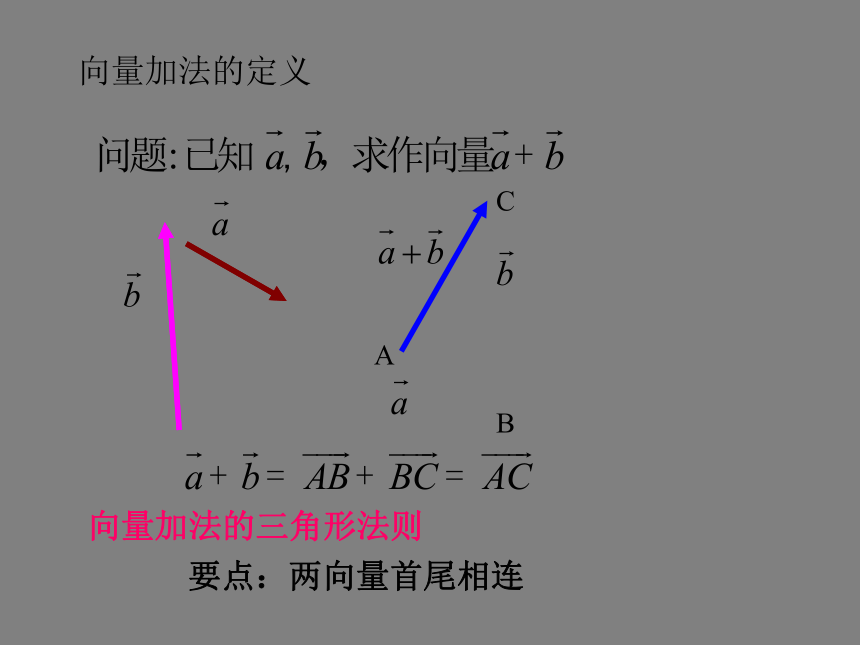
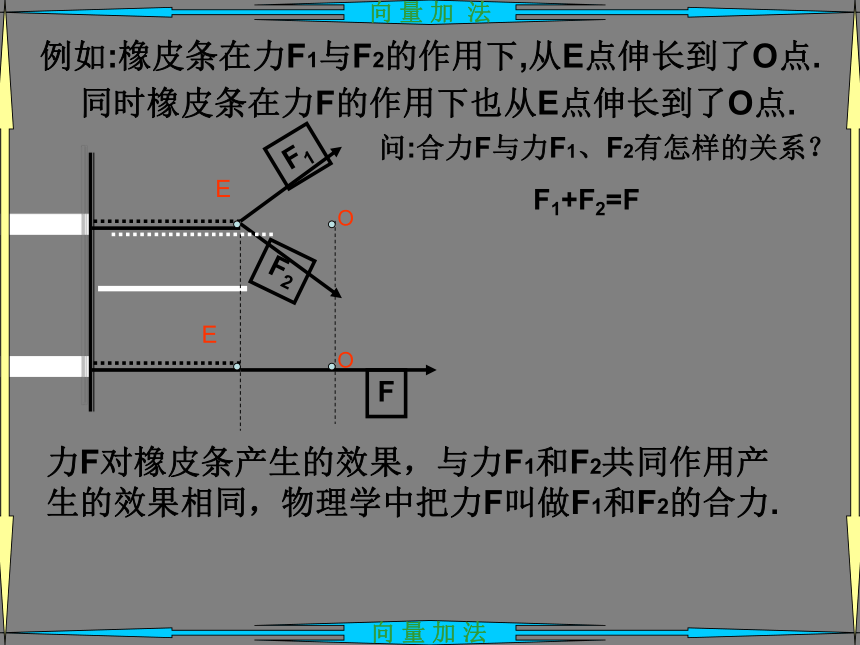
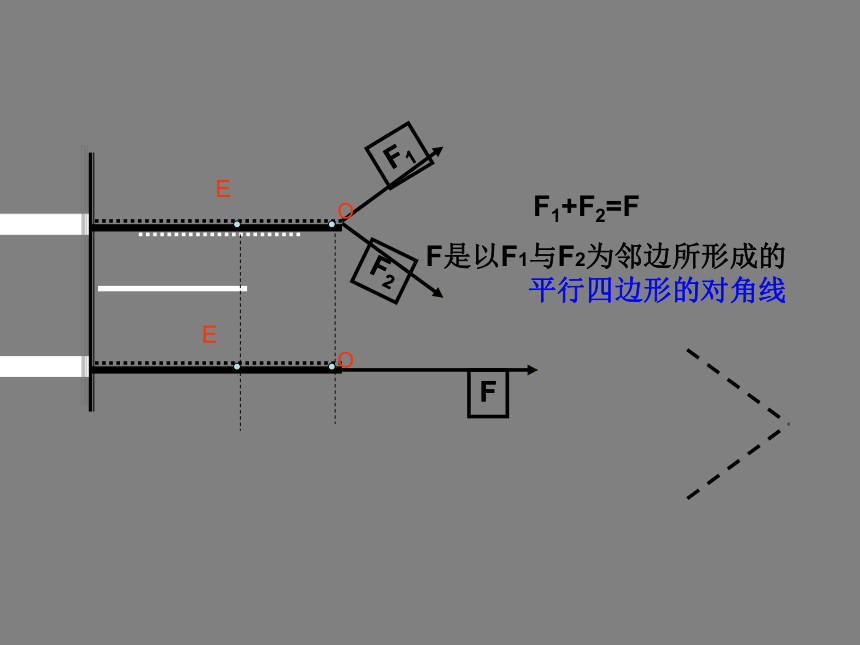
加法.A·CB向量加法的三角形法则要点:两向量首尾相连向量加法的定义向 量 加 法向 量 加 法 EOOE例如:橡皮条在力F1与F2的作用下,从E点伸长到了O点.同时橡皮条在力F的作用下也从E点伸长到了O点.问:合力F与力F1、F2有怎样的关系?F1+F2=F力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.EOOEF1+F2=FF是以F1与F2为邻边所形成的
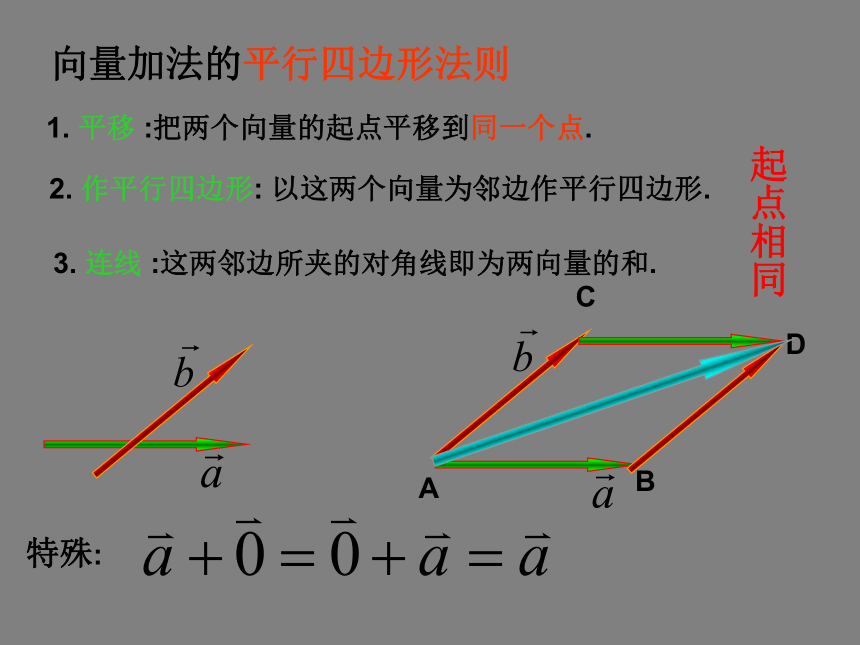
平行四边形的对角线向量加法的平行四边形法则1. 平移 :把两个向量的起点平移到同一个点.2. 作平行四边形: 以这两个向量为邻边作平行四边形.3. 连线 :这两邻边所夹的对角线即为两向量的和.起点相同探究:求和时用三角形法则与平行四边形法则
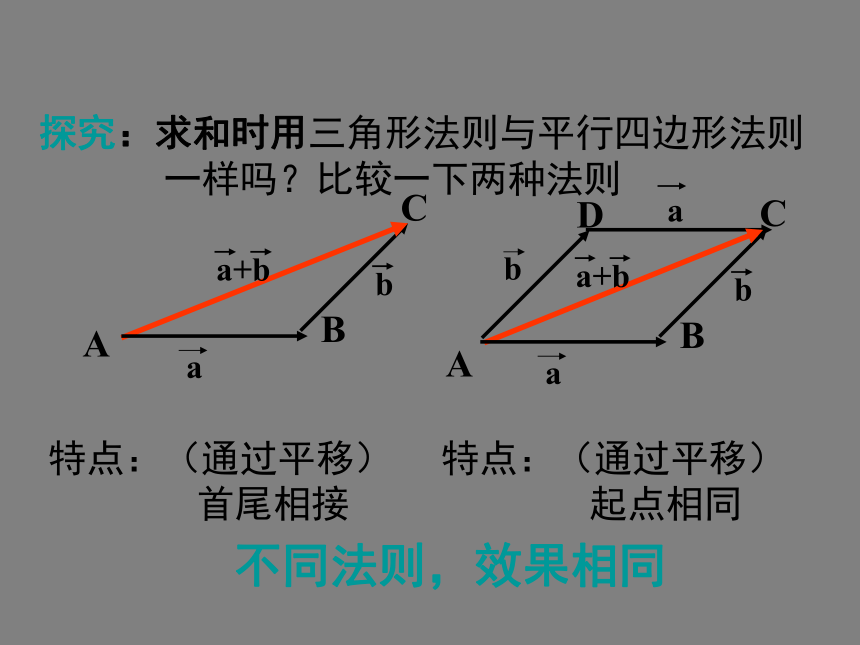
一样吗?比较一下两种法则特点:(通过平移)
首尾相接特点:(通过平移)
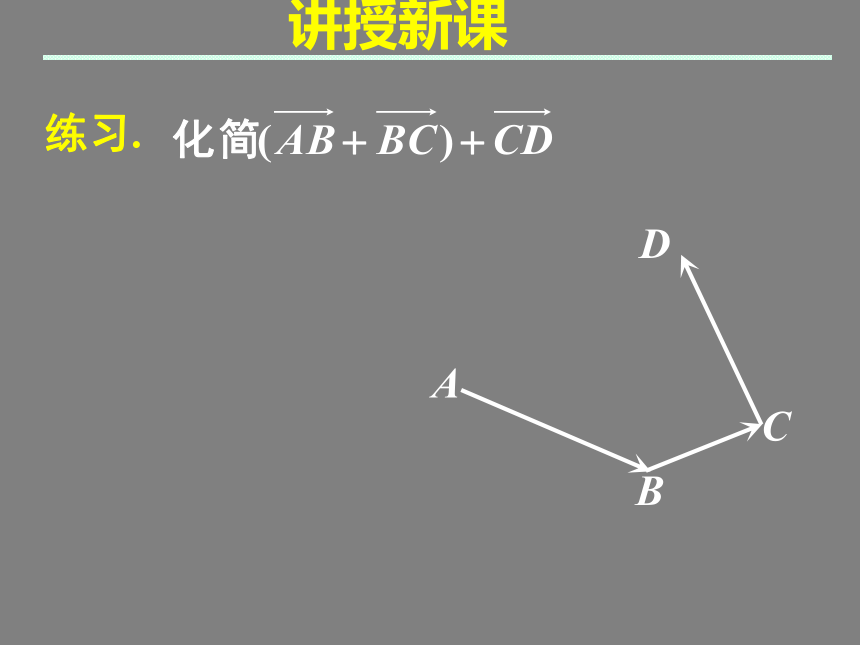
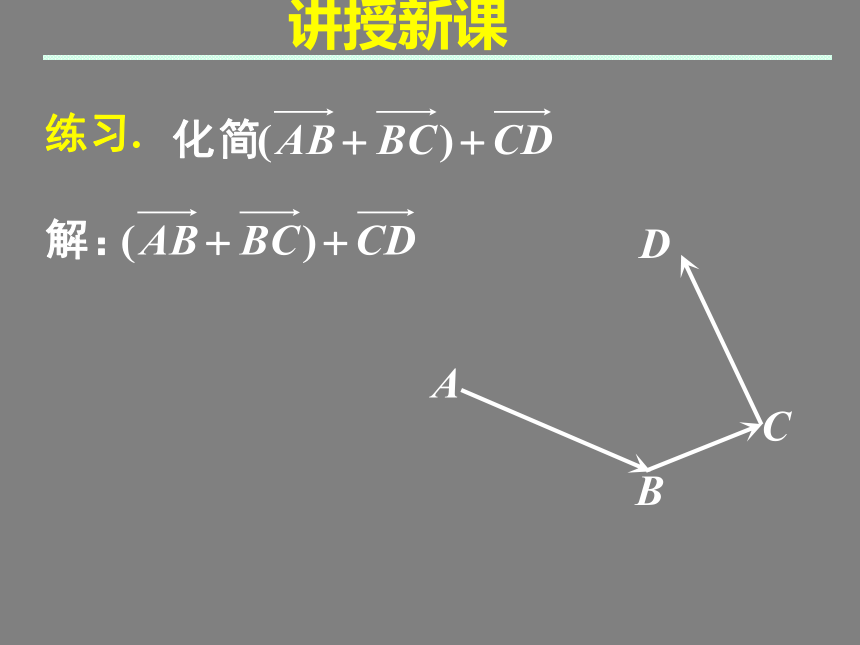
起点相同不同法则,效果相同ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.AB 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCE 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCE 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEF 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEF 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课D讲授新课探究:
(1)两向量的和与两个数的和有什么关系? 讲授新课探究:
(1)两向量的和与两个数的和有什么关系? 两向量的和仍是一个向量.讲授新课(2)探究:讲授新课(2)探究:讲授新课 (2)探究:情境设置ABC 某人从A到B,再从B按原方向到C,
则两次的位移和:讲授新课(2)探究:讲授新课 (2)探究:情境设置CAB(2) 若上题改为从A到B,再从B按反方向
到C, 则两次的位移和:讲授新课(2)探究:讲授新课 (2)探究:讲授新课 (2)探究:讲授新课讲授新课OA讲授新课OAB讲授新课OAB讲授新课OAB讲授新课3. 加法的交换律和平行四边形法则问题:OAB讲授新课3. 加法的交换律和平行四边形法则问题:OAB讲授新课(1)向量加法的平行四边形法则
(对于两个向量共线不适应)
(2)向量加法的交换律: 3. 加法的交换律和平行四边形法则BCD讲授新课4. 你能证明向量加法的结合律:讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:讲授新课例2. 长江两岸之间没有大桥的地方,常常通过
轮渡进行运输.如图所示,一艘船从长江南岸A
点出发,以5km/h的速度向垂直于对岸的方向
行驶,同时江水的速度为向东2km/h.
试用向量表示江水速度、船速以及船实际航
行的速度(保留两个有效数字) ;
(2)求船实际航行的速度的大小与方向(用江水
速度间的夹角表示, 精确到度).讲授新课例2. 长江两岸之间没有大桥的地方,常常通过
轮渡进行运输.如图所示,一艘船从长江南岸A
点出发,以5km/h的速度向垂直于对岸的方向
行驶,同时江水的速度为向东2km/h.
试用向量表示江水速度、船速以及船实际航
行的速度(保留两个有效数字) ;
(2)求船实际航行的速度的大小与方向(用江水
速度间的夹角表示, 精确到度).BACD讲授新课变式1.一艘船从A点出发以 km/h的速
度向垂直于对岸的方向行驶,船的实际航
行速度的大小为4km/h,求水流的速度.讲授新课变式2. 一艘船从A点出发以v1的速度向垂直
于对岸的方向行驶,同时河水的流速为v2,
船的实际航行的速度的大小为4km/h,方向
与水流间的夹角是60o,求v1和v2.讲授新课变式2. 一艘船从A点出发以v1的速度向垂直
于对岸的方向行驶,同时河水的流速为v2,
船的实际航行的速度的大小为4km/h,方向
与水流间的夹角是60o,求v1和v2.练习. 教材P.84第1、2题. 向量加法的几何意义;
交换律和结合律;
当且仅当方向相同时取等号.课堂小结 阅读教材P.80-P.84;
《习案》作业十八.课后作业 你能用向量加法证明:两条对
角线互相平分的四边形是平行四边
形吗?课后思考
及其几何意义
1、什么叫向量? 2、什么叫共线向量?既有大小又有方向的量叫向量
方向相同或相反的非零向量叫共线向量3、什么叫相等向量?长度相等且方向相同的向量叫相等向量。
也叫平行向量回顾旧知问题
数可进行加法运算:1+2=3 .那
么向量的加法是怎样定义的?长度是1
的向量与长度是2的向量相加是否一定
是长度为3的向量呢?复习引入情境设置(3) 某车从A到B,再从B改变方向到C,
则两次的位移和: A BC(4)A BC讲授新课 向量的加法: 求两个向量和的运算, 叫做向量的
加法.A·CB向量加法的三角形法则要点:两向量首尾相连向量加法的定义向 量 加 法向 量 加 法 EOOE例如:橡皮条在力F1与F2的作用下,从E点伸长到了O点.同时橡皮条在力F的作用下也从E点伸长到了O点.问:合力F与力F1、F2有怎样的关系?F1+F2=F力F对橡皮条产生的效果,与力F1和F2共同作用产生的效果相同,物理学中把力F叫做F1和F2的合力.EOOEF1+F2=FF是以F1与F2为邻边所形成的
平行四边形的对角线向量加法的平行四边形法则1. 平移 :把两个向量的起点平移到同一个点.2. 作平行四边形: 以这两个向量为邻边作平行四边形.3. 连线 :这两邻边所夹的对角线即为两向量的和.起点相同探究:求和时用三角形法则与平行四边形法则
一样吗?比较一下两种法则特点:(通过平移)
首尾相接特点:(通过平移)
起点相同不同法则,效果相同ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.ABCD讲授新课练习.AB 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课ABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABC 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCE 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCE 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEF 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEF 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课DABCEFKJ 如果三个向量相加,四个向量相加,
…n 个向量相加,和向量又如何?讲授新课D讲授新课探究:
(1)两向量的和与两个数的和有什么关系? 讲授新课探究:
(1)两向量的和与两个数的和有什么关系? 两向量的和仍是一个向量.讲授新课(2)探究:讲授新课(2)探究:讲授新课 (2)探究:情境设置ABC 某人从A到B,再从B按原方向到C,
则两次的位移和:讲授新课(2)探究:讲授新课 (2)探究:情境设置CAB(2) 若上题改为从A到B,再从B按反方向
到C, 则两次的位移和:讲授新课(2)探究:讲授新课 (2)探究:讲授新课 (2)探究:讲授新课讲授新课OA讲授新课OAB讲授新课OAB讲授新课OAB讲授新课3. 加法的交换律和平行四边形法则问题:OAB讲授新课3. 加法的交换律和平行四边形法则问题:OAB讲授新课(1)向量加法的平行四边形法则
(对于两个向量共线不适应)
(2)向量加法的交换律: 3. 加法的交换律和平行四边形法则BCD讲授新课4. 你能证明向量加法的结合律:讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:ADBC讲授新课4. 你能证明向量加法的结合律:讲授新课例2. 长江两岸之间没有大桥的地方,常常通过
轮渡进行运输.如图所示,一艘船从长江南岸A
点出发,以5km/h的速度向垂直于对岸的方向
行驶,同时江水的速度为向东2km/h.
试用向量表示江水速度、船速以及船实际航
行的速度(保留两个有效数字) ;
(2)求船实际航行的速度的大小与方向(用江水
速度间的夹角表示, 精确到度).讲授新课例2. 长江两岸之间没有大桥的地方,常常通过
轮渡进行运输.如图所示,一艘船从长江南岸A
点出发,以5km/h的速度向垂直于对岸的方向
行驶,同时江水的速度为向东2km/h.
试用向量表示江水速度、船速以及船实际航
行的速度(保留两个有效数字) ;
(2)求船实际航行的速度的大小与方向(用江水
速度间的夹角表示, 精确到度).BACD讲授新课变式1.一艘船从A点出发以 km/h的速
度向垂直于对岸的方向行驶,船的实际航
行速度的大小为4km/h,求水流的速度.讲授新课变式2. 一艘船从A点出发以v1的速度向垂直
于对岸的方向行驶,同时河水的流速为v2,
船的实际航行的速度的大小为4km/h,方向
与水流间的夹角是60o,求v1和v2.讲授新课变式2. 一艘船从A点出发以v1的速度向垂直
于对岸的方向行驶,同时河水的流速为v2,
船的实际航行的速度的大小为4km/h,方向
与水流间的夹角是60o,求v1和v2.练习. 教材P.84第1、2题. 向量加法的几何意义;
交换律和结合律;
当且仅当方向相同时取等号.课堂小结 阅读教材P.80-P.84;
《习案》作业十八.课后作业 你能用向量加法证明:两条对
角线互相平分的四边形是平行四边
形吗?课后思考
