人教A版数学必修四2.4 平面向量的数量积 课件 (共24张PPT)
文档属性
| 名称 | 人教A版数学必修四2.4 平面向量的数量积 课件 (共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-19 00:00:00 | ||
图片预览






文档简介
课件24张PPT。平面向量数量积教学目标重难点教学目标:
1.掌握平面向量的数量积及其几何意 义;
2.掌握平面向量数量积的重要性质及
运算律;
3.平面向量的数量积简单应用;
4.掌握向量垂直的条件.
教学重点:平面向量的数量积定义
教学难点:平面向量数量积的定义及
运算律的理解平面向量数量积的应用问题1.一个游泳爱好者想游到长江的正对岸(此段两岸平行),他以恒定的速度垂
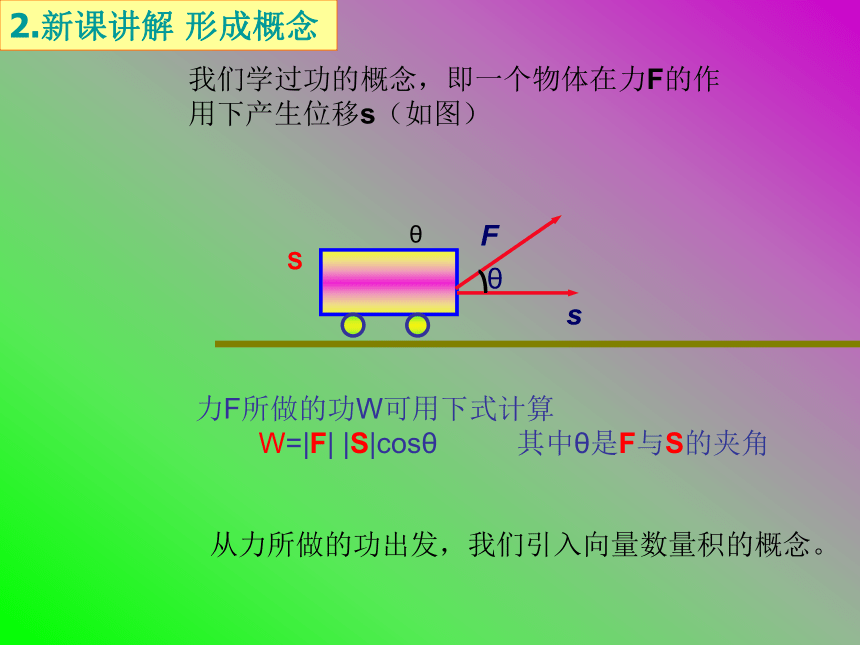
直于河岸方向行驶,能否到达目的地?问题2.在单杠上做引体向上运动,为节省体力,两臂夹角应越大还是越小?为解决这些问题,我们开始本节知识的学习。1.提出问题 引入新课我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θS力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
2.新课讲解 形成概念已知两个非零向量a与b,它们的夹角为θ,我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),记作a·b
a·b=|a| |b| cosθ
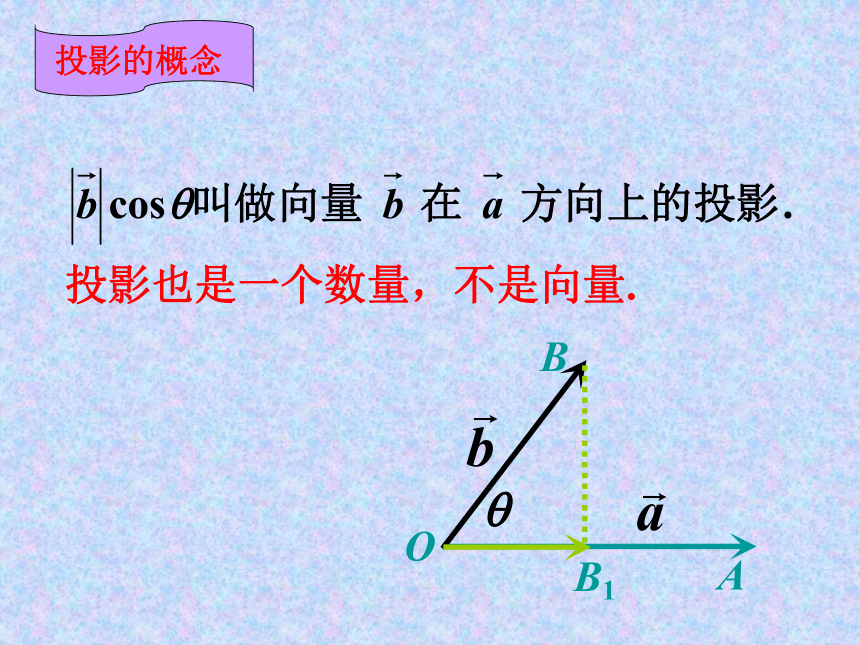
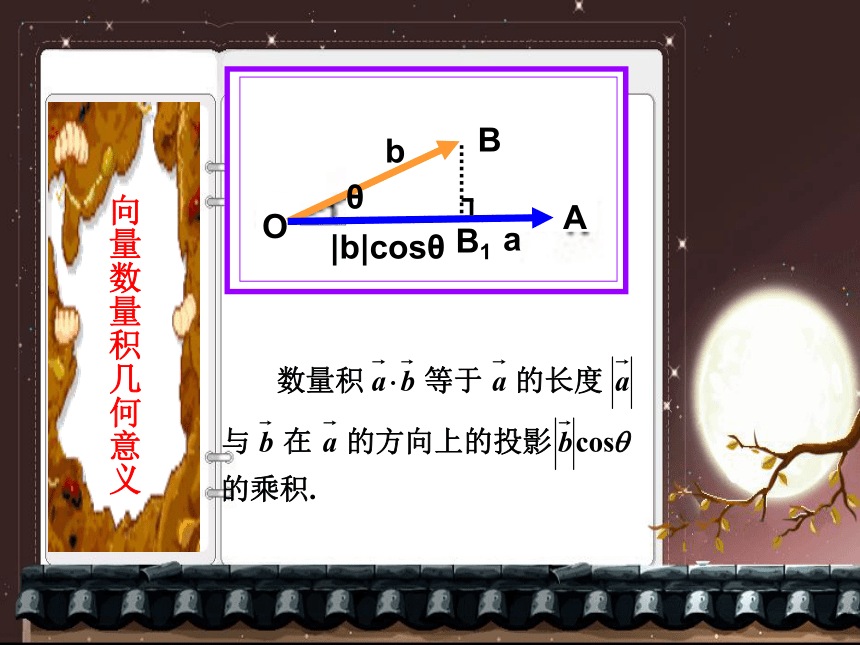
记法“a·b”中间的“ · ”不可以省略,也不可以用“”代替。注意:向量的数量积是一个数量。数量积定义思考:向量的数量积是一个数量,那么它什么时候为正,什么时候为负?当0°≤θ < 90°时a·b为正,a·b为正θ不一定为锐角正负零当90°<θ ≤180°时a·b为负。 a·b为负θ不一定为钝角当θ =90°时a·b为零。a·b=|a| |b| cosθ投影也是一个数量,不是向量.OBAB1投影的概念BOB1当?为直角时
投影为0;ABOB1ABO(B1)当?为锐角时
投影为正值; 当?为钝角时
投影为负值;A当? = 0?时投影为 当? = 180?时投影为向量数量积几何意义重要性质(点积为零是判定两向量垂直的条件)判断下列各题是否正确(1)若a=0,则对任意向量b,有a·b=0-----
(2)若a≠0,则对任意非零向量b,有a·b≠0--
(3)若a≠0,且a·b=0,则b=0 -------------------
(4)若a·b=0,则a=0或b=0 ---------------------
(5)对任意向量a有a2=│a│2 ----------------
(6)若a≠0且a·b=a·c,则b=c -------------------
(√)(× )( ×)(× )(√ )(× )课堂练习数量积的运算律:如图可知:3.性质讲解 深化概念求向量的数量积及向量的模 例1. 已知|a|=3,|b|=4且a与b的夹角为θ=120°,求:a·b,(a+b) 2,|a-b|.分析:根据向量的运算律求(a+b)2,|a-b|,求模时转化为求向量的平方问题,即|a|2=a2.点评: 利用|a|2=a2求向量的模时转化为求向量的平方问题.4.例题剖析 加强应用题型一题型二判断三角形形状例2 已知△ABC中,试判断△ABC的形状.题型三向量的垂直问题例3 已知|a|=3,|b|=4且a与b不共线.k为何值时,向量(a+kb)与(a-kb)互相垂直?分析:根据向量(a+kb)与(a-kb)互相垂直的条件列出关于k的关系式,求关于k的方程.题型四2.已知O为△ABC所在平面内一点,且满足
试判断△ABC的形状.3.已知|a|=2,|b|=1,a与b的夹角为 ,若向量2a+kb与a+b垂直,求k的值.随堂讨论(2011·重庆高考理科)已知单位向量的夹角为,则 【思路点拨】解答本题可利用结合向量的数量积运算来求解.【精讲精析】由题意知
答案:链接高考 (2011·全国高考理科· )设向量满足,则的最大值等于
A. 2B.C.D.1【思路点拨】本题按照题目要求构造出如右图所示的几何图形,然后
分析观察不难得到当线段AC为直径时,最大.【精讲精析】选A.如图,构造
所以A、B、C、D四点共圆,分析可知当线段AC为直径时,最大,最大值为2.1.由所学知识可知,受
水流速度的影响,他
将游到对岸的下方2.夹角越小越省力答课前问课堂小结 1、本节课学习的主要内容是什么?
2、平面向量数量积的两个基本应用是什么?
3、我们是按照怎样的思维模式进行概念的归纳 和性质的探究?在运算律的探究过程中,渗透了哪些数学思想?作业布置:课本P108习题2.4A组7、9、11
B组2 、 4谢谢大家
1.掌握平面向量的数量积及其几何意 义;
2.掌握平面向量数量积的重要性质及
运算律;
3.平面向量的数量积简单应用;
4.掌握向量垂直的条件.
教学重点:平面向量的数量积定义
教学难点:平面向量数量积的定义及
运算律的理解平面向量数量积的应用问题1.一个游泳爱好者想游到长江的正对岸(此段两岸平行),他以恒定的速度垂
直于河岸方向行驶,能否到达目的地?问题2.在单杠上做引体向上运动,为节省体力,两臂夹角应越大还是越小?为解决这些问题,我们开始本节知识的学习。1.提出问题 引入新课我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)θS力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
从力所做的功出发,我们引入向量数量积的概念。
2.新课讲解 形成概念已知两个非零向量a与b,它们的夹角为θ,我们把数量|a| |b|cosθ叫做a与b的数量积(或内积),记作a·b
a·b=|a| |b| cosθ
记法“a·b”中间的“ · ”不可以省略,也不可以用“”代替。注意:向量的数量积是一个数量。数量积定义思考:向量的数量积是一个数量,那么它什么时候为正,什么时候为负?当0°≤θ < 90°时a·b为正,a·b为正θ不一定为锐角正负零当90°<θ ≤180°时a·b为负。 a·b为负θ不一定为钝角当θ =90°时a·b为零。a·b=|a| |b| cosθ投影也是一个数量,不是向量.OBAB1投影的概念BOB1当?为直角时
投影为0;ABOB1ABO(B1)当?为锐角时
投影为正值; 当?为钝角时
投影为负值;A当? = 0?时投影为 当? = 180?时投影为向量数量积几何意义重要性质(点积为零是判定两向量垂直的条件)判断下列各题是否正确(1)若a=0,则对任意向量b,有a·b=0-----
(2)若a≠0,则对任意非零向量b,有a·b≠0--
(3)若a≠0,且a·b=0,则b=0 -------------------
(4)若a·b=0,则a=0或b=0 ---------------------
(5)对任意向量a有a2=│a│2 ----------------
(6)若a≠0且a·b=a·c,则b=c -------------------
(√)(× )( ×)(× )(√ )(× )课堂练习数量积的运算律:如图可知:3.性质讲解 深化概念求向量的数量积及向量的模 例1. 已知|a|=3,|b|=4且a与b的夹角为θ=120°,求:a·b,(a+b) 2,|a-b|.分析:根据向量的运算律求(a+b)2,|a-b|,求模时转化为求向量的平方问题,即|a|2=a2.点评: 利用|a|2=a2求向量的模时转化为求向量的平方问题.4.例题剖析 加强应用题型一题型二判断三角形形状例2 已知△ABC中,试判断△ABC的形状.题型三向量的垂直问题例3 已知|a|=3,|b|=4且a与b不共线.k为何值时,向量(a+kb)与(a-kb)互相垂直?分析:根据向量(a+kb)与(a-kb)互相垂直的条件列出关于k的关系式,求关于k的方程.题型四2.已知O为△ABC所在平面内一点,且满足
试判断△ABC的形状.3.已知|a|=2,|b|=1,a与b的夹角为 ,若向量2a+kb与a+b垂直,求k的值.随堂讨论(2011·重庆高考理科)已知单位向量的夹角为,则 【思路点拨】解答本题可利用结合向量的数量积运算来求解.【精讲精析】由题意知
答案:链接高考 (2011·全国高考理科· )设向量满足,则的最大值等于
A. 2B.C.D.1【思路点拨】本题按照题目要求构造出如右图所示的几何图形,然后
分析观察不难得到当线段AC为直径时,最大.【精讲精析】选A.如图,构造
所以A、B、C、D四点共圆,分析可知当线段AC为直径时,最大,最大值为2.1.由所学知识可知,受
水流速度的影响,他
将游到对岸的下方2.夹角越小越省力答课前问课堂小结 1、本节课学习的主要内容是什么?
2、平面向量数量积的两个基本应用是什么?
3、我们是按照怎样的思维模式进行概念的归纳 和性质的探究?在运算律的探究过程中,渗透了哪些数学思想?作业布置:课本P108习题2.4A组7、9、11
B组2 、 4谢谢大家
