正弦、余弦 课件
图片预览




文档简介
课件20张PPT。第一章
直角三角形的边角关系1.2 认识三角函数(二)
复习回顾1、我们怎样判断梯子的倾斜程度?2、正切是如何定义的? 用倾斜角的对边与邻边之比来刻画梯子的倾斜程度 在Rt△ABC 中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA =
本领大不大,
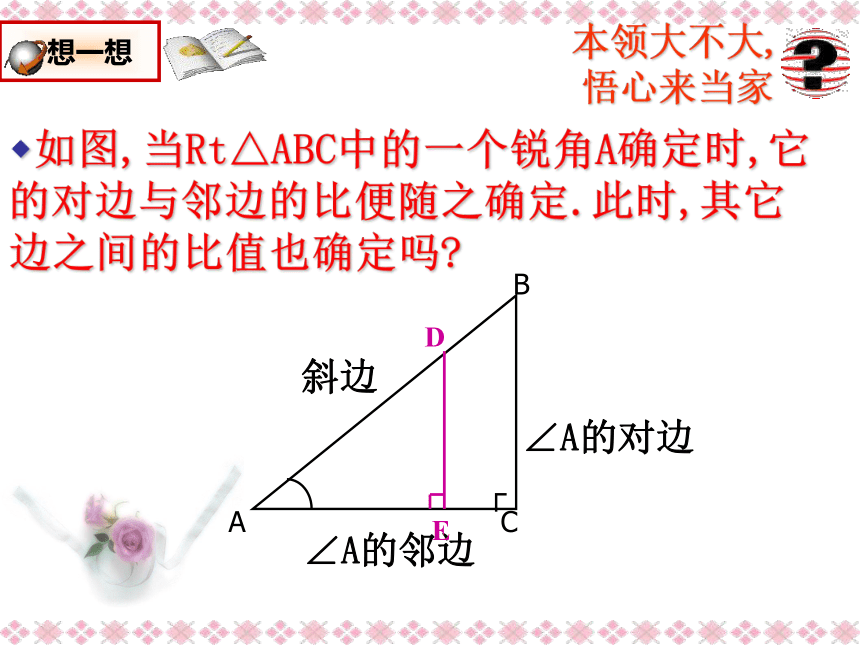
悟心来当家如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?ABC∠A的对边∠A的邻边┌斜边如图,当Rt△ABC中的一个锐角A确定时,
它的对边与邻边的比便随之确定.此时,
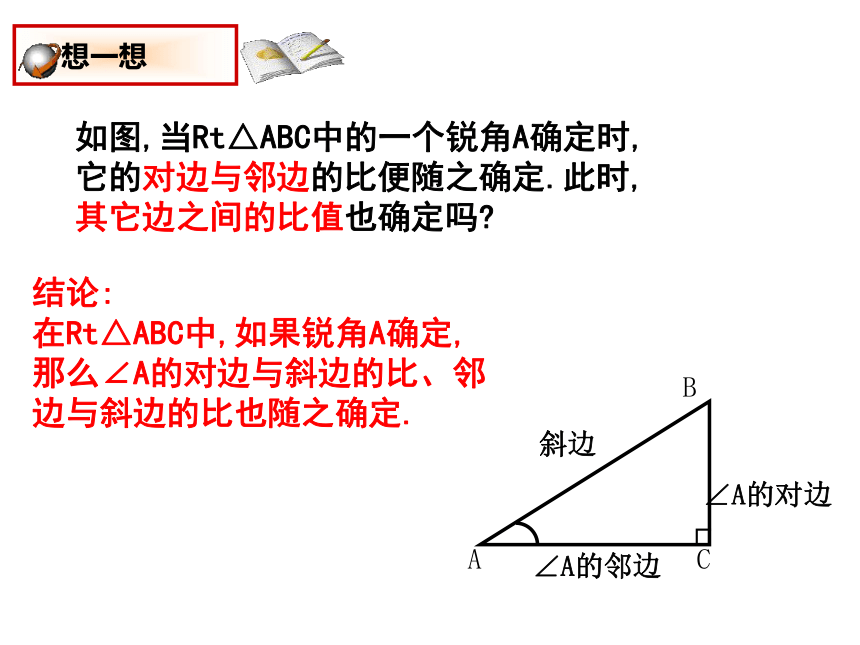
其它边之间的比值也确定吗?结论:
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.∠A的对边正弦与余弦在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦、余弦、正切都是∠A的三角函数.ABC∠A的对边∠A的邻边┌斜边
cosA=sinA= 注意:
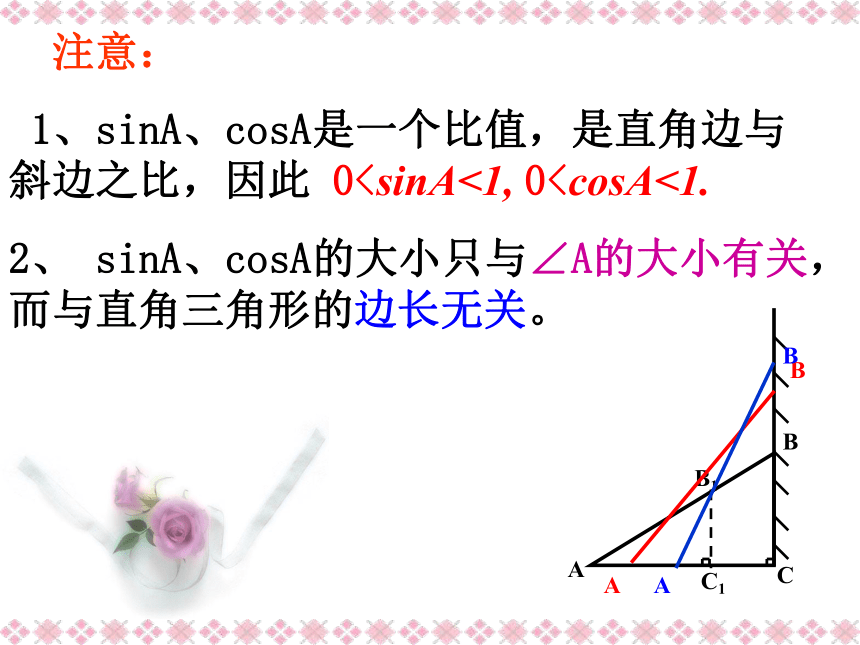
1、sinA、cosA是一个比值,是直角边与斜边之比,因此 02、 sinA、cosA的大小只与∠A的大小有关,而与直角三角形的边长无关。 课堂练习 如图,在Rt△ABC中, ∠C=90°,a、 b、c分别表示∠A、∠B、∠C的对边.1)若a=3,b=4,c=5,则sinA= , cosA= ,
tanA= , ∠B 呢?
2)如果已知c=5 和cosA=0.8,则b = .
3)如果已知b=4 和sinB=0.8,
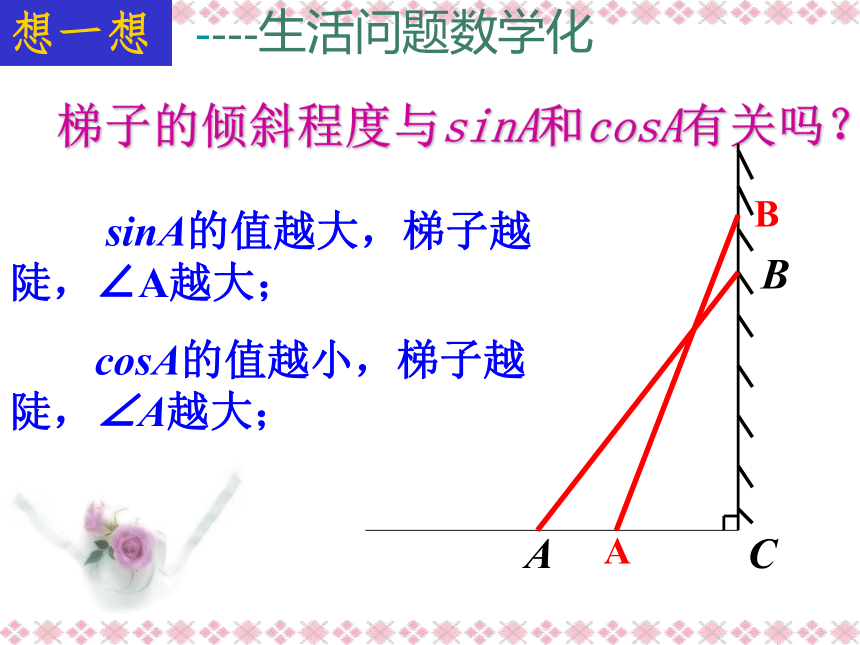
则c= .想一想 梯子的倾斜程度与sinA和cosA有关吗? sinA的值越大,梯子越陡,∠A越大;
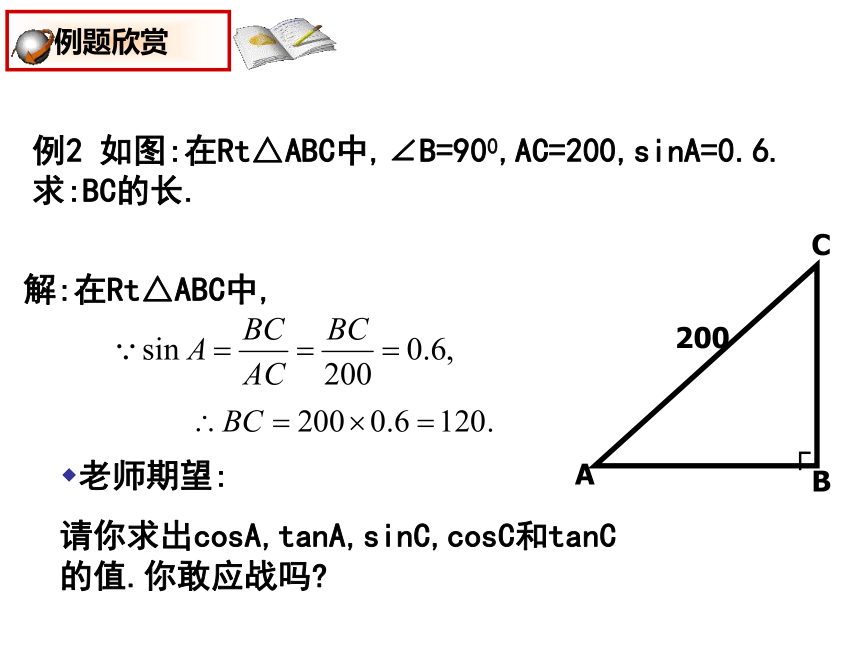
cosA的值越小,梯子越陡,∠A越大;ABCAB----生活问题数学化例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?200ACB┌解:在Rt△ABC中, 知识的内在联系求:AB,sinB.cosA=sinB (∠A+ ∠ B=900)1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.求:△ABC的周长.老师提示:过点A作AD垂直于BC于D.C3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.┌5.如图, ∠C=90°,CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.8.在Rt△ABC中,∠C=90°, AC=3,AB=6,
求sinA和cosB老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.9.在等腰△ABC中,AB=AC=13,BC=10,
求sinB,cosB.老师提示:
过点A作AD垂直于BC,垂足为D.
求锐角三角函数时,勾股定理的运用是很重要的.10.在梯形ABCD中AD//BC,AB=DC=13,AD=8,BC=18
求:sinB,cosB,tanB.老师提示:
梯形的高是梯形的常用辅助线,借助它可以转化为直角三角形.回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.回味无穷回顾,反思,深化1.锐角三角函数定义:请思考:在Rt△ABC中,
sinA和cosB有什么关系?
1. 如图,分别求∠α,∠β的正弦、余弦和正切.2.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD,sinC.3.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
求sin∠ACD,cos∠ACD和tan∠ACD.αβ9┐x4.在Rt△ABC中,∠C=90°,sinA和cosB有什么关系?知识的升华结束寄语 数学中的某些定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏极深.
——高斯再见
复习回顾1、我们怎样判断梯子的倾斜程度?2、正切是如何定义的? 用倾斜角的对边与邻边之比来刻画梯子的倾斜程度 在Rt△ABC 中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
tanA =
本领大不大,
悟心来当家如图,当Rt△ABC中的一个锐角A确定时,它的对边与邻边的比便随之确定.此时,其它边之间的比值也确定吗?ABC∠A的对边∠A的邻边┌斜边如图,当Rt△ABC中的一个锐角A确定时,
它的对边与邻边的比便随之确定.此时,
其它边之间的比值也确定吗?结论:
在Rt△ABC中,如果锐角A确定,那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.∠A的对边正弦与余弦在Rt△ABC中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即在Rt△ABC中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即锐角A的正弦、余弦、正切都是∠A的三角函数.ABC∠A的对边∠A的邻边┌斜边
cosA=sinA= 注意:
1、sinA、cosA是一个比值,是直角边与斜边之比,因此 0
tanA= , ∠B 呢?
2)如果已知c=5 和cosA=0.8,则b = .
3)如果已知b=4 和sinB=0.8,
则c= .想一想 梯子的倾斜程度与sinA和cosA有关吗? sinA的值越大,梯子越陡,∠A越大;
cosA的值越小,梯子越陡,∠A越大;ABCAB----生活问题数学化例2 如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.
求:BC的长.老师期望:
请你求出cosA,tanA,sinC,cosC和tanC的值.你敢应战吗?200ACB┌解:在Rt△ABC中, 知识的内在联系求:AB,sinB.cosA=sinB (∠A+ ∠ B=900)1.如图:在等腰△ABC中,AB=AC=5,BC=6.
求: sinB,cosB,tanB.求:△ABC的周长.老师提示:过点A作AD垂直于BC于D.C3.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B.缩小100倍
C.不变 D.不能确定4.已知∠A,∠B为锐角
(1)若∠A=∠B,则sinA sinB;
(2)若sinA=sinB,则∠A ∠B.┌5.如图, ∠C=90°,CD⊥AB.6.在上图中,若BD=6,CD=12.求cosA的值.7.如图,分别根据图(1)和图(2)求∠A的三个三角函数值.8.在Rt△ABC中,∠C=90°, AC=3,AB=6,
求sinA和cosB老师提示:
求锐角三角函数时,勾股定理的运用是很重要的.9.在等腰△ABC中,AB=AC=13,BC=10,
求sinB,cosB.老师提示:
过点A作AD垂直于BC,垂足为D.
求锐角三角函数时,勾股定理的运用是很重要的.10.在梯形ABCD中AD//BC,AB=DC=13,AD=8,BC=18
求:sinB,cosB,tanB.老师提示:
梯形的高是梯形的常用辅助线,借助它可以转化为直角三角形.回味无穷定义中应该注意的几个问题:1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.回味无穷回顾,反思,深化1.锐角三角函数定义:请思考:在Rt△ABC中,
sinA和cosB有什么关系?
1. 如图,分别求∠α,∠β的正弦、余弦和正切.2.在△ABC中,AB=5,BC=13,AD是BC边上的高,AD=4.求:CD,sinC.3.在Rt△ABC中,∠BCA=90°,CD是中线,BC=8,CD=5.
求sin∠ACD,cos∠ACD和tan∠ACD.αβ9┐x4.在Rt△ABC中,∠C=90°,sinA和cosB有什么关系?知识的升华结束寄语 数学中的某些定理具有这样的特性:它们极易从事实中归纳出来,但证明却隐藏极深.
——高斯再见
