用正多边形铺设地面 课件
图片预览



文档简介
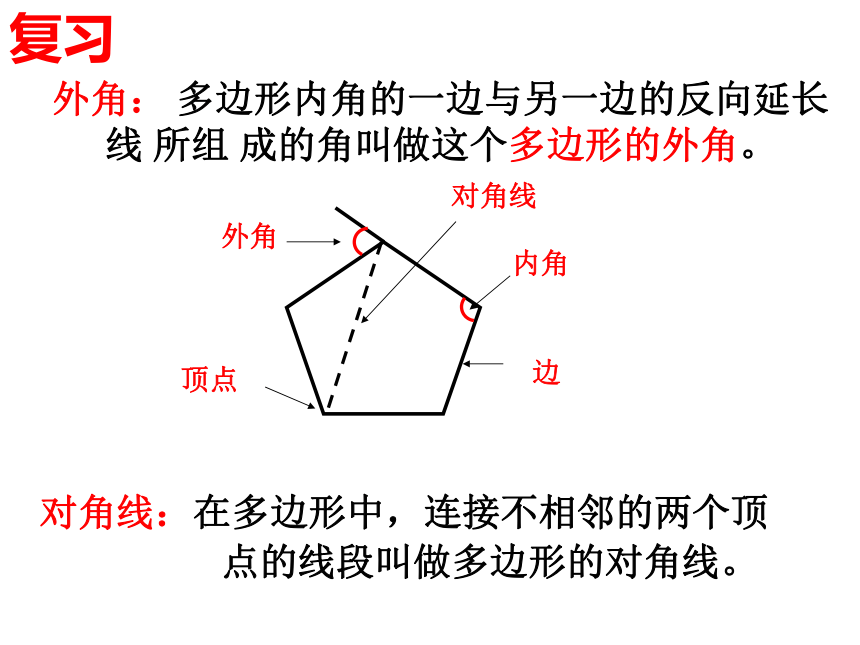
课件36张PPT。顶点内角边外角对角线对角线:在多边形中,连接不相邻的两个顶
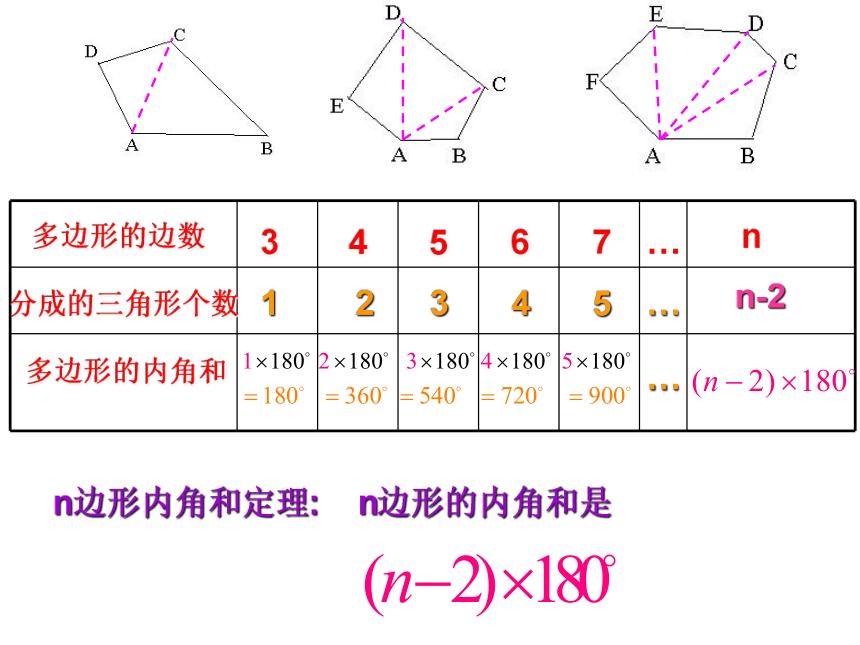
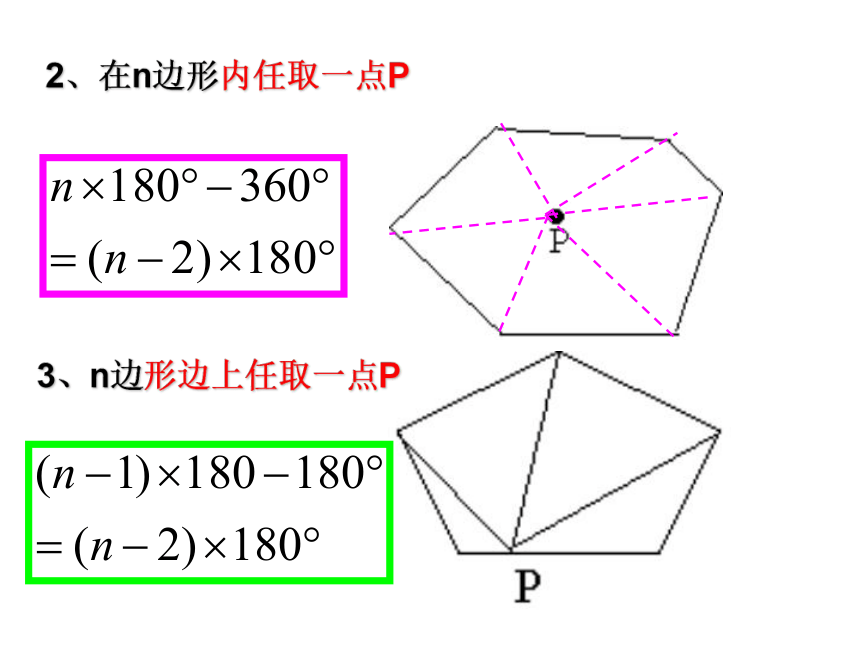
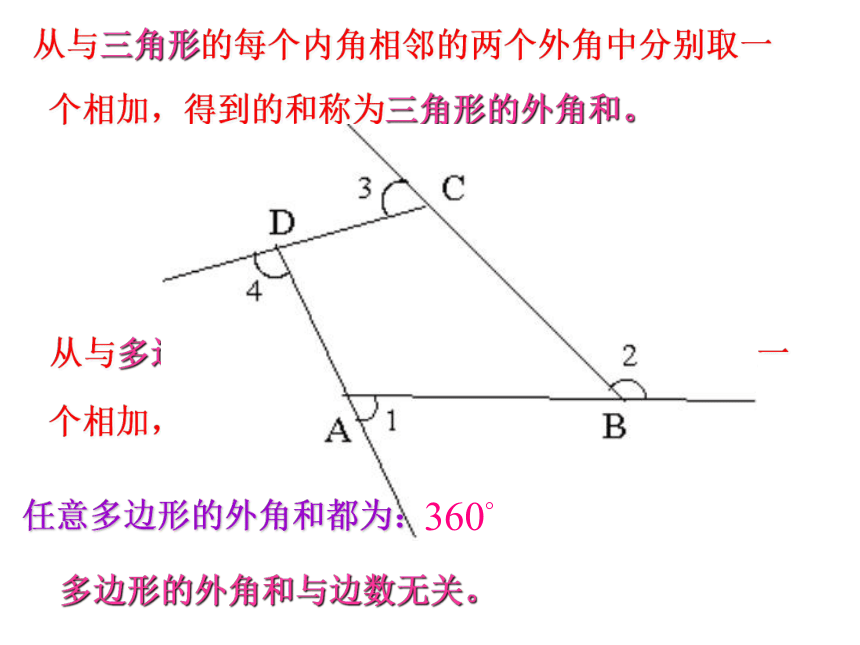
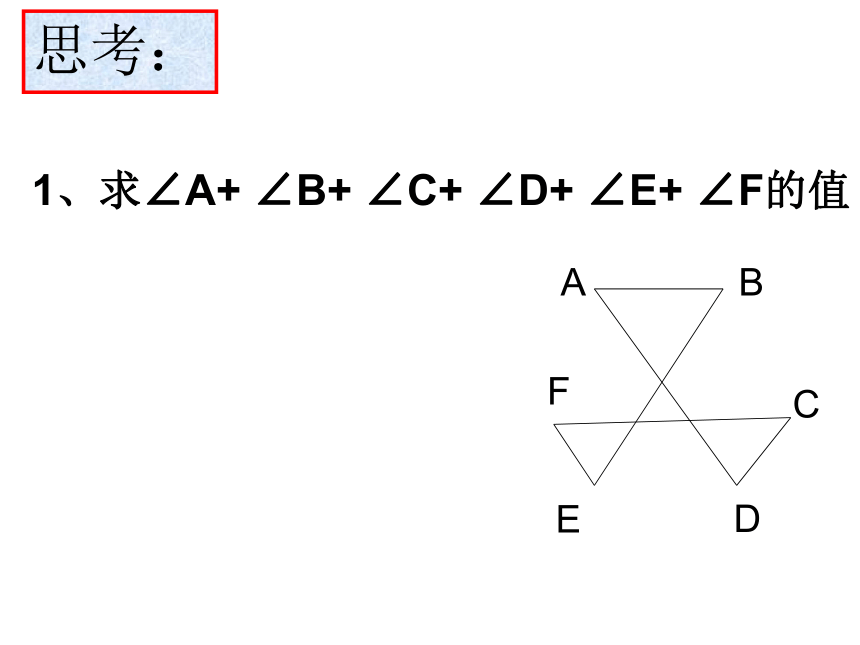
点的线段叫做多边形的对角线。外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。复习请问:四边形从一个顶点出发,能引出几条对角线?请问:五边形从一个顶点出发,能引出几条对角线?请问:六边形从一个顶点出发,能引出几条对角线?请问:N边形从一个顶点出发,能引出几条对角线? ……123N-3多边形的边数分成的三角形个数多边形的内角和3456…n1234…n-275…n边形内角和定理: n边形的内角和是 2、在n边形内任取一点P3、n边形边上任取一点P从与三角形的每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。任意多边形的外角和都为:多边形的外角和与边数无关。思考:1、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:2、求∠A+ ∠B+ ∠C+ ∠D
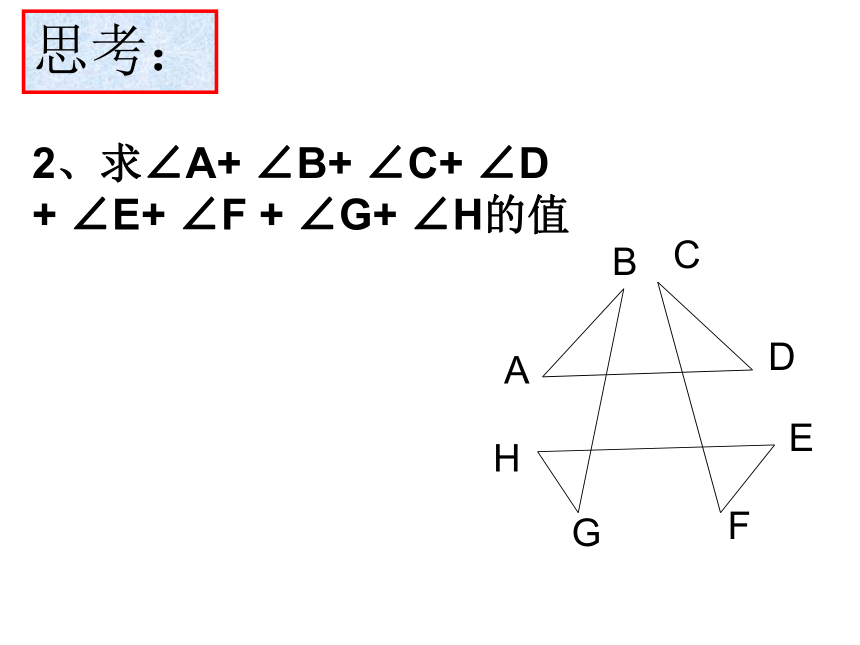
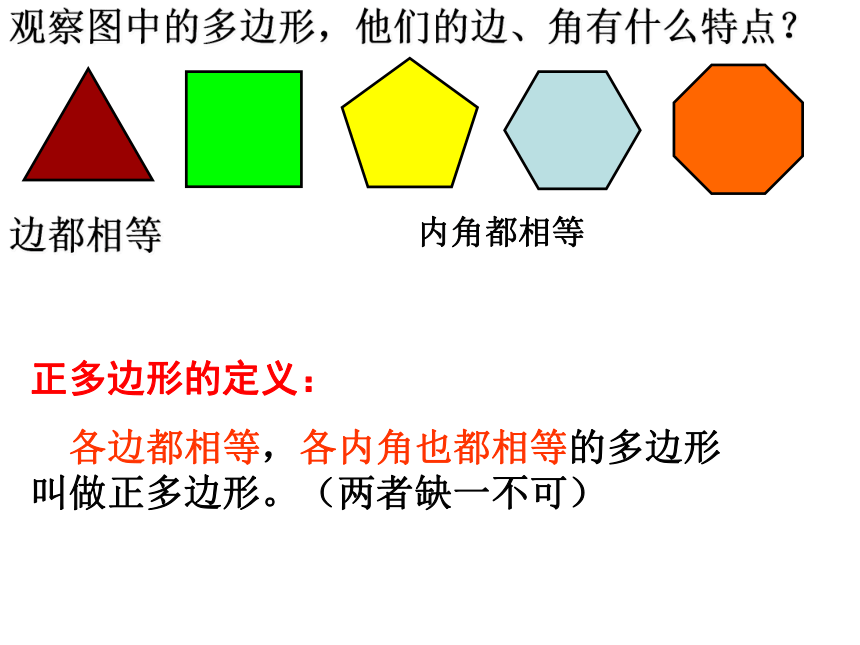
+ ∠E+ ∠F + ∠G+ ∠H的值9.3用正多边形铺设地面观察图中的多边形,他们的边、角有什么特点?内角都相等边都相等正多边形的定义:
各边都相等,各内角也都相等的多边形叫做正多边形。(两者缺一不可)
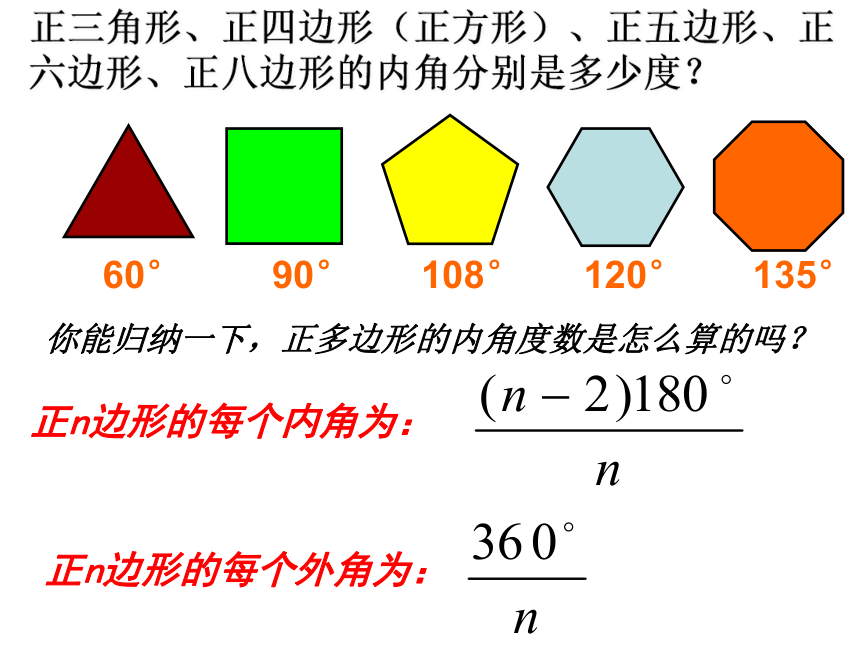
正n边形的每个内角为: 你能归纳一下,正多边形的内角度数是怎么算的吗?正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?60°90°108°120°135°正n边形的每个外角为: 用相同的正多边形
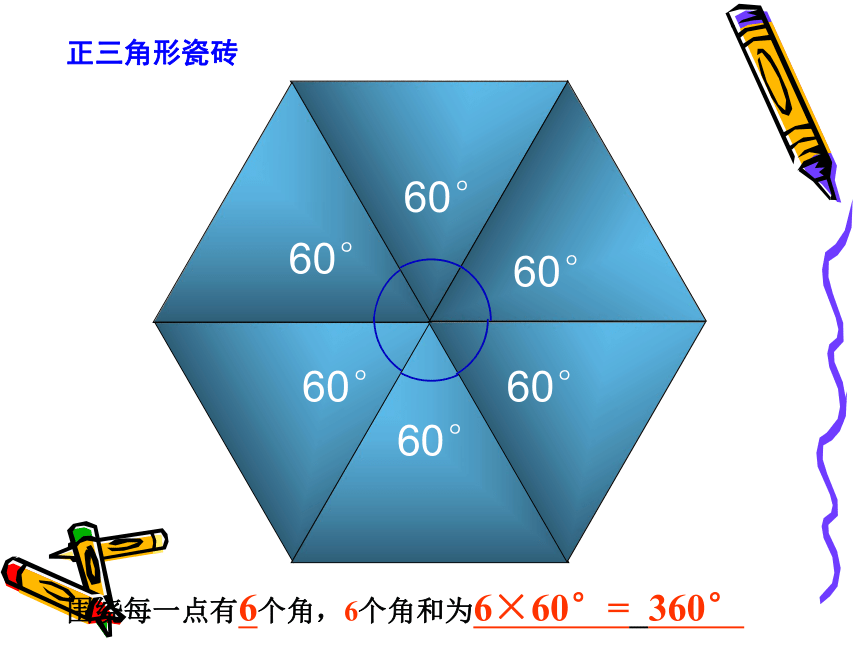
如何密铺?60°60°60°60°60°60°正三角形瓷砖围绕每一点有6个角,6个角和为6×60°= 360°90°90°90°90°正方形瓷砖围绕每一点有4个角,4个角和为4×90°=360°108°108°108°正五边形瓷砖围绕每一点有3个角,3个角和为3×108°= 324°≠360°120°120°120°正六边形瓷砖围绕每一点有3个角,3个角和为3×120°=360°正七边形正八边形呢?想一想,为什么?不能!也不能!>360°>360°正八边形的每个内角为 (8-2) ×180°÷8=135°围绕每一点有3个角,3个角和为3×135°=405°正七边形的每个内角为 (7-2) ×180°÷7≈128.6°围绕每一点有3个角,3个角和为3×128.6°=385.8°规律:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用相同的任意三角形、
任意四边形 能密铺吗?剪出一些形状、大小都一样的四边形,拼拼看,能否铺满地面。思考“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙。结论:形状、大小相同的任意四边形能镶嵌成平面图形把一些形状,大小相同的三角形能否镶嵌成平面图形?结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。想一想 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用两种正多边形
能密铺吗?如图:把相邻两行正三角形分开,添一行正方形,得到下面的图。它表明把正三角形和正方形结合在一起也能铺满地面。为什么?练习解: 3×60°+2 ×90°=360°
答:能铺满地面。分析:因为正三角形的内角为60度,正方形的内角为90度,这样用3块正三角形和2块正方形,他们的内角和为一个周角360度,所以能铺满地面。为什么以下几组图形能够如此巧妙的结合在一起?1.正八边形和正方形组合。1.正八边形和正方形组合。2.正十二边形和正三角形组合。 正十二边形和正三角形组合。 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用三种正多边形
能密铺吗?正十二边形、正六边形和正方形的组合。 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。练习题: 选择题: CCA小结1、能密铺的条件是什么?当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。2、能用同一种正多边形拼地板的正多边形有哪些?能用同一种正多边形拼地板的正多边形只有正三角形、正方形、正六边形.3.用相同的任意三角形、任意四边形 能密铺吗?结论1:形状、大小相同的任意四边形能镶嵌成平面图形
结论2:形状、大小相同的任意三角形能镶嵌成平面图形。用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由。解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即 m+ 2n= 6
满足题意的正整数解为
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形小结:或满足:
内角度数×m + 另一种内角度数×n+第三种内角度数×k =360°
的方程正整数解 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
点的线段叫做多边形的对角线。外角: 多边形内角的一边与另一边的反向延长 线 所组 成的角叫做这个多边形的外角。复习请问:四边形从一个顶点出发,能引出几条对角线?请问:五边形从一个顶点出发,能引出几条对角线?请问:六边形从一个顶点出发,能引出几条对角线?请问:N边形从一个顶点出发,能引出几条对角线? ……123N-3多边形的边数分成的三角形个数多边形的内角和3456…n1234…n-275…n边形内角和定理: n边形的内角和是 2、在n边形内任取一点P3、n边形边上任取一点P从与三角形的每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和。从与多边形的每个内角相邻的两个外角中分别取一个相加,得到的和称为多边形的外角和。任意多边形的外角和都为:多边形的外角和与边数无关。思考:1、求∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的值思考:2、求∠A+ ∠B+ ∠C+ ∠D
+ ∠E+ ∠F + ∠G+ ∠H的值9.3用正多边形铺设地面观察图中的多边形,他们的边、角有什么特点?内角都相等边都相等正多边形的定义:
各边都相等,各内角也都相等的多边形叫做正多边形。(两者缺一不可)
正n边形的每个内角为: 你能归纳一下,正多边形的内角度数是怎么算的吗?正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?60°90°108°120°135°正n边形的每个外角为: 用相同的正多边形
如何密铺?60°60°60°60°60°60°正三角形瓷砖围绕每一点有6个角,6个角和为6×60°= 360°90°90°90°90°正方形瓷砖围绕每一点有4个角,4个角和为4×90°=360°108°108°108°正五边形瓷砖围绕每一点有3个角,3个角和为3×108°= 324°≠360°120°120°120°正六边形瓷砖围绕每一点有3个角,3个角和为3×120°=360°正七边形正八边形呢?想一想,为什么?不能!也不能!>360°>360°正八边形的每个内角为 (8-2) ×180°÷8=135°围绕每一点有3个角,3个角和为3×135°=405°正七边形的每个内角为 (7-2) ×180°÷7≈128.6°围绕每一点有3个角,3个角和为3×128.6°=385.8°规律:
使用给定的某种正多边形,当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用相同的任意三角形、
任意四边形 能密铺吗?剪出一些形状、大小都一样的四边形,拼拼看,能否铺满地面。思考“任意四边形(指凸四边形)内角之和都等于360°。”因此,不管切下的四边形怎样歪七扭八,只要形状完全相同,4块相拼就能凑成360°,而且总能找到等长的边相接,使砖与砖之间不留缝隙。结论:形状、大小相同的任意四边形能镶嵌成平面图形把一些形状,大小相同的三角形能否镶嵌成平面图形?结论:形状、大小完全相同的任意三角形能镶嵌成平面图形。想一想 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用两种正多边形
能密铺吗?如图:把相邻两行正三角形分开,添一行正方形,得到下面的图。它表明把正三角形和正方形结合在一起也能铺满地面。为什么?练习解: 3×60°+2 ×90°=360°
答:能铺满地面。分析:因为正三角形的内角为60度,正方形的内角为90度,这样用3块正三角形和2块正方形,他们的内角和为一个周角360度,所以能铺满地面。为什么以下几组图形能够如此巧妙的结合在一起?1.正八边形和正方形组合。1.正八边形和正方形组合。2.正十二边形和正三角形组合。 正十二边形和正三角形组合。 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。用三种正多边形
能密铺吗?正十二边形、正六边形和正方形的组合。 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。练习题: 选择题: CCA小结1、能密铺的条件是什么?当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。2、能用同一种正多边形拼地板的正多边形有哪些?能用同一种正多边形拼地板的正多边形只有正三角形、正方形、正六边形.3.用相同的任意三角形、任意四边形 能密铺吗?结论1:形状、大小相同的任意四边形能镶嵌成平面图形
结论2:形状、大小相同的任意三角形能镶嵌成平面图形。用正三角形和正六边形材料铺地面,在一个顶点周围有几个正三角形和几个正六边形?说明你的理由。解:设在一个顶点周围有m个正三角形的角,n个正六边形的角。
由题意得 m×60°+ n×120°= 360°
即 m+ 2n= 6
满足题意的正整数解为
答:在一个顶点周围有4个正三角形和1个正六边形
或者在一个顶点周围有2个正三角形和2个正六边形小结:或满足:
内角度数×m + 另一种内角度数×n+第三种内角度数×k =360°
的方程正整数解 规律:
当围绕一点拼在一起的几个内角加在一起恰好组成一个周角( 360°)时,就能铺满地面。
