12.2全等三角形的判定(总复习)课件
文档属性
| 名称 | 12.2全等三角形的判定(总复习)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 364.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-22 13:45:02 | ||
图片预览


文档简介
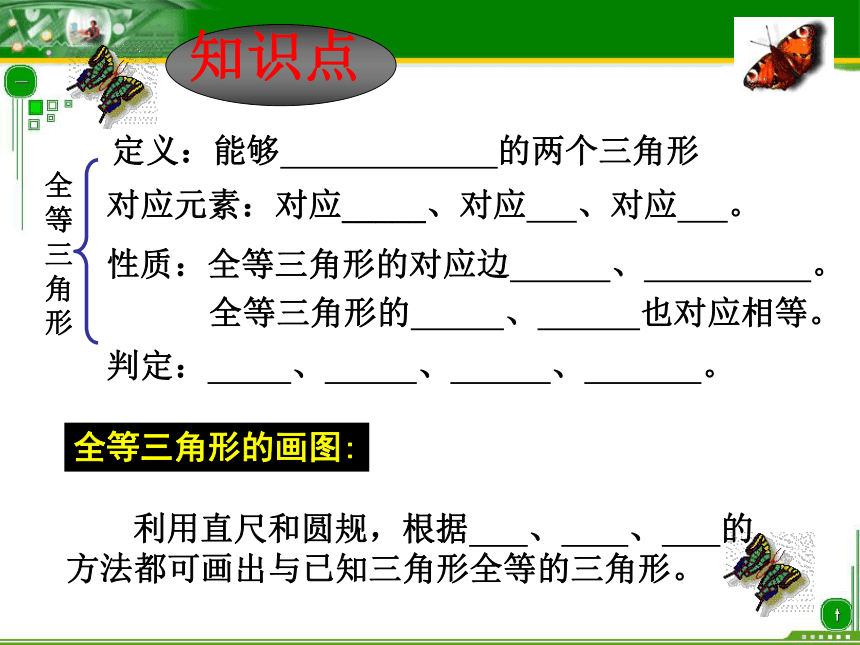
课件26张PPT。1第4讲 全等三角形的判定 全等三角形定义:能够 的两个三角形对应元素:对应_____、对应 、对应 。性质:全等三角形的对应边 、 。
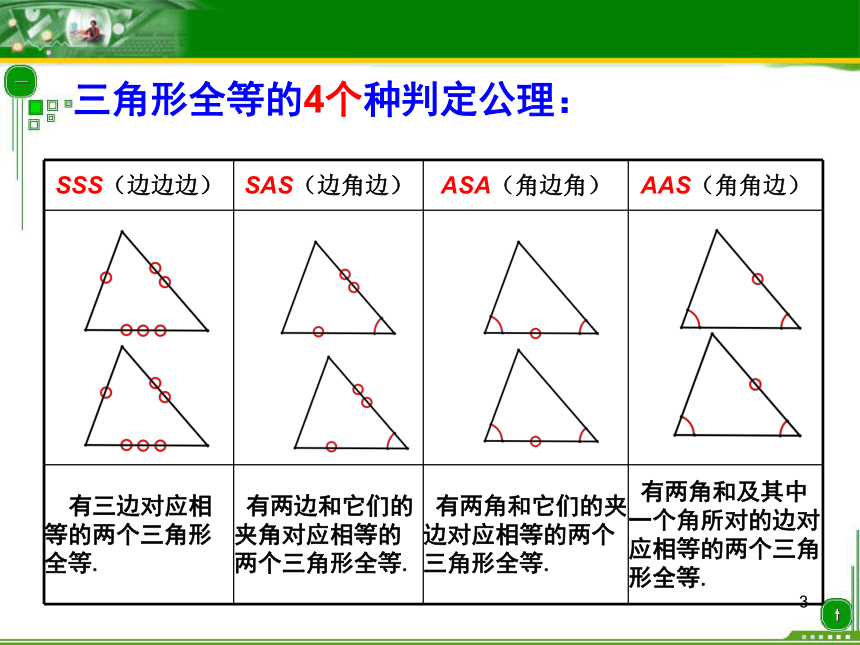
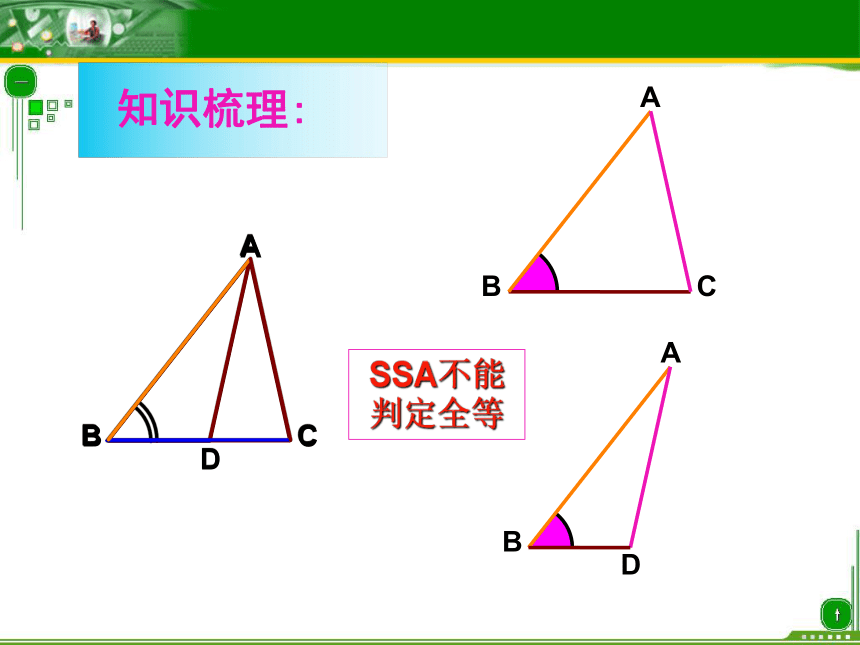
全等三角形的 、 也对应相等。判定: 、 、 、 。全等三角形的画图: 利用直尺和圆规,根据 、 、 的方法都可画出与已知三角形全等的三角形。 1三角形全等的4个种判定公理: ABDABCSSA不能判定全等谈谈本节课你有什么收获?你会证明三角形全等了吗?
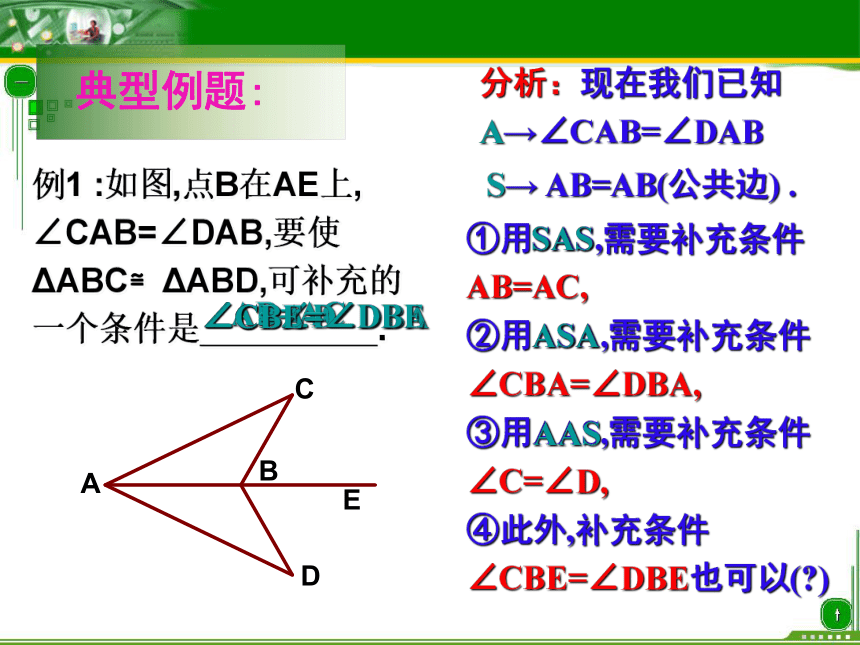
例1 :如图,点B在AE上,
∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
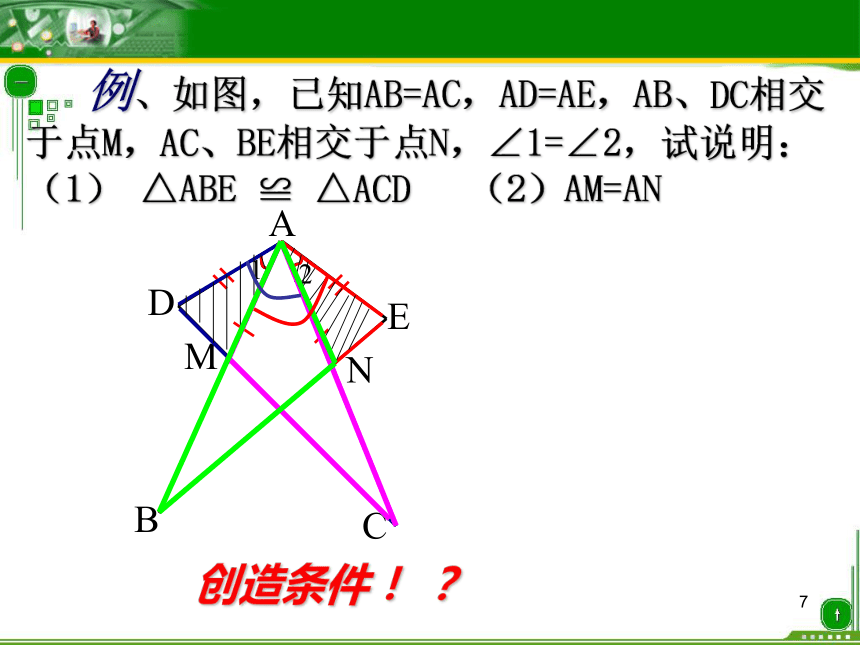
一个条件是 .分析:现在我们已知 A→∠CAB=∠DAB①用SAS,需要补充条件AB=AC, ②用ASA,需要补充条件∠CBA=∠DBA, ③用AAS,需要补充条件∠C=∠D, ④此外,补充条件∠CBE=∠DBE也可以(?) SASASAAASS→ AB=AB(公共边) .AB=AC ∠CBA=∠DBA∠C=∠D∠CBE=∠DBE1 例、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,试说明:(1) △ABE ≌ △ACD (2)AM=AN
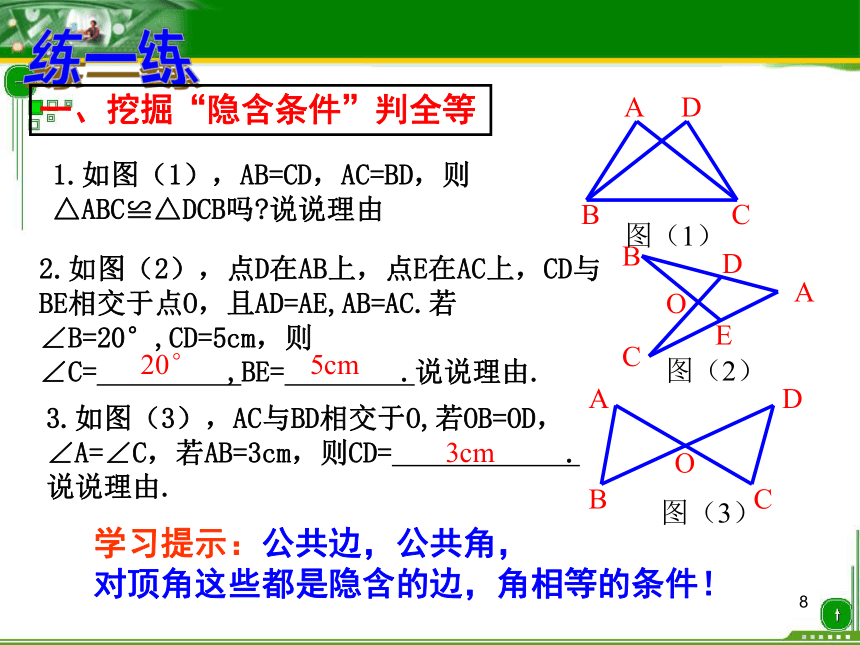
创造条件! ?1练一练一、挖掘“隐含条件”判全等20°5cm3cm学习提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!1
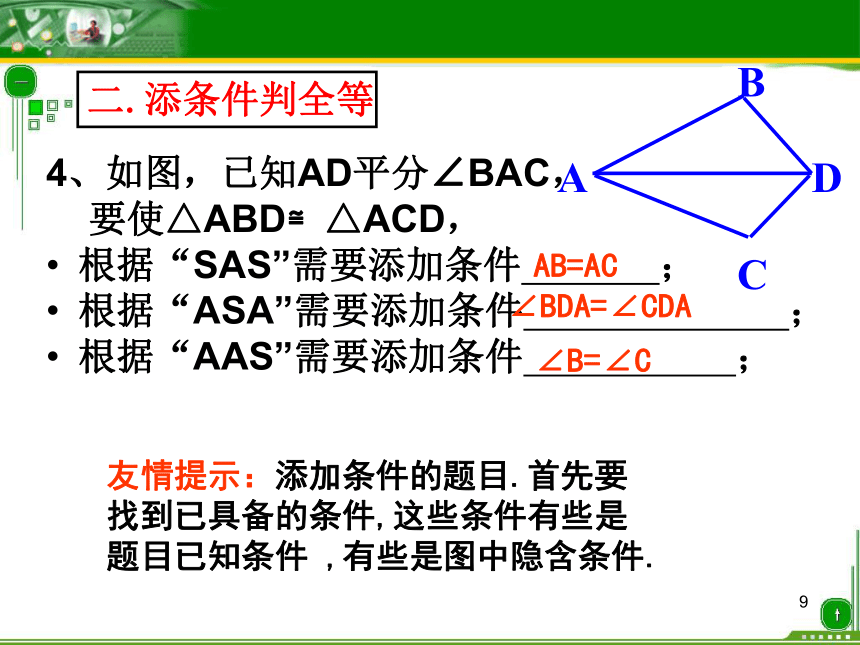
4、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;AB=AC∠BDA=∠CDA∠B=∠C友情提示:添加条件的题目.首先要
找到已具备的条件,这些条件有些是
题目已知条件 ,有些是图中隐含条件.二.添条件判全等1试一试 三、熟练转化“间接条件”判全等解答解答解答1 6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知)ADBCFE∴AE-FE=CF-EF(等量减等量,差相等)即AF=CE在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)1解:∵ ∠CAE=∠BAD(已知)∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量加等量,和相等)即∠BAC=∠DAE在△ABC和△ADE中, ∴△ABC≌ △ADE(AAS)例6 :如图,已知,AB=CD,
CE=DF,AE=BF,
则AE∥DF吗?为什么?证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD. ∴ ΔACE≌ΔBDF(SSS)在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知) ∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)1
实际运用
9. 测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。
15ABODC 如图是用两根长度相等的拉线固定电线杆的示意图.其中一根拉到B,另一根拉到C。那么C、B两端点到D的距离DC和DB的大小有何关系?说明理由。练一练 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DEECBAD如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。例8 :如图在 ΔABC中,
AD⊥BC于D,BE⊥AC
于E,AD交BE于F,
若BF=AC,那么∠ABC
的大小是( )A.40° B.50° C.60° D.45°解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中12∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)∴ ∠ABC=45 °.选DD1 14、已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
例3 已知AD ∥BC , ∠1=∠2, ∠3=∠4, 直线DC过点E交AD于D,交BC于C.求证:AD+BC=AB点评:证明一条线段是其它两条线段的和,一般可在较长线段上截一线段,使它与两条线段中的一条相等,再证剩下的线段与另一段相等,这种方法叫截长法;或将两线段中的一条延长,使延长部分等于另一线段,再证它与较长线段相等,这种方法叫补短法。证明:在AB上截取AF=AD,连结EF.∴ ΔA FE≌ΔABE∴ ∠AFE=∠D又∵ AD//BC∴ ∠C+∠D= 180°∴ ΔBFE ≌ ΔBCE∵ AD=AF,∠1=∠2,AE=AE而 ∠BFE+∠AFE= 180°∴ ∠C=∠BFE又∵ ∠3=∠4,BE=BE∴ BF=BC∴ AD+BC=AB118. 如图,AB=DE,AF=CD,EF=BC,∠A=∠D,
试说明:BF∥CE 119.如图,AB=DC,
AC=DB, 你能说明图中∠1=∠2的理由吗?120.如图,AB∥DC,AD∥BC,
说出△ABD≌ △CDB的理由。121.如图AB=CD,AD=BC,O为AD中点,过O点的直线分别交AD、BC于M、N,你能说明∠1=∠2吗?122如图AB=AC,∠B=∠C,
点D、E在BC上,且BD= CE,
那么图中又哪些三角形全等?说明理由。1感悟与反思:1、平行——角相等;
2、对顶角——角相等;
3、公共角——角相等;
4、角平分线——角相等;
5、垂直——角相等;
6、中点——边相等;
7、公共边——边相等;
8、旋转——角相等,边相等。1一.挖掘“隐含条件”判全等二.添条件判全等三.转化“间接条件”判全等
全等三角形的 、 也对应相等。判定: 、 、 、 。全等三角形的画图: 利用直尺和圆规,根据 、 、 的方法都可画出与已知三角形全等的三角形。 1三角形全等的4个种判定公理: ABDABCSSA不能判定全等谈谈本节课你有什么收获?你会证明三角形全等了吗?
例1 :如图,点B在AE上,
∠CAB=∠DAB,要使
ΔABC≌ΔABD,可补充的
一个条件是 .分析:现在我们已知 A→∠CAB=∠DAB①用SAS,需要补充条件AB=AC, ②用ASA,需要补充条件∠CBA=∠DBA, ③用AAS,需要补充条件∠C=∠D, ④此外,补充条件∠CBE=∠DBE也可以(?) SASASAAASS→ AB=AB(公共边) .AB=AC ∠CBA=∠DBA∠C=∠D∠CBE=∠DBE1 例、如图,已知AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠1=∠2,试说明:(1) △ABE ≌ △ACD (2)AM=AN
创造条件! ?1练一练一、挖掘“隐含条件”判全等20°5cm3cm学习提示:公共边,公共角,
对顶角这些都是隐含的边,角相等的条件!1
4、如图,已知AD平分∠BAC,
要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 ;AB=AC∠BDA=∠CDA∠B=∠C友情提示:添加条件的题目.首先要
找到已具备的条件,这些条件有些是
题目已知条件 ,有些是图中隐含条件.二.添条件判全等1试一试 三、熟练转化“间接条件”判全等解答解答解答1 6.如图(4)AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?解:∵AE=CF(已知)ADBCFE∴AE-FE=CF-EF(等量减等量,差相等)即AF=CE在△AFD和△CEB中,
∴△AFD≌△CEB(SAS)1解:∵ ∠CAE=∠BAD(已知)∴ ∠CAE+∠BAE=∠BAD+∠BAE
(等量加等量,和相等)即∠BAC=∠DAE在△ABC和△ADE中, ∴△ABC≌ △ADE(AAS)例6 :如图,已知,AB=CD,
CE=DF,AE=BF,
则AE∥DF吗?为什么?证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD. ∴ ΔACE≌ΔBDF(SSS)在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知) ∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)1
实际运用
9. 测量如图河的宽度,某人在河的对岸找到一参照物树木A,视线 AB与河岸垂直,然后该人沿河岸步行10步(每步约0.75M)到O处,进行标记,再向前步行10步到D处,最后背对河岸向前步行20步,此时树木A,标记O,恰好在同一视线上,则河的宽度为 米。
15ABODC 如图是用两根长度相等的拉线固定电线杆的示意图.其中一根拉到B,另一根拉到C。那么C、B两端点到D的距离DC和DB的大小有何关系?说明理由。练一练 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。 AC=DC?
∠ACB=∠DCE
BC=EC △ACB≌△DCE(SAS)
AB=DEECBAD如图线段AB是一个池塘的长度,
现在想测量这个池塘的长度,在
水上测量不方便,你有什么好的
方法较方便地把池塘的长度测量
出来吗?想想看。例8 :如图在 ΔABC中,
AD⊥BC于D,BE⊥AC
于E,AD交BE于F,
若BF=AC,那么∠ABC
的大小是( )A.40° B.50° C.60° D.45°解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中12∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)∴ ∠ABC=45 °.选DD1 14、已知:ΔABC和ΔBDE是等边三角形, 点D在AE的延长线上。
求证:BD + DC = AD
分析:∵AD = AE + ED
∴只需证:BD + DC = AE + ED
∵BD = ED
∴只需证DC = AE即可。
例3 已知AD ∥BC , ∠1=∠2, ∠3=∠4, 直线DC过点E交AD于D,交BC于C.求证:AD+BC=AB点评:证明一条线段是其它两条线段的和,一般可在较长线段上截一线段,使它与两条线段中的一条相等,再证剩下的线段与另一段相等,这种方法叫截长法;或将两线段中的一条延长,使延长部分等于另一线段,再证它与较长线段相等,这种方法叫补短法。证明:在AB上截取AF=AD,连结EF.∴ ΔA FE≌ΔABE∴ ∠AFE=∠D又∵ AD//BC∴ ∠C+∠D= 180°∴ ΔBFE ≌ ΔBCE∵ AD=AF,∠1=∠2,AE=AE而 ∠BFE+∠AFE= 180°∴ ∠C=∠BFE又∵ ∠3=∠4,BE=BE∴ BF=BC∴ AD+BC=AB118. 如图,AB=DE,AF=CD,EF=BC,∠A=∠D,
试说明:BF∥CE 119.如图,AB=DC,
AC=DB, 你能说明图中∠1=∠2的理由吗?120.如图,AB∥DC,AD∥BC,
说出△ABD≌ △CDB的理由。121.如图AB=CD,AD=BC,O为AD中点,过O点的直线分别交AD、BC于M、N,你能说明∠1=∠2吗?122如图AB=AC,∠B=∠C,
点D、E在BC上,且BD= CE,
那么图中又哪些三角形全等?说明理由。1感悟与反思:1、平行——角相等;
2、对顶角——角相等;
3、公共角——角相等;
4、角平分线——角相等;
5、垂直——角相等;
6、中点——边相等;
7、公共边——边相等;
8、旋转——角相等,边相等。1一.挖掘“隐含条件”判全等二.添条件判全等三.转化“间接条件”判全等
