人教版数学八年级下册20.1.1 平均数课件 (共31张PPT)
文档属性
| 名称 | 人教版数学八年级下册20.1.1 平均数课件 (共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 99.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-22 00:00:00 | ||
图片预览










文档简介
课件31张PPT。20.1.1平均数学习目标1.掌握加权平均数公式,理解“权”的含义.2.会用加权平均数解决常见实际问题.复习 概念.一般地,对于n个数x1,x2,…,xn,我们把
叫做这n个数的算术平均数,简称平均数.记为 1.某班5名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童,每人捐款金额如下(单位:元):
10 12 20 48 10
问:这5名同学平均每人捐款多少元?解:这5名同学平均捐款为
(10+12+20+48+10)÷5 = 20(元)
答:这5名同学平均每人捐款20元。此题即是求5位同学捐款金额的算术平均数.分析 2.有两个小组,第一组有2人,数学平均分为90,第二组有30人,数学平均分为70,你能解决下面问题吗? (1)不计算,猜一猜:如果把这两个小组合在一起,每人平均分是接近90还是70?为什么?70(2)你能求出这个平均分到底是多少吗?正确(90+70)÷2=80(分)错误 因为80是 90、70这两个数的平均数,而两个小组合在一起,应求32个数的平均数.即:这种求法对吗?为什么? 实际上,一组数据里的各个数据的“重要程度”未必相同,反映一个数据重要程度的数,我们给它起名叫“权”. 在算数学平均成绩的问题中,2是90的权,30是70的权.某市三个郊县的人数及人均耕地面积如下表: 问:如果求这个市郊县的人均耕地面积,0.15、0.21、0.18对计算结果的影响大小一样吗?试一试 15是0.15的权、7是0.21的权、10是0.18的权.x1, x2,…, xnω1, ω 2,···, ωn数据对应个数n个数x1,x2,…xn的权分别是 ω1, ω 2,···, ω n,一、加权平均数概念叫做这n个(x1,x2,…xn)数的加权平均数.概念:则71.5称为两个数90、70的加权平均数. 0.17称为三个数0.15、0.21、0.18的加权平均数. 权是反映数据重要程度的量,有时用整数来体现某个数据的重要程度,有时用百分数,有时用比值.(90+70)÷2=80(分)是90、70的算术平均数. 当数据的权相等时,加权平均数和算术平均数相等.二、加权平均数的应用例1.某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如下表所示:(1)如果公司认为面试和笔试成绩同样重要,从他们的成绩看,谁将被录取?解(1)甲选手的最后得分为乙选手的最后得分为所以从成绩看应录取甲. 当面试和笔试的成绩按6:4比确定时,应计算两种成绩的加权平均数.分析:(2)如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,面试和笔试的成绩按照6:4的比确定,计算两人各自的平均成绩,看看谁将被录取?(2)甲的平均分为乙的平均分为 所以从成绩看应录取乙. 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50﹪,演讲能力占40 ﹪,演讲效果占10 ﹪的比例,计算选手的综合成绩(百分制). 两名选手的单项成绩如下表所示:请决出两人的名次.练习1解:选手A的最后得分是由上可知选手B获得第一名,选手A获得第二名。选手B的最后得分是例2. 为了了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:这天5路公共汽车平均每班的载客量是多少? 表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?组中值每个小组的两个端点的数的平均数 分析: 频数即是组中值的权 求5路公共汽车平均每班的载客量,即是求组中值的加权平均数.答:这天5路公共汽车平均每班的载客量是73人.数据: 11、 31、 51、 71、 91、 111权: 3、 5、 20、 22、 18、 15练习2.为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树干的周长情况如下图所示,计算这批梧桐树干的平均周长(精确到0.1cm)(2)组中值分别为:分析:(3)用各组的组中值代表各组的实际数据 (1)共有五个小组;棵数分别为: 因此这批法国梧桐树干的平均周长约为60.8 cm .数据棵数(权) 种菜能手李大叔种植了一批新品种黄瓜。为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形统计图。请估计这个新品种黄瓜平均每株结多少根黄瓜。练习3共有4种数据频数(权)分别为分析:解: 因此这个新品种黄瓜平均每株结13根黄瓜.共有4种数据频数分别为三 小结3.求平均数时,如果数据分成小组,统计中常用组中值代表各组的实际数据,计算组中值的加权平均数.2.算术平均数就是权相等时的加权平均数;1. 权就是数据的重要程度.加权平均数的求法及在生活中的应用.4.实际生活中经常用样本的加权平均数来估计总体的平均数.
叫做这n个数的算术平均数,简称平均数.记为 1.某班5名学生为支援希望工程,将平时积攒的零花钱捐献给贫困地区的失学儿童,每人捐款金额如下(单位:元):
10 12 20 48 10
问:这5名同学平均每人捐款多少元?解:这5名同学平均捐款为
(10+12+20+48+10)÷5 = 20(元)
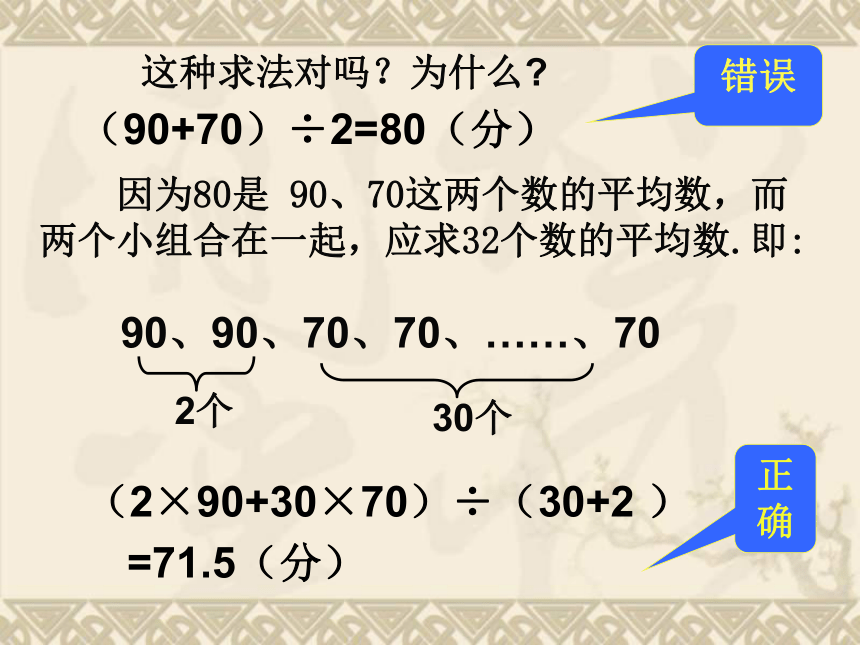
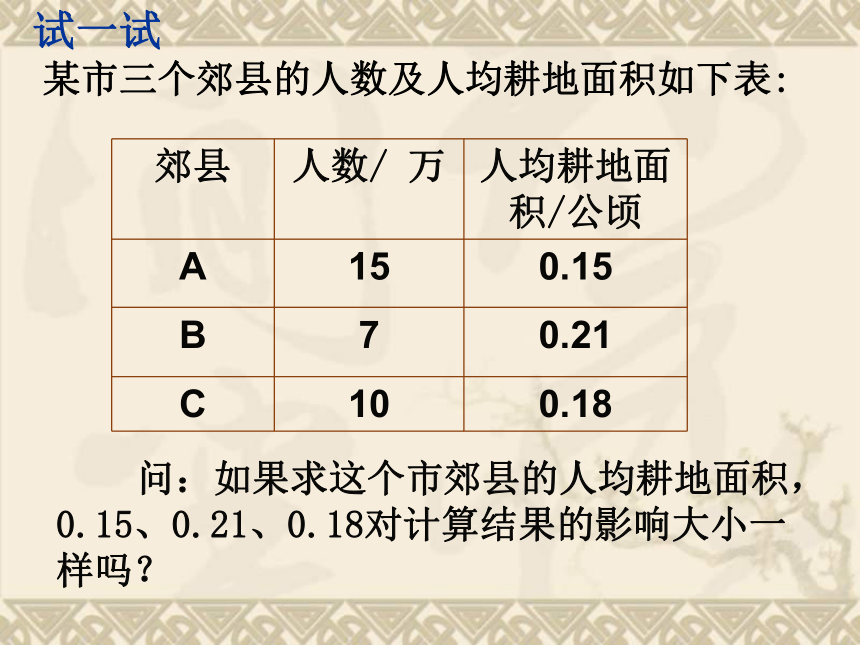
答:这5名同学平均每人捐款20元。此题即是求5位同学捐款金额的算术平均数.分析 2.有两个小组,第一组有2人,数学平均分为90,第二组有30人,数学平均分为70,你能解决下面问题吗? (1)不计算,猜一猜:如果把这两个小组合在一起,每人平均分是接近90还是70?为什么?70(2)你能求出这个平均分到底是多少吗?正确(90+70)÷2=80(分)错误 因为80是 90、70这两个数的平均数,而两个小组合在一起,应求32个数的平均数.即:这种求法对吗?为什么? 实际上,一组数据里的各个数据的“重要程度”未必相同,反映一个数据重要程度的数,我们给它起名叫“权”. 在算数学平均成绩的问题中,2是90的权,30是70的权.某市三个郊县的人数及人均耕地面积如下表: 问:如果求这个市郊县的人均耕地面积,0.15、0.21、0.18对计算结果的影响大小一样吗?试一试 15是0.15的权、7是0.21的权、10是0.18的权.x1, x2,…, xnω1, ω 2,···, ωn数据对应个数n个数x1,x2,…xn的权分别是 ω1, ω 2,···, ω n,一、加权平均数概念叫做这n个(x1,x2,…xn)数的加权平均数.概念:则71.5称为两个数90、70的加权平均数. 0.17称为三个数0.15、0.21、0.18的加权平均数. 权是反映数据重要程度的量,有时用整数来体现某个数据的重要程度,有时用百分数,有时用比值.(90+70)÷2=80(分)是90、70的算术平均数. 当数据的权相等时,加权平均数和算术平均数相等.二、加权平均数的应用例1.某公司欲招聘一名公关人员,对甲、乙两位候选人进行了面试和笔试,他们的成绩如下表所示:(1)如果公司认为面试和笔试成绩同样重要,从他们的成绩看,谁将被录取?解(1)甲选手的最后得分为乙选手的最后得分为所以从成绩看应录取甲. 当面试和笔试的成绩按6:4比确定时,应计算两种成绩的加权平均数.分析:(2)如果公司认为,作为公关人员面试的成绩应该比笔试的成绩更重要,面试和笔试的成绩按照6:4的比确定,计算两人各自的平均成绩,看看谁将被录取?(2)甲的平均分为乙的平均分为 所以从成绩看应录取乙. 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50﹪,演讲能力占40 ﹪,演讲效果占10 ﹪的比例,计算选手的综合成绩(百分制). 两名选手的单项成绩如下表所示:请决出两人的名次.练习1解:选手A的最后得分是由上可知选手B获得第一名,选手A获得第二名。选手B的最后得分是例2. 为了了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表:这天5路公共汽车平均每班的载客量是多少? 表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?组中值每个小组的两个端点的数的平均数 分析: 频数即是组中值的权 求5路公共汽车平均每班的载客量,即是求组中值的加权平均数.答:这天5路公共汽车平均每班的载客量是73人.数据: 11、 31、 51、 71、 91、 111权: 3、 5、 20、 22、 18、 15练习2.为了绿化环境,柳荫街引进一批法国梧桐,三年后这些树干的周长情况如下图所示,计算这批梧桐树干的平均周长(精确到0.1cm)(2)组中值分别为:分析:(3)用各组的组中值代表各组的实际数据 (1)共有五个小组;棵数分别为: 因此这批法国梧桐树干的平均周长约为60.8 cm .数据棵数(权) 种菜能手李大叔种植了一批新品种黄瓜。为了考察这种黄瓜的生长情况,李大叔抽查了部分黄瓜株上长出的黄瓜根数,得到右面的条形统计图。请估计这个新品种黄瓜平均每株结多少根黄瓜。练习3共有4种数据频数(权)分别为分析:解: 因此这个新品种黄瓜平均每株结13根黄瓜.共有4种数据频数分别为三 小结3.求平均数时,如果数据分成小组,统计中常用组中值代表各组的实际数据,计算组中值的加权平均数.2.算术平均数就是权相等时的加权平均数;1. 权就是数据的重要程度.加权平均数的求法及在生活中的应用.4.实际生活中经常用样本的加权平均数来估计总体的平均数.
