高中数学苏教版必修四课时训练:1.3 三角函数的图象和性质1.3.4
文档属性
| 名称 | 高中数学苏教版必修四课时训练:1.3 三角函数的图象和性质1.3.4 |  | |
| 格式 | zip | ||
| 文件大小 | 400.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-23 11:19:06 | ||
图片预览


文档简介
1.3.4 三角函数的应用
课时目标
1.会解三角形和利用三角形建立数学模型,解决实际问题.
2.会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型.
1.三角函数的周期性
y=Asin(ωx+φ)
(ω≠0)的周期是T=________;
y=Acos(ωx+φ)
(ω≠0)的周期是T=________;
y=Atan(ωx+φ)
(ω≠0)的周期是T=________.
2.函数y=Asin(ωx+φ)+k
(A>0,ω>0)的性质
(1)ymax=________,ymin=________
(2)A=________________,k=________________.
(3)ω可由________________确定,其中周期T可观察图象获得.
(4)由ωx1+φ=________,ωx2+φ=________,ωx3+φ=________,ωx4+φ=________,ωx5+φ=________中的一个确定φ的值.
3.三角函数模型的应用
三角函数作为描述现实世界中________现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.
一、填空题
1.
如图所示,单摆从某点开始来回摆动,离开平衡位置O的距离scm和时间ts的函数关系式为s=6sin,那么单摆来回摆动一次所需的时间为________s.
2.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+b的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)=______.
3.函数y=2sin的最小正周期在内,则正整数m的值是________.
4.设某人的血压满足函数式p(t)=115+25sin(160πt),其中p(t)为血压(mmHg),t为时间(min),则此人每分钟心跳的次数是________.
5.一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式时s=3cos,其中g是重力加速度,当小球摆动的周期是1s时,线长l等于______.
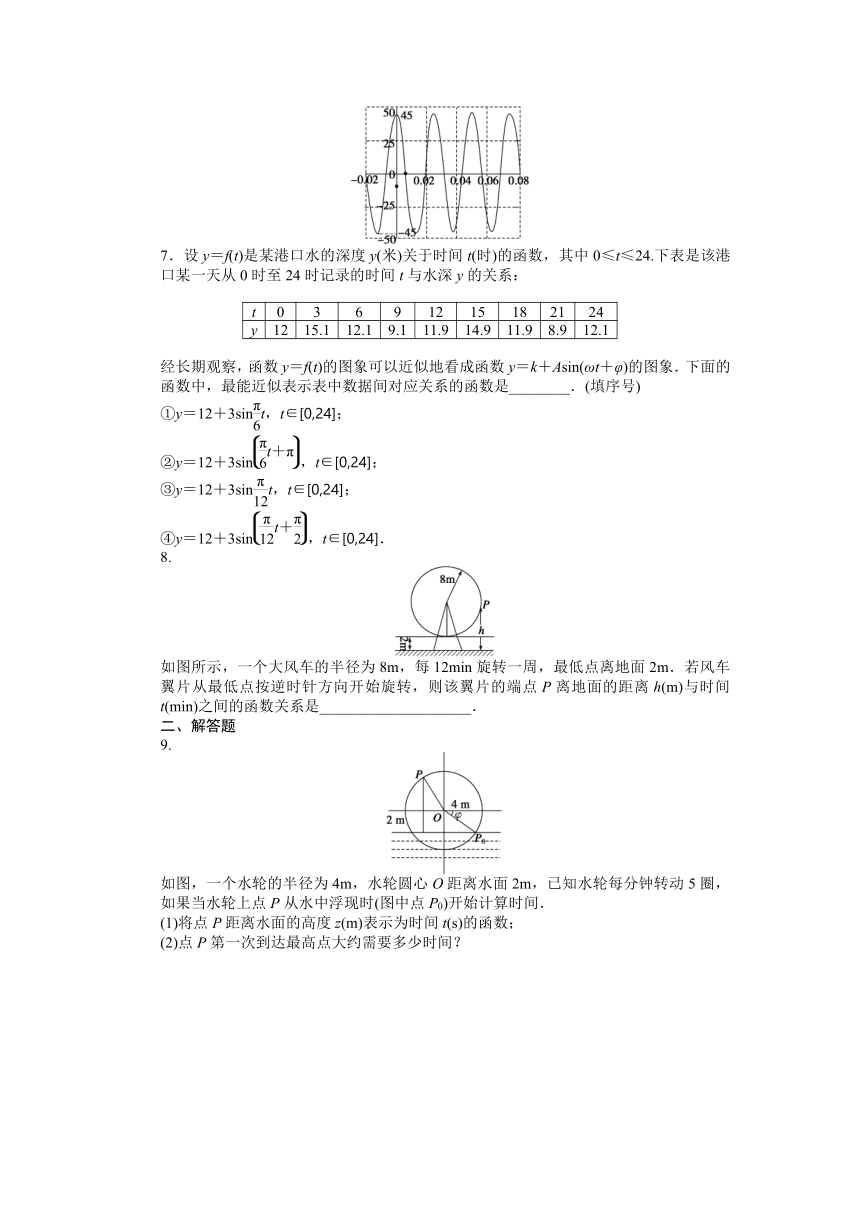
6.如图是一个示波器显示的由简易发电机产生的交流电的电压的变化,则电压V关于时间t的函数关系式为________.
7.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t
0
3
6
9
12
15
18
21
24
y
12
15.1
12.1
9.1
11.9
14.9
11.9
8.9
12.1
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是________.(填序号)
①y=12+3sint,t∈[0,24];
②y=12+3sin,t∈[0,24];
③y=12+3sint,t∈[0,24];
④y=12+3sin,t∈[0,24].
8.
如图所示,一个大风车的半径为8m,每12min旋转一周,最低点离地面2m.若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(m)与时间t(min)之间的函数关系是____________________.
二、解答题
9.
如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
10.某港口水深y(米)是时间t
(0≤t≤24,单位:小时)的函数,下面是水深数据:
t(小时)
0
3
6
9
12
15
18
21
24
y(米)
10.0
13.0
9.9
7.0
10.0
13.0
10.1
7.0
10.0
据上述数据描成的曲线如图所示,经拟合,该曲线可近似的看成正弦函数型y=Asinωt+B的图象.
(1)试根据数据表和曲线,求出y=Asinωt+B的解析式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间?(忽略离港所用的时间)
能力提升
11.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,-),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为________.(填序号)
12.某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=__________,其中t∈[0,60].
1.三角函数模型是研究周期现象最重要的数学模型.三角函数模型在研究物理、生物、自然界中的周期现象(运动)有着广泛的应用.
2.三角函数模型构建的步骤
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
1.3.4 三角函数的应用
知识梳理
1.
2.(1)A+k -A+k
(2)
(3)ω=
(4)0 π π 2π
3.周期
作业设计
1.
2.2sin+7(1≤x≤12,x∈N
)
3.26,27,28
解析 ∵T=,又∵<<,
∴8π∴m=26,27,28.
4.80
解析 T==(分),f==80(次/分).
5.
解析 T==1,∴=2π,∴l=.
6.V=45cos80πt
解析 设V=Acosωt,则A=45,T==0.025,ω==80π,故V=45cos80πt.
7.①
解析 在给定的四个函数①②③④中我们不妨代入t=0及t=3,容易看出最能近似表示表中数据间对应关系的函数是①.
8.h=-8cost+10(t≥0)
解析 据题意可设h=10-8cosωt(t≥0).
由已知周期为12min,可知t=6时到达最高点,即函数取最大值,知18=10-8cos6ω,即cos6ω=-1.
∴6ω=π,得ω=.∴h=10-8cost(t≥0).
9.解 (1)如图所示建立直角坐标系,
设角φ是以Ox为始边,OP0为终边的角.
OP每秒钟内所转过的角为
=.
由OP在时间t(s)内所转过的角为t=t.
由题意可知水轮逆时针转动,
得z=4sin+2.
当t=0时,z=0,得sinφ=-,即φ=-.
故所求的函数关系式为z=4sin+2.
(2)令z=4sin+2=6,
得sin=1,
令t-=,得t=4,
故点P第一次到达最高点大约需要4s.
10.解 (1)从拟合的曲线可知,函数y=Asinωt+B的一个周期为12小时,因此ω==.
又ymin=7,ymax=13,∴A=(ymax-ymin)=3,
B=(ymax+ymin)=10.
∴函数的解析式为y=3sint+10
(0≤t≤24).
(2)由题意,水深y≥4.5+7,
即y=3sint+10≥11.5,t∈[0,24],
∴sint≥,t∈,k=0,1,
∴t∈[1,5]或t∈[13,17],
所以,该船在1∶00至5∶00或13∶00至17∶00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
11.③
解析 ∵P0(,-),∴∠P0Ox=.
按逆时针转时间t后得∠POP0=t,∠POx=t-,此时P点纵坐标为2sin(t-),
∴d=2|sin(t-)|.
当t=0时,d=,排除①④;
当t=时,d=0,排除②.
12.10sin
解析 将解析式可写为d=Asin(ωt+φ)形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,
可得ω=,所以d=10sin.
课时目标
1.会解三角形和利用三角形建立数学模型,解决实际问题.
2.会用三角函数解决一些简单的实际问题,体会三角函数是描述周期变化现象的重要函数模型.
1.三角函数的周期性
y=Asin(ωx+φ)
(ω≠0)的周期是T=________;
y=Acos(ωx+φ)
(ω≠0)的周期是T=________;
y=Atan(ωx+φ)
(ω≠0)的周期是T=________.
2.函数y=Asin(ωx+φ)+k
(A>0,ω>0)的性质
(1)ymax=________,ymin=________
(2)A=________________,k=________________.
(3)ω可由________________确定,其中周期T可观察图象获得.
(4)由ωx1+φ=________,ωx2+φ=________,ωx3+φ=________,ωx4+φ=________,ωx5+φ=________中的一个确定φ的值.
3.三角函数模型的应用
三角函数作为描述现实世界中________现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.
一、填空题
1.
如图所示,单摆从某点开始来回摆动,离开平衡位置O的距离scm和时间ts的函数关系式为s=6sin,那么单摆来回摆动一次所需的时间为________s.
2.据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+φ)+b的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)=______.
3.函数y=2sin的最小正周期在内,则正整数m的值是________.
4.设某人的血压满足函数式p(t)=115+25sin(160πt),其中p(t)为血压(mmHg),t为时间(min),则此人每分钟心跳的次数是________.
5.一根长lcm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式时s=3cos,其中g是重力加速度,当小球摆动的周期是1s时,线长l等于______.
6.如图是一个示波器显示的由简易发电机产生的交流电的电压的变化,则电压V关于时间t的函数关系式为________.
7.设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
t
0
3
6
9
12
15
18
21
24
y
12
15.1
12.1
9.1
11.9
14.9
11.9
8.9
12.1
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是________.(填序号)
①y=12+3sint,t∈[0,24];
②y=12+3sin,t∈[0,24];
③y=12+3sint,t∈[0,24];
④y=12+3sin,t∈[0,24].
8.
如图所示,一个大风车的半径为8m,每12min旋转一周,最低点离地面2m.若风车翼片从最低点按逆时针方向开始旋转,则该翼片的端点P离地面的距离h(m)与时间t(min)之间的函数关系是____________________.
二、解答题
9.
如图,一个水轮的半径为4m,水轮圆心O距离水面2m,已知水轮每分钟转动5圈,如果当水轮上点P从水中浮现时(图中点P0)开始计算时间.
(1)将点P距离水面的高度z(m)表示为时间t(s)的函数;
(2)点P第一次到达最高点大约需要多少时间?
10.某港口水深y(米)是时间t
(0≤t≤24,单位:小时)的函数,下面是水深数据:
t(小时)
0
3
6
9
12
15
18
21
24
y(米)
10.0
13.0
9.9
7.0
10.0
13.0
10.1
7.0
10.0
据上述数据描成的曲线如图所示,经拟合,该曲线可近似的看成正弦函数型y=Asinωt+B的图象.
(1)试根据数据表和曲线,求出y=Asinωt+B的解析式;
(2)一般情况下,船舶航行时船底与海底的距离不小于4.5米是安全的,如果某船的吃水度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,它在港内停留的时间最多不能超过多长时间?(忽略离港所用的时间)
能力提升
11.如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,-),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为________.(填序号)
12.某时钟的秒针端点A到中心点O的距离为5cm,秒针均匀地绕点O旋转,当时间t=0时,点A与钟面上标12的点B重合,将A、B两点的距离d(cm)表示成t(s)的函数,则d=__________,其中t∈[0,60].
1.三角函数模型是研究周期现象最重要的数学模型.三角函数模型在研究物理、生物、自然界中的周期现象(运动)有着广泛的应用.
2.三角函数模型构建的步骤
(1)收集数据,观察数据,发现是否具有周期性的重复现象.
(2)制作散点图,选择函数模型进行拟合.
(3)利用三角函数模型解决实际问题.
(4)根据问题的实际意义,对答案的合理性进行检验.
1.3.4 三角函数的应用
知识梳理
1.
2.(1)A+k -A+k
(2)
(3)ω=
(4)0 π π 2π
3.周期
作业设计
1.
2.2sin+7(1≤x≤12,x∈N
)
3.26,27,28
解析 ∵T=,又∵<<,
∴8π
4.80
解析 T==(分),f==80(次/分).
5.
解析 T==1,∴=2π,∴l=.
6.V=45cos80πt
解析 设V=Acosωt,则A=45,T==0.025,ω==80π,故V=45cos80πt.
7.①
解析 在给定的四个函数①②③④中我们不妨代入t=0及t=3,容易看出最能近似表示表中数据间对应关系的函数是①.
8.h=-8cost+10(t≥0)
解析 据题意可设h=10-8cosωt(t≥0).
由已知周期为12min,可知t=6时到达最高点,即函数取最大值,知18=10-8cos6ω,即cos6ω=-1.
∴6ω=π,得ω=.∴h=10-8cost(t≥0).
9.解 (1)如图所示建立直角坐标系,
设角φ是以Ox为始边,OP0为终边的角.
OP每秒钟内所转过的角为
=.
由OP在时间t(s)内所转过的角为t=t.
由题意可知水轮逆时针转动,
得z=4sin+2.
当t=0时,z=0,得sinφ=-,即φ=-.
故所求的函数关系式为z=4sin+2.
(2)令z=4sin+2=6,
得sin=1,
令t-=,得t=4,
故点P第一次到达最高点大约需要4s.
10.解 (1)从拟合的曲线可知,函数y=Asinωt+B的一个周期为12小时,因此ω==.
又ymin=7,ymax=13,∴A=(ymax-ymin)=3,
B=(ymax+ymin)=10.
∴函数的解析式为y=3sint+10
(0≤t≤24).
(2)由题意,水深y≥4.5+7,
即y=3sint+10≥11.5,t∈[0,24],
∴sint≥,t∈,k=0,1,
∴t∈[1,5]或t∈[13,17],
所以,该船在1∶00至5∶00或13∶00至17∶00能安全进港.
若欲于当天安全离港,它在港内停留的时间最多不能超过16小时.
11.③
解析 ∵P0(,-),∴∠P0Ox=.
按逆时针转时间t后得∠POP0=t,∠POx=t-,此时P点纵坐标为2sin(t-),
∴d=2|sin(t-)|.
当t=0时,d=,排除①④;
当t=时,d=0,排除②.
12.10sin
解析 将解析式可写为d=Asin(ωt+φ)形式,由题意易知A=10,当t=0时,d=0,得φ=0;当t=30时,d=10,
可得ω=,所以d=10sin.
