黑龙江大庆五十六中2016-2017九年级(五四学制)下第三次月考数学试题(含答案)
文档属性
| 名称 | 黑龙江大庆五十六中2016-2017九年级(五四学制)下第三次月考数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 374.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-23 00:00:00 | ||
图片预览




文档简介
初四年级下学期第三次质量检测
数
学
试
题
出题人:数学组
注意:1、全卷共4
页28
题;
总分120
分;2、请用黑色墨水笔在答题卡书写作答
一、选择题(本大题共10小题,每小题3分,共30分)
1.我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学记数法表示为(
)
A、
B、
C、
D、
2.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是(
)
A.﹣2a+b
B.2a﹣b
C.﹣b
D.b
3.下列命题是假命题的是(
)
A.经过两点有且只有一条直线
(2题图)
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径
4.关于x的一元二次方程
有两个相等的实数根,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
5.在配紫色游戏中,转盘被平均分成“红”、“黄”、“蓝”、“白”四部分,转动转盘两次,配成紫色的概率为(
)
A.
B.
C.
D.
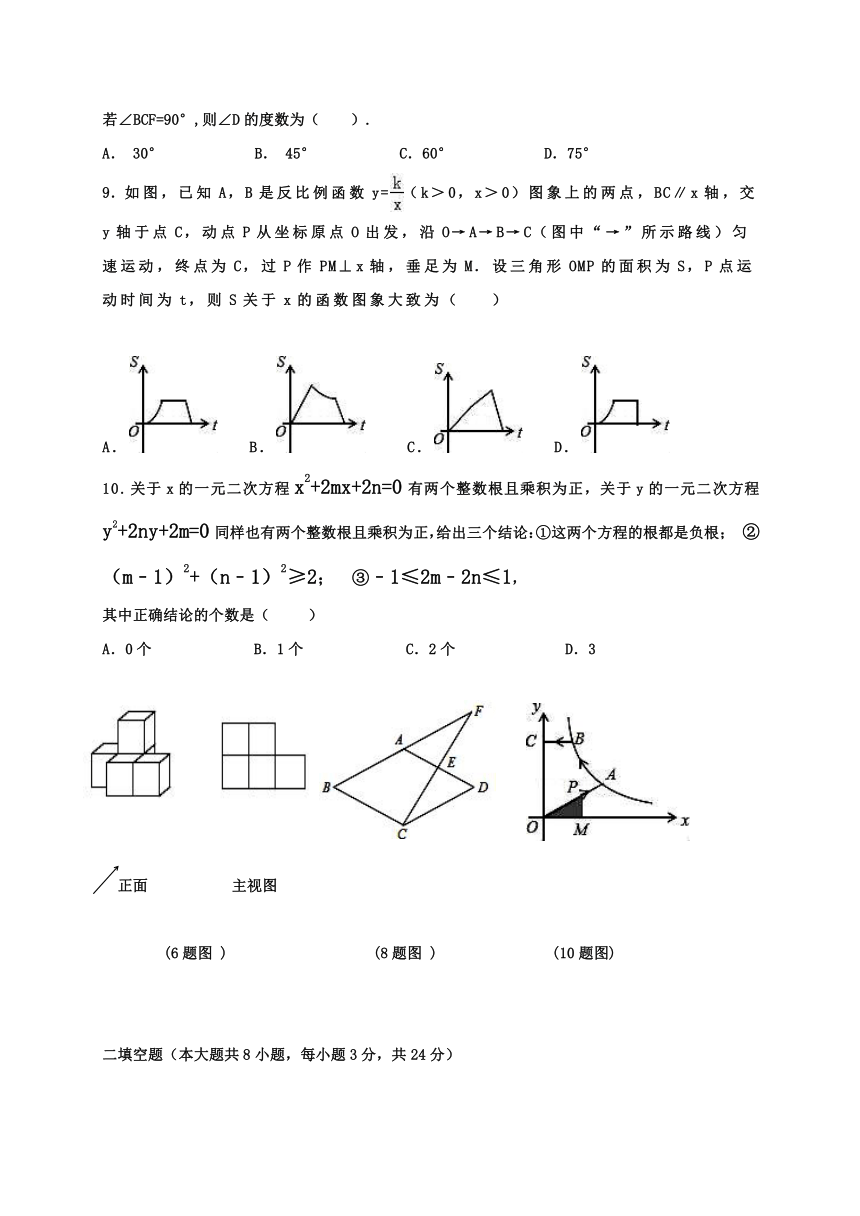
6.如图,左边是一个由5个棱长为1的小正方体组合成的几何体,现在增加一个小正方体,使其主视图如右图,则增加后的几何体的左视图的面积为(
).
A.3
B.
4
C.
5
D.6
7.大自然中存在很多轴对称现象,下列植物叶子图案中既是轴对称图形,又是中心对称图形的是(
)
如图,菱形ABCD中,点E是AD的中点,连接CE,并延长CE与BA的延长线交于点F,
若∠BCF=90°,则∠D的度数为(
).
A.
30°
B.
45°
C.60°
D.75°
9.如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为(
)
A.
B.
C.
D.
10.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都是负根;
②(m﹣1)2+(n﹣1)2≥2;
③﹣1≤2m﹣2n≤1,
其中正确结论的个数是(
)
A.0个
B.1个
C.2个
D.3
正面
主视图
(6题图
)
(8题图
)
(10题图)
二填空题(本大题共8小题,每小题3分,共24分)
11.函数的自变量x的取值范围是
.
12.若3x2nym与x4﹣nyn﹣1是同类项,则m+n=
.
13.已知一组数据-3,x,-2,3,1,6的中位数是1,则其方差为
.
14.如图,△ABC是边长为4个等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为
(结果保留π).
15.如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=,则AF的长度为=
.
16.已知∠AOB=60°,点P到射线OA,OB的距离分别为2和,垂足分别为M、N,则ON的长为
.
在平面直角坐标系中,直线
与x轴交于点A1,如图所示依次作正方形
A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…
在直线
上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .
18.如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),
过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点
分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和
为
(14题图
)
(15题图
)
(17题图)
(18题图
)
三、解答题(本大题共10小题,共66分)
19.计算:
20.化简求值: ,其中a=3+,b=3﹣.
21.为响应低碳号召,肖老师上班的交通方式由自驾车改为骑自行车,肖老师家距学校15千米,因为自驾车的速度是骑自行车速度的4倍,所以肖老师每天比原来早出发45分钟,才能按原时间到校,求肖老师骑自行车每小时走多少千米.
如果关于x的不等(2m﹣n)x+m﹣5n>0的解集为x<,
试求关于x的不等式mx>n的解集.
23.某市2015年国民经济和社会发展统计公报显示,2015年该市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题:
(1)求经济适用房的套数,并补全图1;
(2)假如申请购买经济适用房的对象中共有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2015年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果计划2017年新开工廉租房建设的套数要达到720套,那么2016~2017这两年新开工廉租房的套数的年平均增长率是多少?
24.在如图所示的一张矩形纸片ABCD(AD>AB)中,将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:2AE2=AC AP;
(3)若AE=8cm,△ABF的面积为9cm2,求△ABF的周长.
25.小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据≈1.41,≈1.73供选用,结果保留整数)
26.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
27.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:AE FD=AF EC;
(2)求证:FC=FB;
(3)若FB=FE=2,求⊙O的半径r的长.
已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,
点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.
(1)求二次函数解析式;
(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.
②设△DEF与△ABC重叠部分的面积为S,直接写出S关于t的函数关系式;
初四下学期第三次质量检测
数学参考答案
1~5:AACBD,6~10:ADCAD
12、
13、9
14、
15、
16、5或3
17、
18、
19、6
20、,
21、解:设肖老师骑自行车每小时走x千米.
根据题意得:,
解得x=15,
经检验x=15是原方程的解,并符合实际意义,
答:肖老师骑自行车每小时走15千米.
22、解:移项得(2m﹣n)x>5n﹣m,
∵关于x的不等(2m﹣n)x+m﹣5n>0的解集为x<,
∴2m﹣n<0,且x<,
∴=,
整理得n=m,
把n=m代入2m﹣n<0得,
2m﹣m<0,解得m<0,
∵mx>n,
∴mx>m,
∴x<.
∴关于x的不等式mx>n的解集是x<.
23、解:(1)1500÷24%=6250
6250×7.6%=475
所以经济适用房的套数有475套;
如图所示:
(2)老王被摇中的概率为:;
(3)设2013~2014这两年新开工廉租房的套数的年平均增长率为x
因为2012年廉租房共有6250×8%=500(套)
所以依题意,得
500(1+x)2=720…(7分)
解这个方程得,x1=0.2,x2=﹣2.2(不合题意,舍去)
答:这两年新开工廉租房的套数的年平均增长率为20%.
24、解:(1)连接EF交AC于O,
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF.
∴OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴平行四边形AFCE是菱形.
(2)证明:过E作EP⊥AD交AC于P,
由作法,∠AEP=90°,
由(1)知:∠AOE=90°,又∠EAO=∠EAP,
∴△AOE∽△AEP,
∴,则AE2=AO AP,
∵四边形AFCE是菱形,
∴,
∴.
∴2AE2=AC AP.
(3)∵四边形AFCE是菱形,
∴AF=AE=8.
设AB=x,BF=y,
∵∠B=90,即三角形ABC为直角三角形,
∴x2+y2=64,
∴(x+y)2﹣2xy=64①,
又∵S△ABF=9,∴,则xy=18②,
由①、②得:(x+y)2=100,
∴x+y=10,x+y=﹣10(不合题意舍去),
∴△ABF的周长为x+y+AF=10+8=18.
25、解:∵斜坡的坡度是i==,EF=2,
∴FD=2.5EF=2.5×2=5,
∵CE=13,CE=GF,
∴GD=GF+FD=CE+FD=13+5=18,
在Rt△DBG中,∠GDB=45°,
∴BG=GD=18,
在Rt△DAN中,∠NDA=60°,
∴ND=NG+GD=CH+GD=2+18=20,
AN=ND tan60°=20×=20,
∴AM=AN﹣MN=AN﹣BG=20﹣18≈17(米).
答:铁塔高AM约17米.
26、解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,
即m=﹣n,
则A(2,﹣n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
∵A(2,﹣n),B(n,﹣2),
∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,
∵S△ABC=S梯形BCAD﹣S△BDA=5,
∴×(2﹣n+2)×2﹣×(2﹣n)×(﹣n+2),
解得:n=﹣3,
即A(2,3),B(﹣3,﹣2),
把A(2,3)代入y=得:k2=6,
即反比例函数的解析式是y=;
把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,
解得:k1=1,b=1,
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴不等式k1x+b>的解集是﹣3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0,
即P的取值范围是p≤﹣2或p>0.
27、(1)证明:∵BD是⊙O的切线,
∴∠DBA=90°,
∵CH⊥AB,
∴CH∥BD,
∴△AEC∽△AFD,
∴=,
∴AE FD=AF EC.
(2)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴==,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(3)解:∵BF=CF=DF(已证),EF=BF=2,
∴EF=FC,
∴∠FCE=∠FEC,
∵∠AHE=∠CHG=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵BF切⊙O于B,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CG,
∴CG是⊙O切线,
由△GCB∽△GAC得
GC2=BG×AG
∵AB=BG,
FB=FE=2,
∴(2+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理,得:BG2=FG2﹣BF2,
∴FG2﹣4FG﹣12=0,
解得:FG=6,FG=﹣2(舍去),
由勾股定理得:
AB=BG==4,
∴⊙O的半径是2.
28、解:(1)由题意得
解得:a=,b=﹣.
(2)①由(1)知二次函数为y=x2﹣x﹣2
∵A(4,0),∴B(﹣1,0),C(0,﹣2)
∴OA=4,OB=1,OC=2
∴AB=5,AC=2,BC=
∴AC2+BC2=25=AB2
∴△ABC为直角三角形,且∠ACB=90°
∵AE=2t,AF=t,∴==
又∵∠EAF=∠CAB,∴△AEF∽△ACB
∴∠AEF=∠ACB=90°
∴△AEF沿EF翻折后,点A落在x轴上点D处;
由翻折知,DE=AE,∴AD=2AE=4t,EF=AE=t
假设△DCF为直角三角形
当点F在线段AC上时
ⅰ)若C为直角顶点,则点D与点B重合,如图2
∴AE=AB=
t=÷2=;
ⅱ)若D为直角顶点,如图3
∵∠CDF=90°,∴∠ODC+∠EDF=90°
∵∠EDF=∠EAF,∴∠OBC+∠EAF=90°
∴∠ODC=∠OBC,∴BC=DC
∵OC⊥BD,∴OD=OB=1
∴AD=3,∴AE=
∴t=;
当点F在AC延长线上时,∠DFC>90°,△DCF为钝角三角形
综上所述,存在时刻t,使得△DCF为直角三角形,t=或t=.
②ⅰ)当0<t≤时,重叠部分为△DEF,如图1、图2
∴S=×2t×t=t2;
ⅱ)当<t≤2时,设DF与BC相交于点G,则重叠部分为四边形BEFG,如图4
过点G作GH⊥BE于H,设GH=a
则BH=,DH=2a,∴DB=
∵DB=AD﹣AB=4t﹣5
∴=4t﹣5,∴a=(4t﹣5)
∴S=S△DEF﹣S△DBG=×2t×t﹣(4t﹣5)×(4t﹣5)=﹣t2+t﹣;
ⅲ)当2<t≤时,重叠部分为△BEG,如图5
∵BE=DE﹣DB=2t﹣(4t﹣5)=5﹣2t,GE=2BE=2(5﹣2t)
∴S=×(5﹣2t)×2(5﹣2t)=4t2﹣20t+25.
数
学
试
题
出题人:数学组
注意:1、全卷共4
页28
题;
总分120
分;2、请用黑色墨水笔在答题卡书写作答
一、选择题(本大题共10小题,每小题3分,共30分)
1.我国第六次人口普查显示,全国人口为1370536875人,将这个总人口数(保留三个有效数字)用科学记数法表示为(
)
A、
B、
C、
D、
2.实数a,b在数轴上对应点的位置如图所示,化简|a|+的结果是(
)
A.﹣2a+b
B.2a﹣b
C.﹣b
D.b
3.下列命题是假命题的是(
)
A.经过两点有且只有一条直线
(2题图)
B.三角形的中位线平行且等于第三边的一半
C.平行四边形的对角线相等
D.圆的切线垂直于经过切点的半径
4.关于x的一元二次方程
有两个相等的实数根,则锐角α等于( )
A.15°
B.30°
C.45°
D.60°
5.在配紫色游戏中,转盘被平均分成“红”、“黄”、“蓝”、“白”四部分,转动转盘两次,配成紫色的概率为(
)
A.
B.
C.
D.
6.如图,左边是一个由5个棱长为1的小正方体组合成的几何体,现在增加一个小正方体,使其主视图如右图,则增加后的几何体的左视图的面积为(
).
A.3
B.
4
C.
5
D.6
7.大自然中存在很多轴对称现象,下列植物叶子图案中既是轴对称图形,又是中心对称图形的是(
)
如图,菱形ABCD中,点E是AD的中点,连接CE,并延长CE与BA的延长线交于点F,
若∠BCF=90°,则∠D的度数为(
).
A.
30°
B.
45°
C.60°
D.75°
9.如图,已知A,B是反比例函数y=(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于x的函数图象大致为(
)
A.
B.
C.
D.
10.关于x的一元二次方程x2+2mx+2n=0有两个整数根且乘积为正,关于y的一元二次方程y2+2ny+2m=0同样也有两个整数根且乘积为正,给出三个结论:①这两个方程的根都是负根;
②(m﹣1)2+(n﹣1)2≥2;
③﹣1≤2m﹣2n≤1,
其中正确结论的个数是(
)
A.0个
B.1个
C.2个
D.3
正面
主视图
(6题图
)
(8题图
)
(10题图)
二填空题(本大题共8小题,每小题3分,共24分)
11.函数的自变量x的取值范围是
.
12.若3x2nym与x4﹣nyn﹣1是同类项,则m+n=
.
13.已知一组数据-3,x,-2,3,1,6的中位数是1,则其方差为
.
14.如图,△ABC是边长为4个等边三角形,D为AB边的中点,以CD为直径画圆,则图中阴影部分的面积为
(结果保留π).
15.如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=,则AF的长度为=
.
16.已知∠AOB=60°,点P到射线OA,OB的距离分别为2和,垂足分别为M、N,则ON的长为
.
在平面直角坐标系中,直线
与x轴交于点A1,如图所示依次作正方形
A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…
在直线
上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .
18.如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O、A),
过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点
分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和
为
(14题图
)
(15题图
)
(17题图)
(18题图
)
三、解答题(本大题共10小题,共66分)
19.计算:
20.化简求值: ,其中a=3+,b=3﹣.
21.为响应低碳号召,肖老师上班的交通方式由自驾车改为骑自行车,肖老师家距学校15千米,因为自驾车的速度是骑自行车速度的4倍,所以肖老师每天比原来早出发45分钟,才能按原时间到校,求肖老师骑自行车每小时走多少千米.
如果关于x的不等(2m﹣n)x+m﹣5n>0的解集为x<,
试求关于x的不等式mx>n的解集.
23.某市2015年国民经济和社会发展统计公报显示,2015年该市新开工的住房有商品房、廉租房、经济适用房和公共租赁房四种类型.老王对这四种新开工的住房套数和比例进行了统计,并将统计结果绘制成下面两幅统计图,请你结合图中所给信息解答下列问题:
(1)求经济适用房的套数,并补全图1;
(2)假如申请购买经济适用房的对象中共有950人符合购买条件,老王是其中之一.由于购买人数超过房子套数,购买者必须通过电脑摇号产生.如果对2015年新开工的经济适用房进行电脑摇号,那么老王被摇中的概率是多少?
(3)如果计划2017年新开工廉租房建设的套数要达到720套,那么2016~2017这两年新开工廉租房的套数的年平均增长率是多少?
24.在如图所示的一张矩形纸片ABCD(AD>AB)中,将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE.
(1)求证:四边形AFCE是菱形;
(2)过E作EP⊥AD交AC于P,求证:2AE2=AC AP;
(3)若AE=8cm,△ABF的面积为9cm2,求△ABF的周长.
25.小明在数学课中学习了《解直角三角形》的内容后,双休日组织教学兴趣小组的小伙伴进行实地测量.如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米.大家根据所学知识很快计算出了铁塔高AM.亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程.(数据≈1.41,≈1.73供选用,结果保留整数)
26.如图,一次函数y=k1x+b与反比例函数y=的图象交于A(2,m),B(n,﹣2)两点.过点B作BC⊥x轴,垂足为C,且S△ABC=5.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式k1x+b>的解集;
(3)若P(p,y1),Q(﹣2,y2)是函数y=图象上的两点,且y1≥y2,求实数p的取值范围.
27.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:AE FD=AF EC;
(2)求证:FC=FB;
(3)若FB=FE=2,求⊙O的半径r的长.
已知二次函数y=ax2+bx﹣2的图象与x轴交于A、B两点,与y轴交于点C,
点A的坐标为(4,0),且当x=﹣2和x=5时二次函数的函数值y相等.
(1)求二次函数解析式;
(2)如图1,动点E、F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由.
②设△DEF与△ABC重叠部分的面积为S,直接写出S关于t的函数关系式;
初四下学期第三次质量检测
数学参考答案
1~5:AACBD,6~10:ADCAD
12、
13、9
14、
15、
16、5或3
17、
18、
19、6
20、,
21、解:设肖老师骑自行车每小时走x千米.
根据题意得:,
解得x=15,
经检验x=15是原方程的解,并符合实际意义,
答:肖老师骑自行车每小时走15千米.
22、解:移项得(2m﹣n)x>5n﹣m,
∵关于x的不等(2m﹣n)x+m﹣5n>0的解集为x<,
∴2m﹣n<0,且x<,
∴=,
整理得n=m,
把n=m代入2m﹣n<0得,
2m﹣m<0,解得m<0,
∵mx>n,
∴mx>m,
∴x<.
∴关于x的不等式mx>n的解集是x<.
23、解:(1)1500÷24%=6250
6250×7.6%=475
所以经济适用房的套数有475套;
如图所示:
(2)老王被摇中的概率为:;
(3)设2013~2014这两年新开工廉租房的套数的年平均增长率为x
因为2012年廉租房共有6250×8%=500(套)
所以依题意,得
500(1+x)2=720…(7分)
解这个方程得,x1=0.2,x2=﹣2.2(不合题意,舍去)
答:这两年新开工廉租房的套数的年平均增长率为20%.
24、解:(1)连接EF交AC于O,
当顶点A与C重合时,折痕EF垂直平分AC,
∴OA=OC,∠AOE=∠COF=90°
∵在矩形ABCD中,AD∥BC,
∴∠EAO=∠FCO,
∴△AOE≌△COF.
∴OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴平行四边形AFCE是菱形.
(2)证明:过E作EP⊥AD交AC于P,
由作法,∠AEP=90°,
由(1)知:∠AOE=90°,又∠EAO=∠EAP,
∴△AOE∽△AEP,
∴,则AE2=AO AP,
∵四边形AFCE是菱形,
∴,
∴.
∴2AE2=AC AP.
(3)∵四边形AFCE是菱形,
∴AF=AE=8.
设AB=x,BF=y,
∵∠B=90,即三角形ABC为直角三角形,
∴x2+y2=64,
∴(x+y)2﹣2xy=64①,
又∵S△ABF=9,∴,则xy=18②,
由①、②得:(x+y)2=100,
∴x+y=10,x+y=﹣10(不合题意舍去),
∴△ABF的周长为x+y+AF=10+8=18.
25、解:∵斜坡的坡度是i==,EF=2,
∴FD=2.5EF=2.5×2=5,
∵CE=13,CE=GF,
∴GD=GF+FD=CE+FD=13+5=18,
在Rt△DBG中,∠GDB=45°,
∴BG=GD=18,
在Rt△DAN中,∠NDA=60°,
∴ND=NG+GD=CH+GD=2+18=20,
AN=ND tan60°=20×=20,
∴AM=AN﹣MN=AN﹣BG=20﹣18≈17(米).
答:铁塔高AM约17米.
26、解:(1)把A(2,m),B(n,﹣2)代入y=得:k2=2m=﹣2n,
即m=﹣n,
则A(2,﹣n),
过A作AE⊥x轴于E,过B作BF⊥y轴于F,延长AE、BF交于D,
∵A(2,﹣n),B(n,﹣2),
∴BD=2﹣n,AD=﹣n+2,BC=|﹣2|=2,
∵S△ABC=S梯形BCAD﹣S△BDA=5,
∴×(2﹣n+2)×2﹣×(2﹣n)×(﹣n+2),
解得:n=﹣3,
即A(2,3),B(﹣3,﹣2),
把A(2,3)代入y=得:k2=6,
即反比例函数的解析式是y=;
把A(2,3),B(﹣3,﹣2)代入y=k1x+b得:,
解得:k1=1,b=1,
即一次函数的解析式是y=x+1;
(2)∵A(2,3),B(﹣3,﹣2),
∴不等式k1x+b>的解集是﹣3<x<0或x>2;
(3)分为两种情况:当点P在第三象限时,要使y1≥y2,实数p的取值范围是P≤﹣2,
当点P在第一象限时,要使y1≥y2,实数p的取值范围是P>0,
即P的取值范围是p≤﹣2或p>0.
27、(1)证明:∵BD是⊙O的切线,
∴∠DBA=90°,
∵CH⊥AB,
∴CH∥BD,
∴△AEC∽△AFD,
∴=,
∴AE FD=AF EC.
(2)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴==,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(3)解:∵BF=CF=DF(已证),EF=BF=2,
∴EF=FC,
∴∠FCE=∠FEC,
∵∠AHE=∠CHG=90°,
∴∠FAH+∠AEH=90°,∠G+∠GCH=90°,
∵∠AEH=∠CEF,
∴∠G=∠FAG,
∴AF=FG,
∵FB⊥AG,
∴AB=BG,
∵BF切⊙O于B,
∴∠FBC=∠CAB,
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC,
∴∠FCB=∠CAB,
∵∠ACB=90°,
∴∠ACO+∠BCO=90°,
∴∠FCB+∠BCO=90°,
即OC⊥CG,
∴CG是⊙O切线,
由△GCB∽△GAC得
GC2=BG×AG
∵AB=BG,
FB=FE=2,
∴(2+FG)2=BG×AG=2BG2,
在Rt△BFG中,由勾股定理,得:BG2=FG2﹣BF2,
∴FG2﹣4FG﹣12=0,
解得:FG=6,FG=﹣2(舍去),
由勾股定理得:
AB=BG==4,
∴⊙O的半径是2.
28、解:(1)由题意得
解得:a=,b=﹣.
(2)①由(1)知二次函数为y=x2﹣x﹣2
∵A(4,0),∴B(﹣1,0),C(0,﹣2)
∴OA=4,OB=1,OC=2
∴AB=5,AC=2,BC=
∴AC2+BC2=25=AB2
∴△ABC为直角三角形,且∠ACB=90°
∵AE=2t,AF=t,∴==
又∵∠EAF=∠CAB,∴△AEF∽△ACB
∴∠AEF=∠ACB=90°
∴△AEF沿EF翻折后,点A落在x轴上点D处;
由翻折知,DE=AE,∴AD=2AE=4t,EF=AE=t
假设△DCF为直角三角形
当点F在线段AC上时
ⅰ)若C为直角顶点,则点D与点B重合,如图2
∴AE=AB=
t=÷2=;
ⅱ)若D为直角顶点,如图3
∵∠CDF=90°,∴∠ODC+∠EDF=90°
∵∠EDF=∠EAF,∴∠OBC+∠EAF=90°
∴∠ODC=∠OBC,∴BC=DC
∵OC⊥BD,∴OD=OB=1
∴AD=3,∴AE=
∴t=;
当点F在AC延长线上时,∠DFC>90°,△DCF为钝角三角形
综上所述,存在时刻t,使得△DCF为直角三角形,t=或t=.
②ⅰ)当0<t≤时,重叠部分为△DEF,如图1、图2
∴S=×2t×t=t2;
ⅱ)当<t≤2时,设DF与BC相交于点G,则重叠部分为四边形BEFG,如图4
过点G作GH⊥BE于H,设GH=a
则BH=,DH=2a,∴DB=
∵DB=AD﹣AB=4t﹣5
∴=4t﹣5,∴a=(4t﹣5)
∴S=S△DEF﹣S△DBG=×2t×t﹣(4t﹣5)×(4t﹣5)=﹣t2+t﹣;
ⅲ)当2<t≤时,重叠部分为△BEG,如图5
∵BE=DE﹣DB=2t﹣(4t﹣5)=5﹣2t,GE=2BE=2(5﹣2t)
∴S=×(5﹣2t)×2(5﹣2t)=4t2﹣20t+25.
同课章节目录
