2017年高考备考“最后30天”大冲刺+数学+专题一+三视图(文)+教师版+Word版含解析】
文档属性
| 名称 | 2017年高考备考“最后30天”大冲刺+数学+专题一+三视图(文)+教师版+Word版含解析】 |
|
|
| 格式 | zip | ||
| 文件大小 | 940.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-24 00:00:00 | ||
图片预览



文档简介
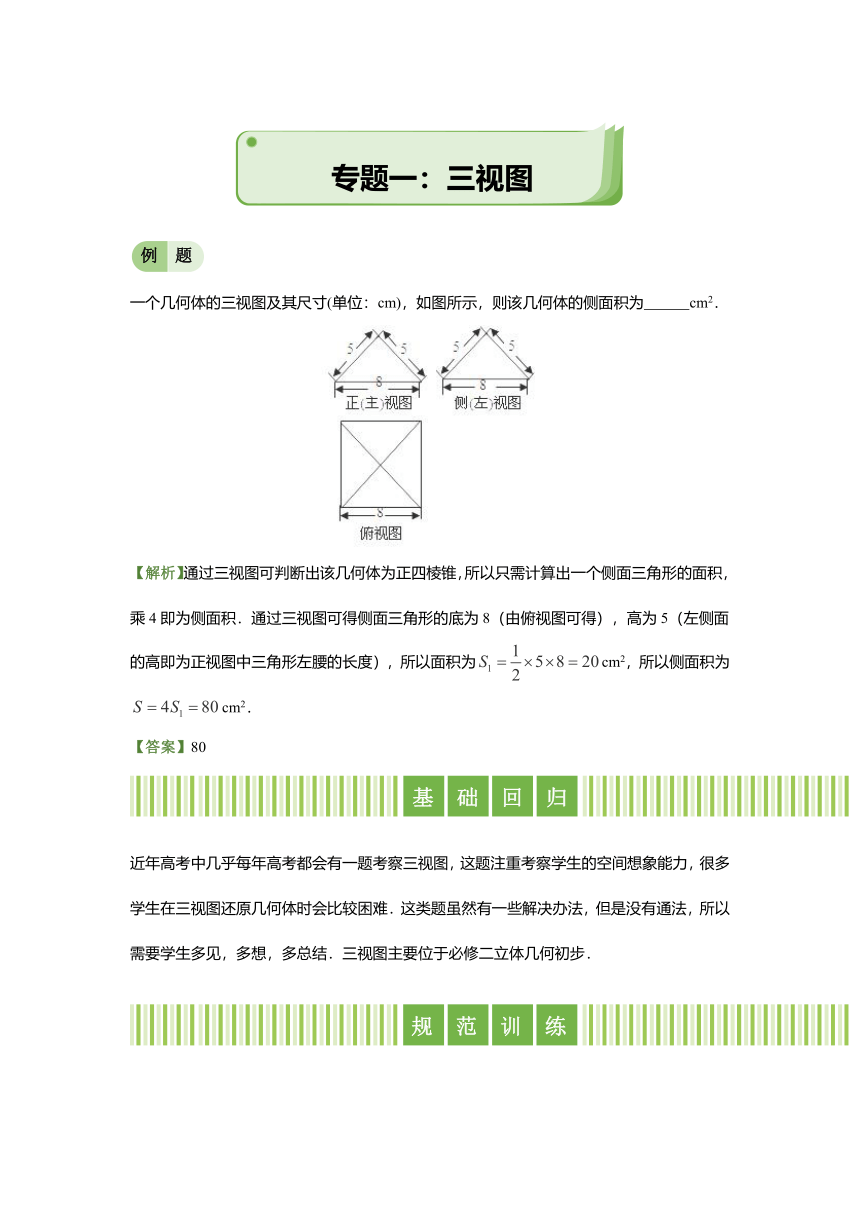
一个几何体的三视图及其尺寸(单位:cm),如图所示,则该几何体的侧面积为
cm2.
【解析】通过三视图可判断出该几何体为正四棱锥,所以只需计算出一个侧面三角形的面积,乘4即为侧面积.通过三视图可得侧面三角形的底为8(由俯视图可得),高为5(左侧面的高即为正视图中三角形左腰的长度),所以面积为cm2,所以侧面积为cm2.
【答案】80
近年高考中几乎每年高考都会有一题考察三视图,这题注重考察学生的空间想象能力,很多学生在三视图还原几何体时会比较困难.这类题虽然有一些解决办法,但是没有通法,所以需要学生多见,多想,多总结.三视图主要位于必修二立体几何初步.
一、选择题(20分/16min)
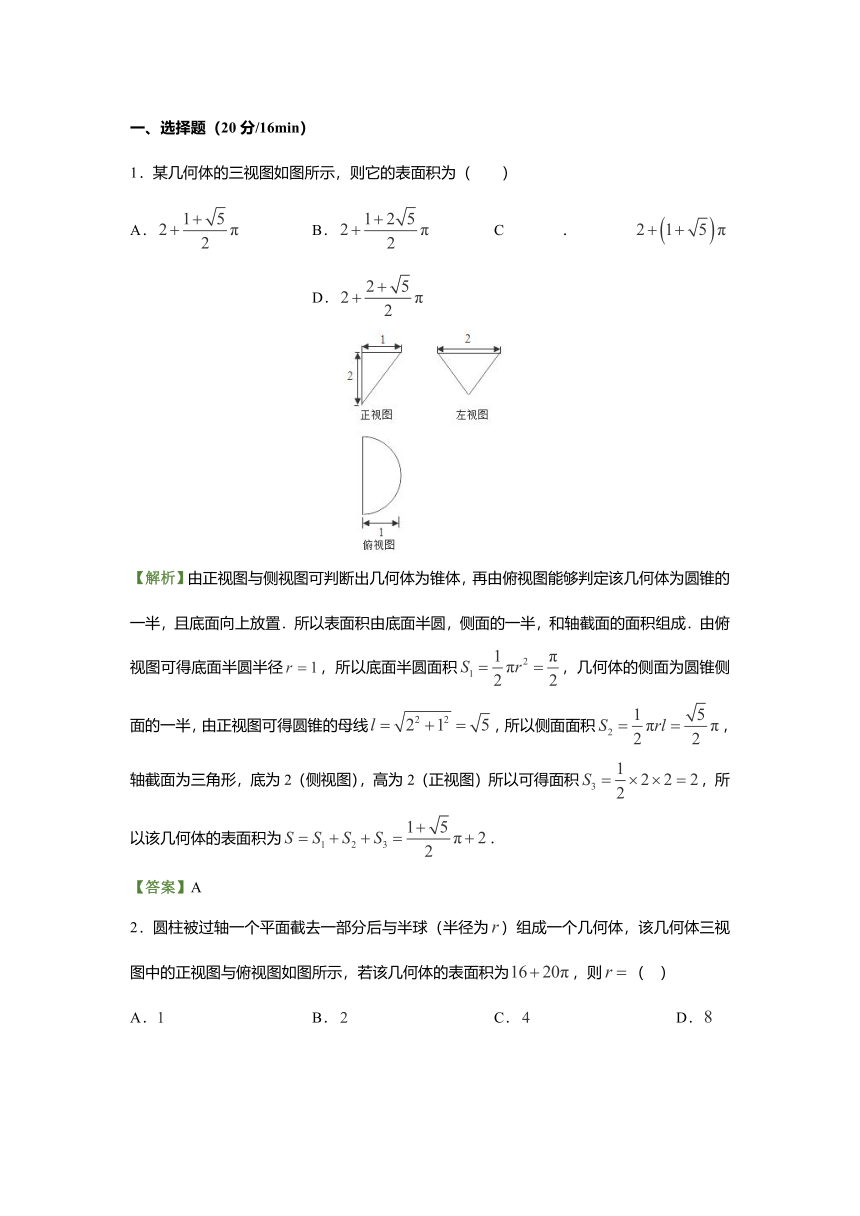
1.某几何体的三视图如图所示,则它的表面积为(
)
A.
B.
C.
D.
【解析】由正视图与侧视图可判断出几何体为锥体,再由俯视图能够判定该几何体为圆锥的一半,且底面向上放置.所以表面积由底面半圆,侧面的一半,和轴截面的面积组成.由俯视图可得底面半圆半径,所以底面半圆面积,几何体的侧面为圆锥侧面的一半,由正视图可得圆锥的母线,所以侧面面积,轴截面为三角形,底为2(侧视图),高为2(正视图)所以可得面积,所以该几何体的表面积为.
【答案】A
2.圆柱被过轴一个平面截去一部分后与半球(半径为)组成一个几何体,该几何体三视图中的正视图与俯视图如图所示,若该几何体的表面积为,则(
)
A.
B.
C.
D.
【解析】总体想法是用表示出几何体的表面积,在结合已知列出方程求解.由条件可知该几何体的表面积由一个半球,圆柱的半个底面,半球截面的一半(半圆),圆柱的半个侧面和圆柱的轴截面的面积组成.半球的面积为,半球截面的一半,圆柱半个底面面积为,圆柱半个侧面面积为,轴截面为矩形,底为,高为,所以面积为.进而表面积,所以,可解得.
【答案】B
3.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为(
)
A.4
B.2
C.6
D.8
【解析】由于长方体被平面所截,所以很难直接求出几何体的体积,可以考虑沿着截面再接上一个一模一样的几何体,从而拼成了一个长方体,因为长方体由两个完全一样的几何体拼成,所以所求体积为长方体体积的一半.从图上可得长方体的底面为正方形,且边长为,长方体的高为,所以,所以.
【答案】D
4.如图,网格纸上的小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为(
)
A.
B.
C.
D.
【解析】本题很难直接看出棱锥的底面积与高,但通过观察可看出此棱锥可能由正方体(棱长为2)通过切割而成,所以先画出正方体,再根据三视图中的实线虚线判断如何切割,正视图中可看出正方体用前后面的对角线所在平面将下方完全切掉,从左视图可看出正方体的右侧面(虚线)有切痕,俯视图体现出正方体的上底面有切痕.进而可得所求棱锥为一个四棱锥,底面是矩形,宽,长,因为平面,所以平面平面,过作的垂线,则有平面,即高,所以棱锥的体积为.
【答案】A
二、填空题(30分/24min)
5.已知某几何体的三视图如图所示,则该几何体的表面积等于________.
【解析】可初步判断出该几何体可由正方体截得一部分而构成.从三视图中可得去掉的一角为侧棱长为1,且两两垂直的三棱锥(如图所示),可得为边长是的等边三角形.所以,其余的面中有三个面是正方形的面积减去一个边长为1的等腰直角三角形的面积,即,另外三个面为完整的正方形,即,所以表面积.
【答案】
6.已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为
.
【解析】观察可发现这个棱锥是将一个侧面摆在地面上,而棱锥的真正底面体现在正视图(梯形)中,所以,而棱锥的高为侧视图的左右间距,即,所以.
【答案】
7.若某几何体的三视图如图所示,则此几何体的体积是________.
【解析】该几何体可拆为两个四棱柱,这两个四棱柱的高均为4(俯视图得到),其中一个四棱柱底面为正方形,边长为2(正视图得到),所以,另一个四棱柱底面为梯形,上下底分别为,所以,.故几何体的体积为.
【答案】
8.某几何体三视图如图所示(正方形边长为),则该几何体的体积为
.
【解析】由正视图与侧视图可得该几何体的轮廓为一个棱柱,从俯视图中可确定该组合体为正方体截掉了两部分,且这两部分刚好都是个圆柱,可拼成个圆柱.所以先计算出正方体的体积,而圆柱的底面半径为,高为,所以,所以组合体的体积为.
【答案】
9.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的表面积为________.
【解析】由正视图和侧视图可判断出几何体为锥体,结合俯视图可得该几何体为圆锥的一部分.其表面积由底面扇形,圆锥侧面的一部分和两个三角形截面组成,首先通过正视图线段的长度可得扇形的圆心角为,所以扇形面积,由侧视图可得圆锥的母线长,由底面扇形所占底面圆形的可得圆锥部分侧面面积也是圆锥侧面面积的,即,由正视图可得两个三角形的底为2,高为4,所以三角形面积为,所以几何体的表面积为.
【答案】
10.一个多面体的三视图如图所示,则该多面体的表面积为___________.
【解析】三视图可知该几何体为四棱锥,且顶点在底面的投影为底边的中点,可尝试作出四棱锥的直观图.底面为边长为2的正方形,所以面积,的底为2,高为(正视图的左侧直角边),所以.的底为2,高为2(侧视图的左右边),所以,的底为2,高,所以,所以棱锥的表面积.
【答案】
0
专题一:三视图
例
题
基础回归
规范训练
满分规范
1.时间:你是否在限定时间内完成?
□是
□否
2.教材:教材知识是否全面掌握?
□是
□否
满分规范
1.时间:你是否在限定时间内完成?
□是
□否
2.语言:答题学科用语是否精准规范?□是
□否
3.书写:字迹是否工整?卷面是否整洁?□是
□否
4.得分点:答题得分点是否全面无误?□是
□否
5.教材:教材知识是否全面掌握?
□是
□否
cm2.
【解析】通过三视图可判断出该几何体为正四棱锥,所以只需计算出一个侧面三角形的面积,乘4即为侧面积.通过三视图可得侧面三角形的底为8(由俯视图可得),高为5(左侧面的高即为正视图中三角形左腰的长度),所以面积为cm2,所以侧面积为cm2.
【答案】80
近年高考中几乎每年高考都会有一题考察三视图,这题注重考察学生的空间想象能力,很多学生在三视图还原几何体时会比较困难.这类题虽然有一些解决办法,但是没有通法,所以需要学生多见,多想,多总结.三视图主要位于必修二立体几何初步.
一、选择题(20分/16min)
1.某几何体的三视图如图所示,则它的表面积为(
)
A.
B.
C.
D.
【解析】由正视图与侧视图可判断出几何体为锥体,再由俯视图能够判定该几何体为圆锥的一半,且底面向上放置.所以表面积由底面半圆,侧面的一半,和轴截面的面积组成.由俯视图可得底面半圆半径,所以底面半圆面积,几何体的侧面为圆锥侧面的一半,由正视图可得圆锥的母线,所以侧面面积,轴截面为三角形,底为2(侧视图),高为2(正视图)所以可得面积,所以该几何体的表面积为.
【答案】A
2.圆柱被过轴一个平面截去一部分后与半球(半径为)组成一个几何体,该几何体三视图中的正视图与俯视图如图所示,若该几何体的表面积为,则(
)
A.
B.
C.
D.
【解析】总体想法是用表示出几何体的表面积,在结合已知列出方程求解.由条件可知该几何体的表面积由一个半球,圆柱的半个底面,半球截面的一半(半圆),圆柱的半个侧面和圆柱的轴截面的面积组成.半球的面积为,半球截面的一半,圆柱半个底面面积为,圆柱半个侧面面积为,轴截面为矩形,底为,高为,所以面积为.进而表面积,所以,可解得.
【答案】B
3.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为(
)
A.4
B.2
C.6
D.8
【解析】由于长方体被平面所截,所以很难直接求出几何体的体积,可以考虑沿着截面再接上一个一模一样的几何体,从而拼成了一个长方体,因为长方体由两个完全一样的几何体拼成,所以所求体积为长方体体积的一半.从图上可得长方体的底面为正方形,且边长为,长方体的高为,所以,所以.
【答案】D
4.如图,网格纸上的小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的体积为(
)
A.
B.
C.
D.
【解析】本题很难直接看出棱锥的底面积与高,但通过观察可看出此棱锥可能由正方体(棱长为2)通过切割而成,所以先画出正方体,再根据三视图中的实线虚线判断如何切割,正视图中可看出正方体用前后面的对角线所在平面将下方完全切掉,从左视图可看出正方体的右侧面(虚线)有切痕,俯视图体现出正方体的上底面有切痕.进而可得所求棱锥为一个四棱锥,底面是矩形,宽,长,因为平面,所以平面平面,过作的垂线,则有平面,即高,所以棱锥的体积为.
【答案】A
二、填空题(30分/24min)
5.已知某几何体的三视图如图所示,则该几何体的表面积等于________.
【解析】可初步判断出该几何体可由正方体截得一部分而构成.从三视图中可得去掉的一角为侧棱长为1,且两两垂直的三棱锥(如图所示),可得为边长是的等边三角形.所以,其余的面中有三个面是正方形的面积减去一个边长为1的等腰直角三角形的面积,即,另外三个面为完整的正方形,即,所以表面积.
【答案】
6.已知一棱锥的三视图如图所示,其中侧视图和俯视图都是等腰直角三角形,正视图为直角梯形,则该棱锥的体积为
.
【解析】观察可发现这个棱锥是将一个侧面摆在地面上,而棱锥的真正底面体现在正视图(梯形)中,所以,而棱锥的高为侧视图的左右间距,即,所以.
【答案】
7.若某几何体的三视图如图所示,则此几何体的体积是________.
【解析】该几何体可拆为两个四棱柱,这两个四棱柱的高均为4(俯视图得到),其中一个四棱柱底面为正方形,边长为2(正视图得到),所以,另一个四棱柱底面为梯形,上下底分别为,所以,.故几何体的体积为.
【答案】
8.某几何体三视图如图所示(正方形边长为),则该几何体的体积为
.
【解析】由正视图与侧视图可得该几何体的轮廓为一个棱柱,从俯视图中可确定该组合体为正方体截掉了两部分,且这两部分刚好都是个圆柱,可拼成个圆柱.所以先计算出正方体的体积,而圆柱的底面半径为,高为,所以,所以组合体的体积为.
【答案】
9.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的表面积为________.
【解析】由正视图和侧视图可判断出几何体为锥体,结合俯视图可得该几何体为圆锥的一部分.其表面积由底面扇形,圆锥侧面的一部分和两个三角形截面组成,首先通过正视图线段的长度可得扇形的圆心角为,所以扇形面积,由侧视图可得圆锥的母线长,由底面扇形所占底面圆形的可得圆锥部分侧面面积也是圆锥侧面面积的,即,由正视图可得两个三角形的底为2,高为4,所以三角形面积为,所以几何体的表面积为.
【答案】
10.一个多面体的三视图如图所示,则该多面体的表面积为___________.
【解析】三视图可知该几何体为四棱锥,且顶点在底面的投影为底边的中点,可尝试作出四棱锥的直观图.底面为边长为2的正方形,所以面积,的底为2,高为(正视图的左侧直角边),所以.的底为2,高为2(侧视图的左右边),所以,的底为2,高,所以,所以棱锥的表面积.
【答案】
0
专题一:三视图
例
题
基础回归
规范训练
满分规范
1.时间:你是否在限定时间内完成?
□是
□否
2.教材:教材知识是否全面掌握?
□是
□否
满分规范
1.时间:你是否在限定时间内完成?
□是
□否
2.语言:答题学科用语是否精准规范?□是
□否
3.书写:字迹是否工整?卷面是否整洁?□是
□否
4.得分点:答题得分点是否全面无误?□是
□否
5.教材:教材知识是否全面掌握?
□是
□否
同课章节目录
