2017年秋九年级数学上册第二十二章二次函数复习课件(新版)新人教版
文档属性
| 名称 | 2017年秋九年级数学上册第二十二章二次函数复习课件(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 389.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-25 20:59:46 | ||
图片预览





文档简介
课件29张PPT。第二十二章 二次函数九年级数学上(RJ)
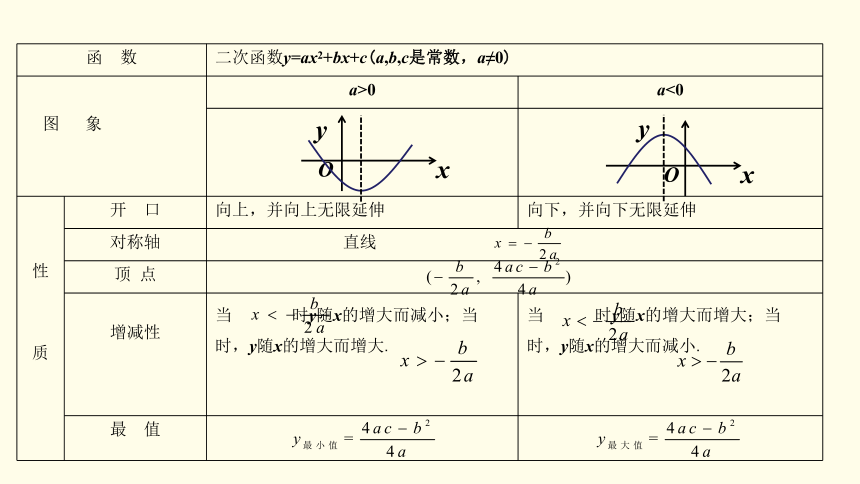
教学课件复习课知识网络专题复习 课堂小结课后训练二次函数二次函数的概念定义一般形式y=ax2+bx+c
(a,b,c是常数,a≠0)自变量的取值范围全体实数图 象一条抛物线解析式形式一般式y=ax2+bx+c(a≠0)顶点式y=a(x-h)2+k交点式y=a(x-x1)(x-x2)y=ax2+bx+c
(a≠0)性质六点、一轴、一方及增减性与最值二次函数与一元二次方程的关系抛物线与x轴交点的横坐标就是其对应一元二次方程的根二次函数的应用知识网络解析: (1)根据定义可知m2+5m+8=2且m+2≠0;
(2)在(1)的基础上根据a的符号再作确定;
(3)判断抛物线的增减性要结合开口方向及对称轴.专题复习解:(1)由题意得 解得∴满足条件的m=-3,这时二次函数的解析式为y=-x2+3.(2)抛物线y=-x2+3有最高点,该二次函数有最大值,最大值是3.(3)当x>0时,y随x的增大而减小.配套训练 1.抛物线y=(x-2)2+2的顶点坐标是( )
A.(-2,2) B. (2,-2) C. (2,2) D. (-2,-2)
2.已知二次函数y=x2-x+c的顶点在x轴上,则c= .
3.二次函数y=x2+bx+3 的对称轴是直线x=2 ,则 b=_______.C-4yy例2 抛物线y=ax2+bx+c (a≠0)与x轴的公共点是(-1,0),
(3,0),则这条抛物线的对称轴为_________.直线x=1 配套训练 1.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则①抛物线的对称轴是 ;
②当y<5时,x的取值范围是 .
③在此抛物线上有两点A(3,y1),B(4.5,y2),试比较y1和y2的大小:y1________y2(填“>”“<”或“=”).直线x=200时,x的取值范围是 .y-1(1) y2图象的顶点坐标 .
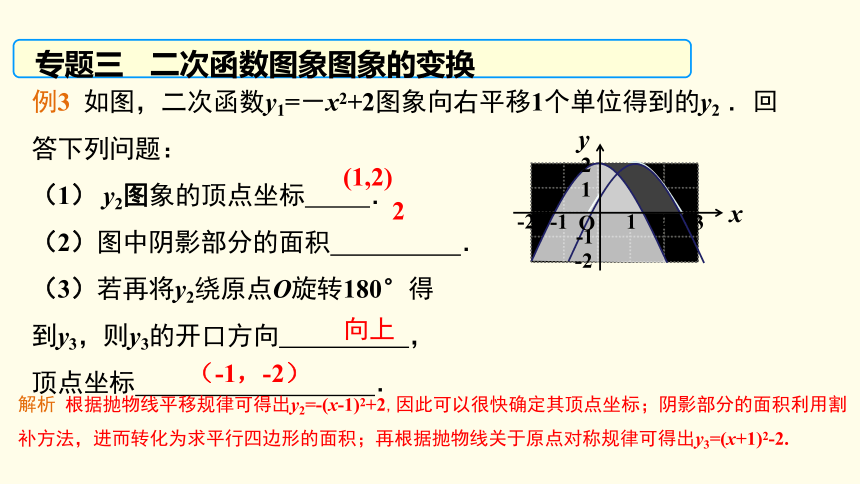
(2)图中阴影部分的面积 .
(3)若再将y2绕原点O旋转180°得
到y3,则y3的开口方向 ,
顶点坐标 .解析 根据抛物线平移规律可得出y2=-(x-1)2+2,因此可以很快确定其顶点坐标;阴影部分的面积利用割补方法,进而转化为求平行四边形的面积;再根据抛物线关于原点对称规律可得出y3=(x+1)2-2.(1,2)2向上(-1,-2)知识点复习 抛物线y=a(x-h)2+k的平移规律:左右平移,括号内左加右减;上下平移,括号外上加下减.配套训练 要得到抛物线y=2(x-4)2-1,可以将抛物线y=2x2 ( )
A.向左平移4个单位长度,再向上平移1个单位长度
B.向左平移4个单位长度,再向下平移1个单位长度
C.向右平移4个单位长度,再向上平移1个单位长度
D.向右平移4个单位长度,再向下平移1个单位长度B例4 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为
(-1,0).则下面的四个结论 :①2a+b=0;②4a-2b+c>0;③abc>0;④当y<0时,x<-1或x>3.其中正确的是( )
A.①② B. ①③
C.①④ D. ②③ C知识点复习 抛物线y=ax2+bx+c中的符号问题:
① a的符号决定开口方向;
② a、b的符号共同决定对称轴的位置,“左同右异”;
③ c的符号决定抛物线与y轴的交点位置.配套训练 1.已知二次函数y=ax2+bx+c(a ≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:
①b2-4ac>0; ②abc<0; ③m>2.其中正确结论的个数是( )
A.0 B.1 C. 2 D. 3D配套训练 2.如图,函数y=ax2-2x+1和y=ax+a(a是常数,且a ≠0)在同一平面直角坐标系的图象可能是( )A例5 结合二次函数y=ax2+bx+c图象,解答下列问题:
①写出方程ax2+bx+c=0的根;
②写出不等式ax2+bx+c>0的解集;
③写出y随x的增大而减小的自变量x的取值范围;
④若方程ax2+bx+c=k有两个不相等的实数根,
求k的取值范围.解析 本题结合图象从中发现信息进行解题.解:(1)由图象可知,函数y=ax2+bx+c的图象与x轴相交于(-1,0),(3,0)两点.∴方程的根为x1=-1,x2=3;(2)由图象可知当-11;(4)要使得有ax2+bx+c=k两个不相等的实数根,即直线x=k与二次函数图象有两个交点,∴k的取值范围为k<5.配套训练 已知抛物线y=ax2+bx+c的图象如图所示,则关于x的方程 ax2+bx+c-8=0的根的情况是( )
A.有两个不相等的正实数根
B.有两个异号实数根
C.有两个相等的实数根
D.没有实数根C 例6 你能求出图中抛物线的解析式吗?解析 图象中提供了我们解题的很多信息,如可知道抛物线与x轴的两个交点坐标是(-1,0)和(3,0),还可以知道对称轴是直线x=2及顶点坐标是(1,4).你有几种方法可以求这条抛物线的解析式,你最喜欢哪一种?解:设抛物线的解析式为y=a(x-h)2+k.
由图象可知抛物线的对称轴为直线x=1,与x轴相交于点(-1,0),(3,0),顶点坐标为(1,4),
∴有y=a(x-1)2+4,
代入(-1,0).∴a(-1-1)2+4=0,∴a=-1,
∴抛物线的解析式为y=-(x-1)2+4.方法提示 知道顶点坐标,通常设顶点式y=a(x-h)2+k;知道抛物线与x轴的两个交点坐标,通常设交点式y=a(x-x1)(x-x2);知道抛物线上的三点坐标,可选用一般式y=ax2+bx+c,三种情况都可以时选用最熟悉的方法.配套训练 已知二次函数当x=1时,有最大值-6,且其图象过点(2,-8),则二次函数的解析式是 .y=-2(x-1)2-6例7 跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距为4米,距地面均为1米,丙、丁同学分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处,刚好通过他们的头顶,已知丙同学的身高是1.5米.
(1)请你算一算丁同学的身高.(0,1)(4,1)(1,1.5)解得: ,所以抛物线解析式为
当x=2.5时,y=1.625.所以丁同学的身高为1.625米.
解:如图建立平面直角坐标系,可设抛物线的解析式为y=ax2+bx+1
点(1,1.5)、(4,1)在抛物线上,得
xO y(0,1)(4,1)(1,1.5)
(2)如果身高为1.5米的丙同学站在甲、乙同学之间,且离甲同学的距离为s米, 要使绳子甩到最高处时超过他的头顶,请结合图像,直接写出s的取值范围.1A.开口向下,顶点坐标(5,3) B.开口向上,顶点坐标(5,3)
C.开口向下,顶点坐标(-5,3) D.开口向上,顶点坐标(-5,3)
A2.当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是
( )A课后训练3.将二次函数y=2x2-1的图象沿y轴向上平移2个单位,所得到的图象的函数解析式是 .y=2x2+14.二次函数y=ax2+bx+c的图象经过点(3,6)和(-1,6),则对称轴为 .直线x=15.如图1,抛物线y=ax2+bx+c与x轴交于点A(1,0)、B(-3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
y=-x2-2x+3Q(-1,2)解:(1)由题设,将A(1,0)、B(-3,0)、C(0,3)代入y=ax2+bx+c,∴抛物线的解析式为y=-x2-2x+3;(2)存在,理由如下:作点C关于抛物线对称轴直线x=-1的对称点C’,由抛物线的性质可知点C‘在抛物线上,点C’的坐标是(-2,3),连接点C’A交抛物线的对称轴直线x=-1与点Q,点Q即为所求.设直线C‘A的解析式为y=kx+m,代入(-2,3)和(0,1)可得k=-1,m=1.所以Q的坐标为(-1,2);
教学课件复习课知识网络专题复习 课堂小结课后训练二次函数二次函数的概念定义一般形式y=ax2+bx+c
(a,b,c是常数,a≠0)自变量的取值范围全体实数图 象一条抛物线解析式形式一般式y=ax2+bx+c(a≠0)顶点式y=a(x-h)2+k交点式y=a(x-x1)(x-x2)y=ax2+bx+c
(a≠0)性质六点、一轴、一方及增减性与最值二次函数与一元二次方程的关系抛物线与x轴交点的横坐标就是其对应一元二次方程的根二次函数的应用知识网络解析: (1)根据定义可知m2+5m+8=2且m+2≠0;
(2)在(1)的基础上根据a的符号再作确定;
(3)判断抛物线的增减性要结合开口方向及对称轴.专题复习解:(1)由题意得 解得∴满足条件的m=-3,这时二次函数的解析式为y=-x2+3.(2)抛物线y=-x2+3有最高点,该二次函数有最大值,最大值是3.(3)当x>0时,y随x的增大而减小.配套训练 1.抛物线y=(x-2)2+2的顶点坐标是( )
A.(-2,2) B. (2,-2) C. (2,2) D. (-2,-2)
2.已知二次函数y=x2-x+c的顶点在x轴上,则c= .
3.二次函数y=x2+bx+3 的对称轴是直线x=2 ,则 b=_______.C-4yy例2 抛物线y=ax2+bx+c (a≠0)与x轴的公共点是(-1,0),
(3,0),则这条抛物线的对称轴为_________.直线x=1 配套训练 1.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:则①抛物线的对称轴是 ;
②当y<5时,x的取值范围是 .
③在此抛物线上有两点A(3,y1),B(4.5,y2),试比较y1和y2的大小:y1________y2(填“>”“<”或“=”).直线x=20
(2)图中阴影部分的面积 .
(3)若再将y2绕原点O旋转180°得
到y3,则y3的开口方向 ,
顶点坐标 .解析 根据抛物线平移规律可得出y2=-(x-1)2+2,因此可以很快确定其顶点坐标;阴影部分的面积利用割补方法,进而转化为求平行四边形的面积;再根据抛物线关于原点对称规律可得出y3=(x+1)2-2.(1,2)2向上(-1,-2)知识点复习 抛物线y=a(x-h)2+k的平移规律:左右平移,括号内左加右减;上下平移,括号外上加下减.配套训练 要得到抛物线y=2(x-4)2-1,可以将抛物线y=2x2 ( )
A.向左平移4个单位长度,再向上平移1个单位长度
B.向左平移4个单位长度,再向下平移1个单位长度
C.向右平移4个单位长度,再向上平移1个单位长度
D.向右平移4个单位长度,再向下平移1个单位长度B例4 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为直线x=1,点B坐标为
(-1,0).则下面的四个结论 :①2a+b=0;②4a-2b+c>0;③abc>0;④当y<0时,x<-1或x>3.其中正确的是( )
A.①② B. ①③
C.①④ D. ②③ C知识点复习 抛物线y=ax2+bx+c中的符号问题:
① a的符号决定开口方向;
② a、b的符号共同决定对称轴的位置,“左同右异”;
③ c的符号决定抛物线与y轴的交点位置.配套训练 1.已知二次函数y=ax2+bx+c(a ≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,有下列结论:
①b2-4ac>0; ②abc<0; ③m>2.其中正确结论的个数是( )
A.0 B.1 C. 2 D. 3D配套训练 2.如图,函数y=ax2-2x+1和y=ax+a(a是常数,且a ≠0)在同一平面直角坐标系的图象可能是( )A例5 结合二次函数y=ax2+bx+c图象,解答下列问题:
①写出方程ax2+bx+c=0的根;
②写出不等式ax2+bx+c>0的解集;
③写出y随x的增大而减小的自变量x的取值范围;
④若方程ax2+bx+c=k有两个不相等的实数根,
求k的取值范围.解析 本题结合图象从中发现信息进行解题.解:(1)由图象可知,函数y=ax2+bx+c的图象与x轴相交于(-1,0),(3,0)两点.∴方程的根为x1=-1,x2=3;(2)由图象可知当-1
A.有两个不相等的正实数根
B.有两个异号实数根
C.有两个相等的实数根
D.没有实数根C 例6 你能求出图中抛物线的解析式吗?解析 图象中提供了我们解题的很多信息,如可知道抛物线与x轴的两个交点坐标是(-1,0)和(3,0),还可以知道对称轴是直线x=2及顶点坐标是(1,4).你有几种方法可以求这条抛物线的解析式,你最喜欢哪一种?解:设抛物线的解析式为y=a(x-h)2+k.
由图象可知抛物线的对称轴为直线x=1,与x轴相交于点(-1,0),(3,0),顶点坐标为(1,4),
∴有y=a(x-1)2+4,
代入(-1,0).∴a(-1-1)2+4=0,∴a=-1,
∴抛物线的解析式为y=-(x-1)2+4.方法提示 知道顶点坐标,通常设顶点式y=a(x-h)2+k;知道抛物线与x轴的两个交点坐标,通常设交点式y=a(x-x1)(x-x2);知道抛物线上的三点坐标,可选用一般式y=ax2+bx+c,三种情况都可以时选用最熟悉的方法.配套训练 已知二次函数当x=1时,有最大值-6,且其图象过点(2,-8),则二次函数的解析式是 .y=-2(x-1)2-6例7 跳绳时,绳甩到最高处的形状可近似的看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距为4米,距地面均为1米,丙、丁同学分别站在距甲拿绳的手水平距离1米、2.5米处,绳子甩到最高处,刚好通过他们的头顶,已知丙同学的身高是1.5米.
(1)请你算一算丁同学的身高.(0,1)(4,1)(1,1.5)解得: ,所以抛物线解析式为
当x=2.5时,y=1.625.所以丁同学的身高为1.625米.
解:如图建立平面直角坐标系,可设抛物线的解析式为y=ax2+bx+1
点(1,1.5)、(4,1)在抛物线上,得
xO y(0,1)(4,1)(1,1.5)
(2)如果身高为1.5米的丙同学站在甲、乙同学之间,且离甲同学的距离为s米, 要使绳子甩到最高处时超过他的头顶,请结合图像,直接写出s的取值范围.1
C.开口向下,顶点坐标(-5,3) D.开口向上,顶点坐标(-5,3)
A2.当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax2+bx+c的是
( )A课后训练3.将二次函数y=2x2-1的图象沿y轴向上平移2个单位,所得到的图象的函数解析式是 .y=2x2+14.二次函数y=ax2+bx+c的图象经过点(3,6)和(-1,6),则对称轴为 .直线x=15.如图1,抛物线y=ax2+bx+c与x轴交于点A(1,0)、B(-3,0)两点,与y轴交于点C(0,3).
(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出点Q的坐标;若不存在,请说明理由.
y=-x2-2x+3Q(-1,2)解:(1)由题设,将A(1,0)、B(-3,0)、C(0,3)代入y=ax2+bx+c,∴抛物线的解析式为y=-x2-2x+3;(2)存在,理由如下:作点C关于抛物线对称轴直线x=-1的对称点C’,由抛物线的性质可知点C‘在抛物线上,点C’的坐标是(-2,3),连接点C’A交抛物线的对称轴直线x=-1与点Q,点Q即为所求.设直线C‘A的解析式为y=kx+m,代入(-2,3)和(0,1)可得k=-1,m=1.所以Q的坐标为(-1,2);
同课章节目录
