七年级数学下册7平面图形的认识(二)综合卷(新版)苏科版
文档属性
| 名称 | 七年级数学下册7平面图形的认识(二)综合卷(新版)苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 191.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-26 08:38:34 | ||
图片预览


文档简介
第7章
平面图形的认识(二)
一、选择题。(每题3分,共21分)
l.如图,△DEF经过怎样的平移得到△ABC
(
)
A.把△DEF向左平移4个单位,再向下平移2个单位
B.把△DEF向右平移4个单位,再向下平移2个单位
C.把△DEF向右平移4个单位,再向上平移2个单位
D.把△DEF向左平移4个单位,再向上平移2个单位
2.如图,直线a、b被直线c所截,下列说法正确的是
(
)
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90
D.当∠1+∠2=180 时,一定有a∥b
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么这两次拐弯的角度可能是
(
)
A.先向左转130 ,再向左转50
B.先向左转50 ,再向右转50
C.先向左转50 ,再向右转40
D.先向左转50 ,再向左转40
4.现有3
cm、4
cm、7
cm、9
cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是
(
)
A.1个
B.2个
C.3个
D.4个
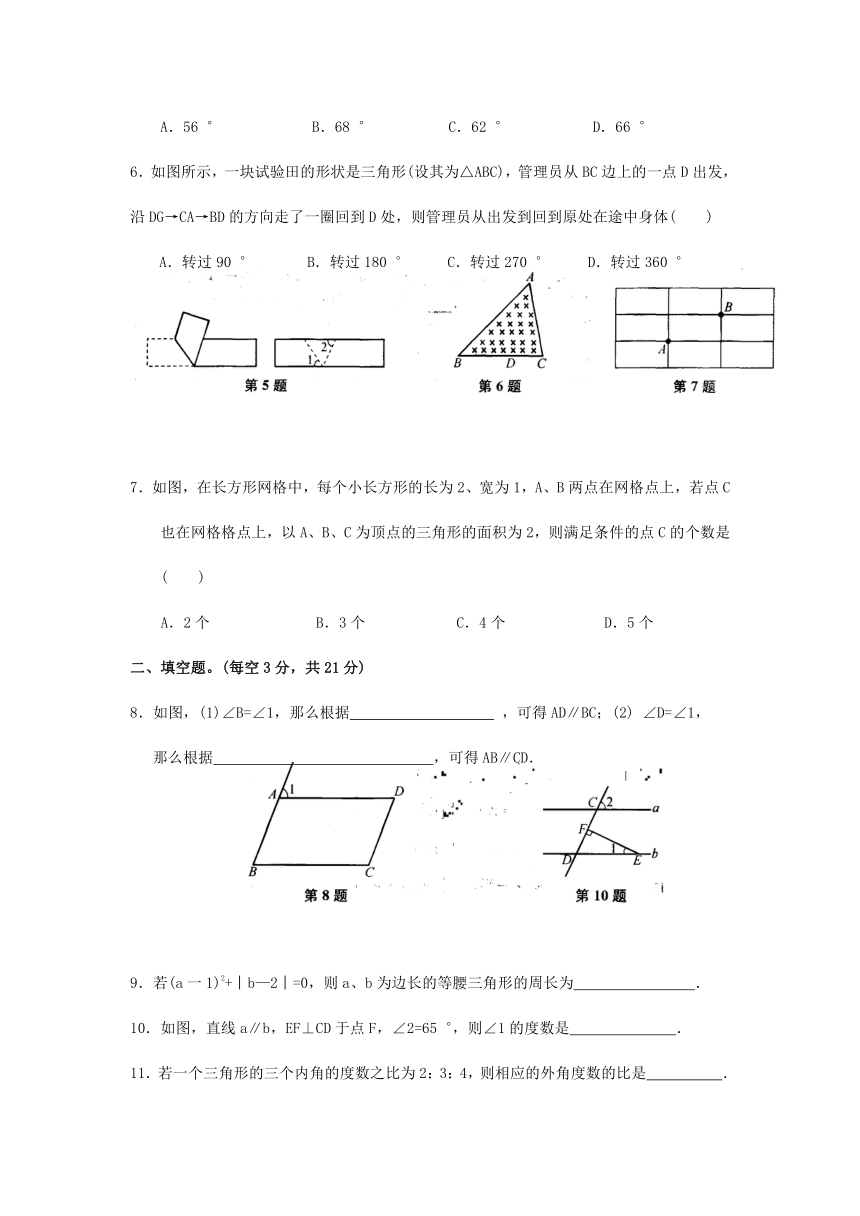
5.将一张长方形纸片如图所示折叠后,再展开,如果∠1=56 ,那么∠2等于
(
)
A.56
B.68
C.62
D.66
6.如图所示,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DG→CA→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体(
)
A.转过90
B.转过180
C.转过270
D.转过360
7.如图,在长方形网格中,每个小长方形的长为2、宽为1,A、B两点在网格点上,若点C也在网格格点上,以A、B、C为顶点的三角形的面积为2,则满足条件的点C的个数是
(
)
A.2个
B.3个
C.4个
D.5个
二、填空题。(每空3分,共21分)
8.如图,(1)∠B=∠1,那么根据
,可得AD∥BC;(2)
∠D=∠1,
那么根据
,可得AB∥CD.
9.若(a一1)2+︱b—2︱=0,则a、b为边长的等腰三角形的周长为
.
10.如图,直线a∥b,EF⊥CD于点F,∠2=65 ,则∠1的度数是
.
11.若一个三角形的三个内角的度数之比为2:3:4,则相应的外角度数的比是
.
12.如图,将边长为3个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长为
.
13.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放
在一直线上),那图中∠a=
.
14.某机器零件的横截面积如图所示,按要求线段AB和DC的延长线相交成直角才算合格.
若一名工人测得∠A=23 ,∠D=31 ,∠AED=143 ,则该零件
(填“合格”或“不合格”).
三、解答题。(共58分)
15.(8分)如图,在△ABC中,∠BAC是钝角
(1)画出边BC上的中线AD;
(2)画出边BC上的高AH;
(3)在所画图形中,共有
个三角形,其中面积一定相等的三角形是
16.(8分)如图,在△ABC中,DE∥BC,∠DBE=30 ,∠EBC=25 .求∠BDE的度数.
17.(8分)若将一个多边形的边数减少一半,则它的内角和是1080 ,求原多边形的内角和.
18.(8分)如图,在△ABC中,已知∠A:
∠ABC:
∠ACB=3:4:5,BD、CE分别是边AC、
AB上的高,BD、CE相交于点H.求∠BHC的度数.
19.(8分)如图,在四边形ABCD中,∠A=∠C=90 ,BE平分∠ABC,DF平分∠ADC,BE与DF有何位置关系?试说明理由。
20.(8分)如图,∠1+∠2=180 ,∠B=∠3,你能判断∠ACB与∠AED之间的大小关系吗
请说明理由.
21.(10分)(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两
条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30 ,则ABC+
∠ACB=
,∠XBC+∠XCB=
;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边Xy、XZ仍
然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的人小是否变化 若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
参考答案
1.A
2.D
3.B
4.B
5.B
6.D
7.C
8.同位角相等,两直线平行内错角相等,两直线平行
9.5
10.25°
11.7:6:5
12.13
13.75°
14.不合格
15.(1),(2)作图略
(3)6个,△ABD,△ACD
16.∵∠DBF=30°,∠EBC=25°,∴∠DBC=∠DBE
+∠EBC=55°.∵DE∥BC,
∴∠DBC+BDE=180°.∴∠BDE=180°-∠DBC=125°.
17.设原多边形的边数为理.根据题意,得(一2)·180°=l
080°,解得,n=16.∴原多边形的内角和为(16-2)×180°=2
520°.
18.∵∠A:∠ABC:∠AGB=3:4:5,∠A+∠ABC+∠ACB=180°,∴∠=45°,∠ABC=60°,
∠ACB=75°.∵BD、CE是高,∴∠CEB=∠CDB
=90°.∴∠ECB=30°,
∠DBC=15°.∴∠BHC
=135°.
19.BE∥DF
理由:∵∠A=∠C
=90°,又∵四边形ABCD的内角和为(4-2)×180=360°,
∴∠ABC
+∠ADC=180°.∵BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CBE=∠ABC,∠ADF=∠CDF=∠ADC.∴∠ABE+∠ADF=
(∠ABC+∠ADC)=
×180°=90°.
∵∠ABE
+∠AEB=180°一∠A=90°,∴∠ADF=∠AEB,∴BE∥DF.
20.∠AED=∠ACB理由:∵∠1+∠2=180°,∠1+
∠EFD=180°∴∠2=∠EFD.∴BD∥FE.∴∠3
=∠ADE.∵∠3=∠B,∴∠B=∠ADE∴DE∥BC.∴∠AED=∠ACB.
21.解:(1)
∠ABC+∠ACB=180°-∠A=180°一30°=150°,
∠XBC+∠XCB=180°-∠X=180°-90°=90°
(2)不变化.
∵∠ABX+∠XBC+∠XCB+∠ACX+∠A
=180°,
又∠XBC+∠XBC=180°-∠X=180°-9O°=90°,
∴∠ABX+∠ACX=180°-90°-30°=60°.
平面图形的认识(二)
一、选择题。(每题3分,共21分)
l.如图,△DEF经过怎样的平移得到△ABC
(
)
A.把△DEF向左平移4个单位,再向下平移2个单位
B.把△DEF向右平移4个单位,再向下平移2个单位
C.把△DEF向右平移4个单位,再向上平移2个单位
D.把△DEF向左平移4个单位,再向上平移2个单位
2.如图,直线a、b被直线c所截,下列说法正确的是
(
)
A.当∠1=∠2时,一定有a∥b
B.当a∥b时,一定有∠1=∠2
C.当a∥b时,一定有∠1+∠2=90
D.当∠1+∠2=180 时,一定有a∥b
3.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么这两次拐弯的角度可能是
(
)
A.先向左转130 ,再向左转50
B.先向左转50 ,再向右转50
C.先向左转50 ,再向右转40
D.先向左转50 ,再向左转40
4.现有3
cm、4
cm、7
cm、9
cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是
(
)
A.1个
B.2个
C.3个
D.4个
5.将一张长方形纸片如图所示折叠后,再展开,如果∠1=56 ,那么∠2等于
(
)
A.56
B.68
C.62
D.66
6.如图所示,一块试验田的形状是三角形(设其为△ABC),管理员从BC边上的一点D出发,沿DG→CA→BD的方向走了一圈回到D处,则管理员从出发到回到原处在途中身体(
)
A.转过90
B.转过180
C.转过270
D.转过360
7.如图,在长方形网格中,每个小长方形的长为2、宽为1,A、B两点在网格点上,若点C也在网格格点上,以A、B、C为顶点的三角形的面积为2,则满足条件的点C的个数是
(
)
A.2个
B.3个
C.4个
D.5个
二、填空题。(每空3分,共21分)
8.如图,(1)∠B=∠1,那么根据
,可得AD∥BC;(2)
∠D=∠1,
那么根据
,可得AB∥CD.
9.若(a一1)2+︱b—2︱=0,则a、b为边长的等腰三角形的周长为
.
10.如图,直线a∥b,EF⊥CD于点F,∠2=65 ,则∠1的度数是
.
11.若一个三角形的三个内角的度数之比为2:3:4,则相应的外角度数的比是
.
12.如图,将边长为3个单位的等边△ABC沿边BC向右平移2个单位得到△DEF,则四边形ABFD的周长为
.
13.将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放
在一直线上),那图中∠a=
.
14.某机器零件的横截面积如图所示,按要求线段AB和DC的延长线相交成直角才算合格.
若一名工人测得∠A=23 ,∠D=31 ,∠AED=143 ,则该零件
(填“合格”或“不合格”).
三、解答题。(共58分)
15.(8分)如图,在△ABC中,∠BAC是钝角
(1)画出边BC上的中线AD;
(2)画出边BC上的高AH;
(3)在所画图形中,共有
个三角形,其中面积一定相等的三角形是
16.(8分)如图,在△ABC中,DE∥BC,∠DBE=30 ,∠EBC=25 .求∠BDE的度数.
17.(8分)若将一个多边形的边数减少一半,则它的内角和是1080 ,求原多边形的内角和.
18.(8分)如图,在△ABC中,已知∠A:
∠ABC:
∠ACB=3:4:5,BD、CE分别是边AC、
AB上的高,BD、CE相交于点H.求∠BHC的度数.
19.(8分)如图,在四边形ABCD中,∠A=∠C=90 ,BE平分∠ABC,DF平分∠ADC,BE与DF有何位置关系?试说明理由。
20.(8分)如图,∠1+∠2=180 ,∠B=∠3,你能判断∠ACB与∠AED之间的大小关系吗
请说明理由.
21.(10分)(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两
条直角边XY、XZ分别经过点B、C直角顶点X在△ABC内部,若∠A=30 ,则ABC+
∠ACB=
,∠XBC+∠XCB=
;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边Xy、XZ仍
然分别经过点B、C,直角顶点X还在△ABC内部,那么∠ABX+∠ACX的人小是否变化 若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
参考答案
1.A
2.D
3.B
4.B
5.B
6.D
7.C
8.同位角相等,两直线平行内错角相等,两直线平行
9.5
10.25°
11.7:6:5
12.13
13.75°
14.不合格
15.(1),(2)作图略
(3)6个,△ABD,△ACD
16.∵∠DBF=30°,∠EBC=25°,∴∠DBC=∠DBE
+∠EBC=55°.∵DE∥BC,
∴∠DBC+BDE=180°.∴∠BDE=180°-∠DBC=125°.
17.设原多边形的边数为理.根据题意,得(一2)·180°=l
080°,解得,n=16.∴原多边形的内角和为(16-2)×180°=2
520°.
18.∵∠A:∠ABC:∠AGB=3:4:5,∠A+∠ABC+∠ACB=180°,∴∠=45°,∠ABC=60°,
∠ACB=75°.∵BD、CE是高,∴∠CEB=∠CDB
=90°.∴∠ECB=30°,
∠DBC=15°.∴∠BHC
=135°.
19.BE∥DF
理由:∵∠A=∠C
=90°,又∵四边形ABCD的内角和为(4-2)×180=360°,
∴∠ABC
+∠ADC=180°.∵BE平分∠ABC,DF平分∠ADC,∴∠ABE=∠CBE=∠ABC,∠ADF=∠CDF=∠ADC.∴∠ABE+∠ADF=
(∠ABC+∠ADC)=
×180°=90°.
∵∠ABE
+∠AEB=180°一∠A=90°,∴∠ADF=∠AEB,∴BE∥DF.
20.∠AED=∠ACB理由:∵∠1+∠2=180°,∠1+
∠EFD=180°∴∠2=∠EFD.∴BD∥FE.∴∠3
=∠ADE.∵∠3=∠B,∴∠B=∠ADE∴DE∥BC.∴∠AED=∠ACB.
21.解:(1)
∠ABC+∠ACB=180°-∠A=180°一30°=150°,
∠XBC+∠XCB=180°-∠X=180°-90°=90°
(2)不变化.
∵∠ABX+∠XBC+∠XCB+∠ACX+∠A
=180°,
又∠XBC+∠XBC=180°-∠X=180°-9O°=90°,
∴∠ABX+∠ACX=180°-90°-30°=60°.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
