坐标系中计算三角形面积课件
图片预览





文档简介
课件17张PPT。湖北省郧阳区城关一中 熊勇坐标系中三角形面积的计算学习目标1.学会选择适当的方法计算平面直角坐标系中三角形的面积;
2.继续树立数形结合思想,进一步培养边做题边总结规律的好习惯 。坐标系中三角形面积的计算基础回顾1、直角坐标系中下列位置的点各有哪些特点?
(1)象限中的点 ; (2)坐标轴上的点;
(3) 平行于坐标轴的直线上的点.
2、点 M(- 2,3)到 x轴的距离是_____,
到 y轴的距离是____.
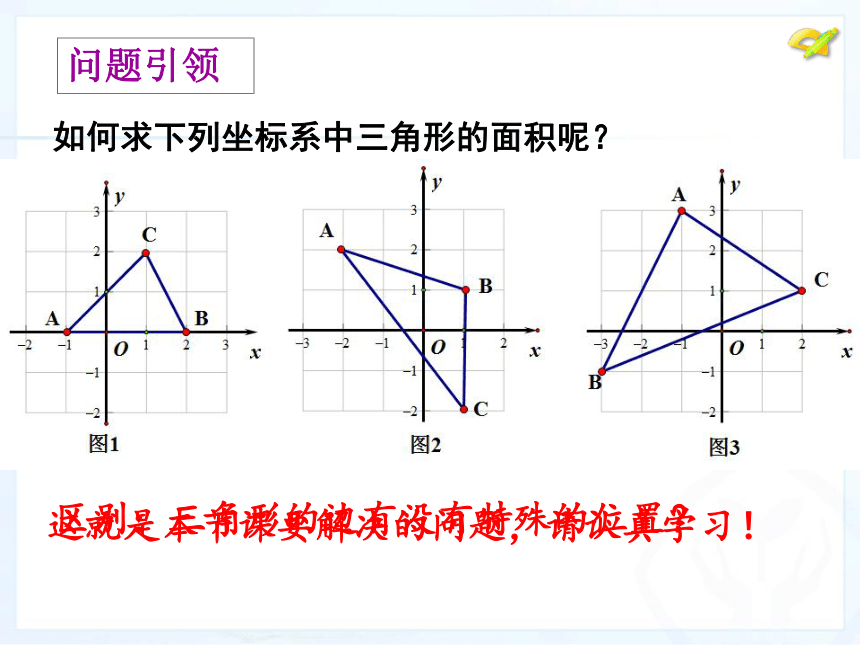
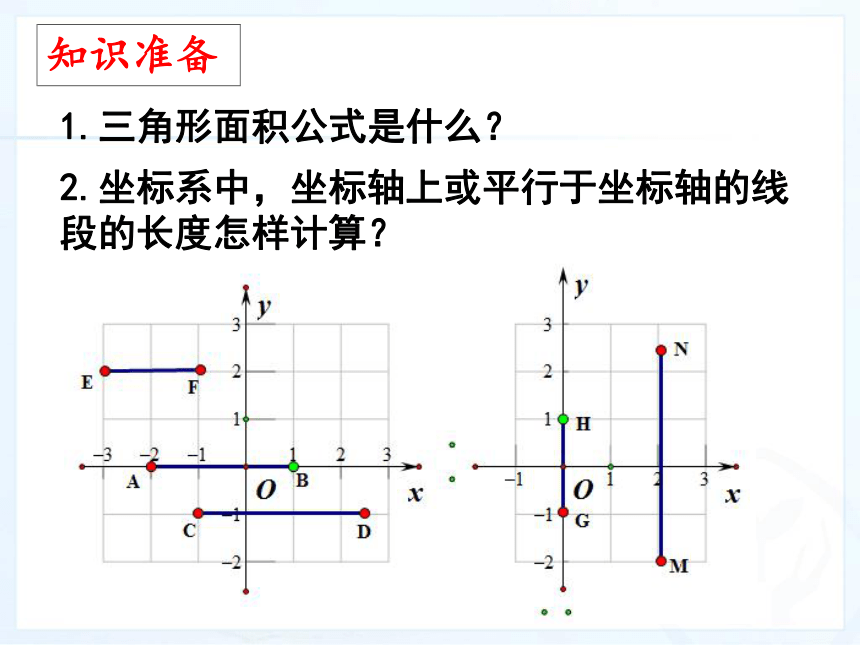
1.第一象限: 第二象限 : 第三象限: 第四象限: 2.x轴上点: y轴上点: 3.平行于x轴的直线上点: 平行于y轴的直线上点: 4.点到x轴的距离是 点到y轴的距离是记住规律(+,+)(-,+)(-,-)(+,-)纵坐标为0横坐标为0纵坐标相等横坐标相等纵坐标的绝对值横坐标的绝对值如何求下列坐标系中三角形的面积呢?问题引领这就是本节课要解决的问题,请认真学习!区别:三角形的边有没有特殊的位置?1.三角形面积公式是什么?2.坐标系中,坐标轴上或平行于坐标轴的线段的长度怎样计算?知识准备例1. 已知A(-1,0),B(2,0),C(1,2) 求S△ABC 思考:
如何选择底边?长度怎样计算?
高呢?长度是多少?自主探究例1.已知A(-1,0),B(2,0),C(1,2) 求S△ABC 解:过C作CD⊥x轴于D,
∵ C(1,2)
∴ CD=2
∵ A(-1,0),B(2,0)
∴ AB=3
∴ S△ABC=技巧:
选择坐标轴上的边为底边例2.已知A(-2,2),B(1,1),C(1,-2) 求S△ABC 思考:
如何选择底边?长度怎样计算?
如何作高?高长是多少?变式例题例2.已知A(-2,2),B(1,1),C(1,-2) 求S△ABC口述解题过程技巧:
选择与坐标轴平行的边为底边例3.已知A(-1,3),B(-3,-1),C(2,1) 求S△ABC 思考:
若按公式法,底边、高的长度容易计算吗?
该怎么办呢?合作探究要注意听讲哟!那个同学
若三角形三边与坐标轴都不平行时,将三角形补成一个边与坐标轴平行的长方形或梯形。
---割补法求面积例3.已知A(-1,3),B(-3,-1),C(2,1) 求S△ABC 在坐标系中求三角形面积时,要依据边的位置选择计算方法:
当至少有一边在坐标轴上或与坐标轴平行时,直接用公式法求面积,否则要利用图形割补法求面积。归纳总结本节课你学会了什么?还有什么困惑?温馨提示一、已知A(1,0), B(-1,2),点C在x轴上,△ABC的面积为3,
求C点坐标。应用拓展课后作业《全能学案》P56 第1--7题;二、收集与三角形面积相关的结论。同学们
:不断努力哟!
2.继续树立数形结合思想,进一步培养边做题边总结规律的好习惯 。坐标系中三角形面积的计算基础回顾1、直角坐标系中下列位置的点各有哪些特点?
(1)象限中的点 ; (2)坐标轴上的点;
(3) 平行于坐标轴的直线上的点.
2、点 M(- 2,3)到 x轴的距离是_____,
到 y轴的距离是____.
1.第一象限: 第二象限 : 第三象限: 第四象限: 2.x轴上点: y轴上点: 3.平行于x轴的直线上点: 平行于y轴的直线上点: 4.点到x轴的距离是 点到y轴的距离是记住规律(+,+)(-,+)(-,-)(+,-)纵坐标为0横坐标为0纵坐标相等横坐标相等纵坐标的绝对值横坐标的绝对值如何求下列坐标系中三角形的面积呢?问题引领这就是本节课要解决的问题,请认真学习!区别:三角形的边有没有特殊的位置?1.三角形面积公式是什么?2.坐标系中,坐标轴上或平行于坐标轴的线段的长度怎样计算?知识准备例1. 已知A(-1,0),B(2,0),C(1,2) 求S△ABC 思考:
如何选择底边?长度怎样计算?
高呢?长度是多少?自主探究例1.已知A(-1,0),B(2,0),C(1,2) 求S△ABC 解:过C作CD⊥x轴于D,
∵ C(1,2)
∴ CD=2
∵ A(-1,0),B(2,0)
∴ AB=3
∴ S△ABC=技巧:
选择坐标轴上的边为底边例2.已知A(-2,2),B(1,1),C(1,-2) 求S△ABC 思考:
如何选择底边?长度怎样计算?
如何作高?高长是多少?变式例题例2.已知A(-2,2),B(1,1),C(1,-2) 求S△ABC口述解题过程技巧:
选择与坐标轴平行的边为底边例3.已知A(-1,3),B(-3,-1),C(2,1) 求S△ABC 思考:
若按公式法,底边、高的长度容易计算吗?
该怎么办呢?合作探究要注意听讲哟!那个同学
若三角形三边与坐标轴都不平行时,将三角形补成一个边与坐标轴平行的长方形或梯形。
---割补法求面积例3.已知A(-1,3),B(-3,-1),C(2,1) 求S△ABC 在坐标系中求三角形面积时,要依据边的位置选择计算方法:
当至少有一边在坐标轴上或与坐标轴平行时,直接用公式法求面积,否则要利用图形割补法求面积。归纳总结本节课你学会了什么?还有什么困惑?温馨提示一、已知A(1,0), B(-1,2),点C在x轴上,△ABC的面积为3,
求C点坐标。应用拓展课后作业《全能学案》P56 第1--7题;二、收集与三角形面积相关的结论。同学们
:不断努力哟!
