安徽省六安市裕安区九年级数学下册24.5三角形的内切圆课件(新版)沪科版
文档属性
| 名称 | 安徽省六安市裕安区九年级数学下册24.5三角形的内切圆课件(新版)沪科版 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-27 00:00:00 | ||
图片预览



文档简介
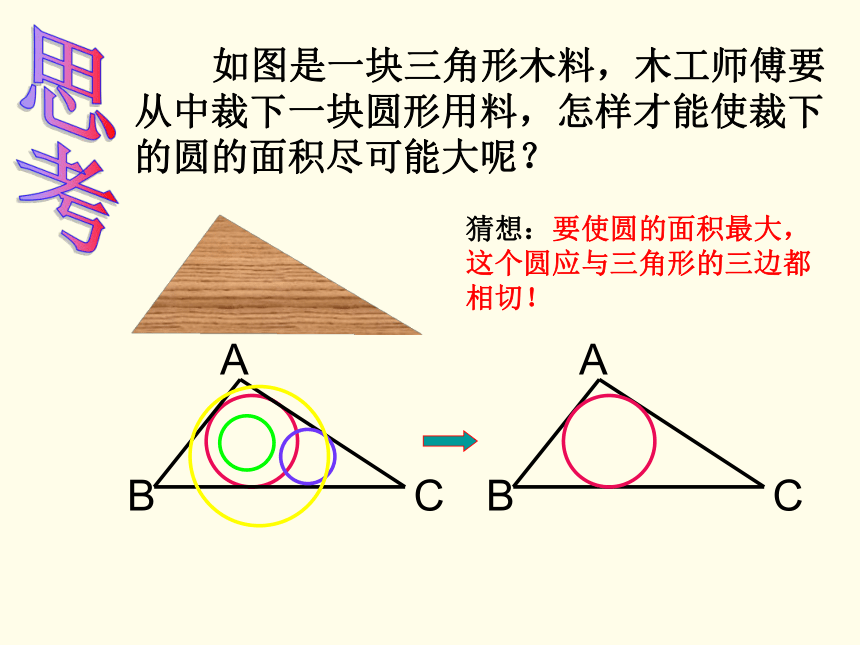
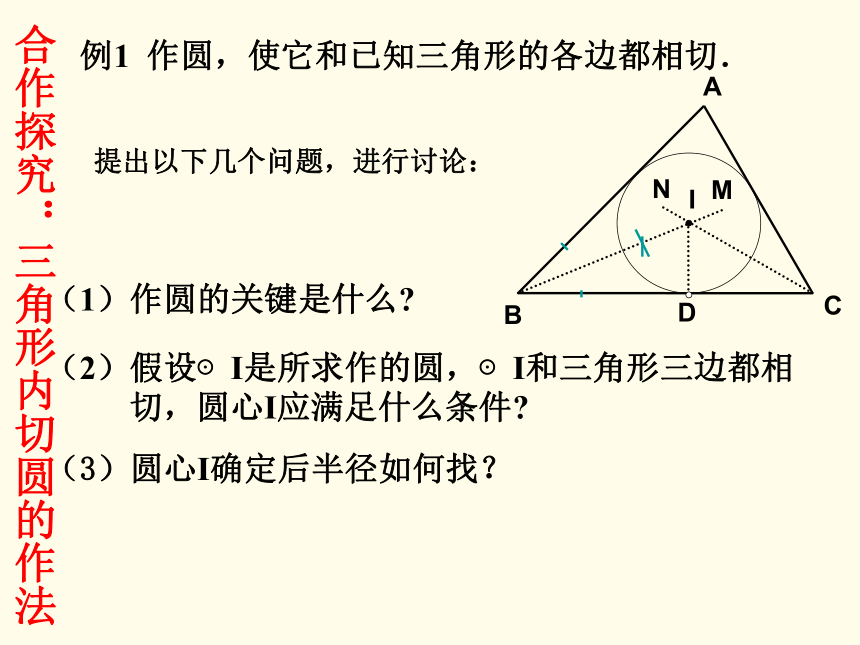
课件16张PPT。24.5 三角形的内切圆思考猜想:要使圆的面积最大,这个圆应与三角形的三边都相切!合作探究:三角形内切圆的作法例1 作圆,使它和已知三角形的各边都相切.(1)作圆的关键是什么?提出以下几个问题,进行讨论:(2)假设⊙I是所求作的圆,⊙I和三角形三边都相
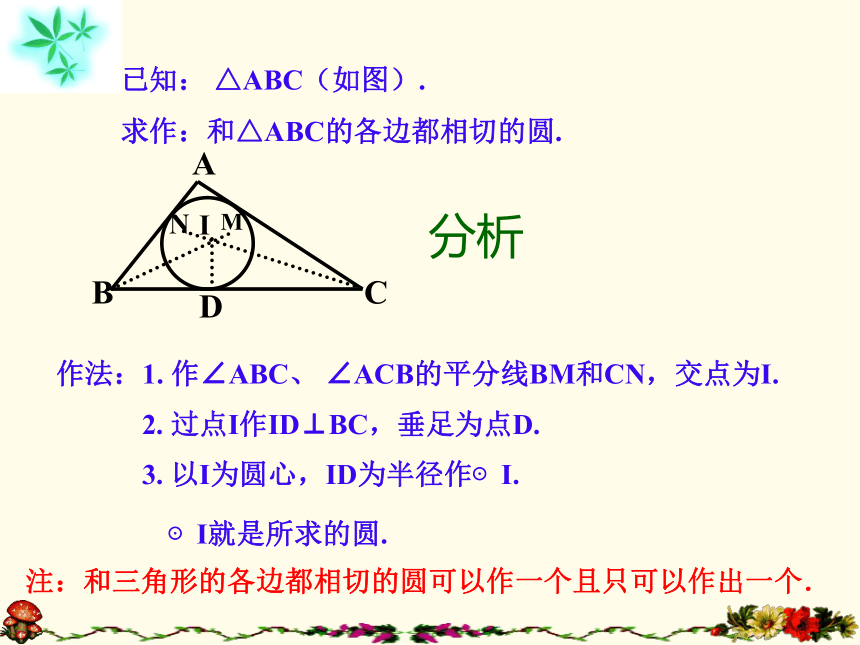
切,圆心I应满足什么条件?(3)圆心I确定后半径如何找?ABCIMND已知: △ABC(如图).
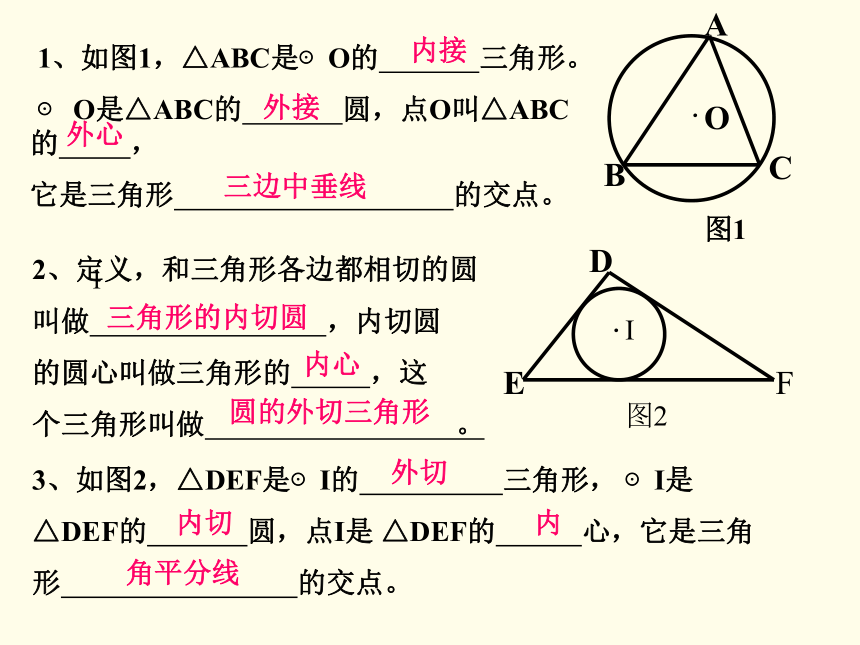
求作:和△ABC的各边都相切的圆.作法:1. 作∠ABC、 ∠ACB的平分线BM和CN,交点为I.ID分析2. 过点I作ID⊥BC,垂足为点D.3. 以I为圆心,ID为半径作⊙I.⊙I就是所求的圆.注:和三角形的各边都相切的圆可以作一个且只可以作出一个.三角形的内切圆的概念 和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心是三角形三个内角的角平分线的交点 1、如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线13、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。2、定义,和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。三角形的内切圆内心圆的外切三角形外切内切内角平分线三角形内心的性质:1. 三角形的内心到三角形各边的距离相等;
2. 三角形的内心在三角形的角平分线上. 1. 三角形的外心到三角形各个顶点的距离相等;
2. 三角形的外心在三角形三边的垂直平分线上. 三角形外心的性质:三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形的三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.oABC(2)若∠A=80 °,则∠BOC = 度.
(3)若∠BOC=100 °,则∠A = 度.解:13020(1)∵点O是△ABC的内心,∴ ∠BOC=180 °-(∠1+ ∠3)= 180 °-(25°+ 35 °)=120 °理由: ∵点O是△ABC的内心,(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由.在△OBC中,∠BOC =180 °-( ∠1+ ∠3 )例1 如图,点I和O分别是△ABC的内心和外心,若∠BOA=140°,求∠BIA的度数。能 力 提 升.ABCabcrr =a+b-c2例 直角三角形的两直角边分别是5cm,12cm .则其内切圆的半径为______.rO已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,求求其内切圆O的半径长.2EDOBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长.ABCFDExx13-x13-x9-x9-x∴(13-x)+(9-x)=14.略解:设AF=x,则BF=13-x.由切线长定理,知AE=AF=x,BD=BF=13-x,
DC=EC=9-x.又∵BD+CD=14,解得x=4.答:AF=4,
BD=9,
CE=5.∴AF=4,BD=9,CE=5.探讨:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?
解:AD+AF+BD+BE+CE+CF=L
2AD+2BE+2CE=L
2AD=L-2(BE+CE)
AD=AF=?
BD=BE?
CE=CF=?
CDEF三角形面积
(L为三角形周长,r为内切圆半径)r
切,圆心I应满足什么条件?(3)圆心I确定后半径如何找?ABCIMND已知: △ABC(如图).
求作:和△ABC的各边都相切的圆.作法:1. 作∠ABC、 ∠ACB的平分线BM和CN,交点为I.ID分析2. 过点I作ID⊥BC,垂足为点D.3. 以I为圆心,ID为半径作⊙I.⊙I就是所求的圆.注:和三角形的各边都相切的圆可以作一个且只可以作出一个.三角形的内切圆的概念 和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心是三角形三个内角的角平分线的交点 1、如图1,△ABC是⊙O的 三角形。
⊙ O是△ABC的 圆,点O叫△ABC的 ,
它是三角形 的交点。外接内接外心三边中垂线13、如图2,△DEF是⊙I的 三角形, ⊙I是
△DEF的 圆,点I是 △DEF的 心,它是三角
形 的交点。2、定义,和三角形各边都相切的圆
叫做 ,内切圆
的圆心叫做三角形的 ,这
个三角形叫做 。三角形的内切圆内心圆的外切三角形外切内切内角平分线三角形内心的性质:1. 三角形的内心到三角形各边的距离相等;
2. 三角形的内心在三角形的角平分线上. 1. 三角形的外心到三角形各个顶点的距离相等;
2. 三角形的外心在三角形三边的垂直平分线上. 三角形外心的性质:三角形三边
中垂线的交
点1.OA=OB=OC
2.外心不一定在三角形的内部.三角形的三条
角平分线的
交点1.到三边的距离
相等;
2.OA、OB、OC分别平分∠BAC、∠ABC、∠ACB
3.内心在三角形内部.oABC(2)若∠A=80 °,则∠BOC = 度.
(3)若∠BOC=100 °,则∠A = 度.解:13020(1)∵点O是△ABC的内心,∴ ∠BOC=180 °-(∠1+ ∠3)= 180 °-(25°+ 35 °)=120 °理由: ∵点O是△ABC的内心,(4)试探索: ∠A与∠BOC之间存在怎样的数量关系?请说明理由.在△OBC中,∠BOC =180 °-( ∠1+ ∠3 )例1 如图,点I和O分别是△ABC的内心和外心,若∠BOA=140°,求∠BIA的度数。能 力 提 升.ABCabcrr =a+b-c2例 直角三角形的两直角边分别是5cm,12cm .则其内切圆的半径为______.rO已知:如图,在Rt△ABC中,∠C=90°,边BC、AC、AB的长分别为a、b、c,求求其内切圆O的半径长.2EDOBA? 探讨3:
设△ABC是直角三角形,∠C=90°,它
的内切圆的半径为r,△ABC 的各边长分别为a、b、c,试探讨r与a、b、c的关系.
C┛cbaFEDr结论:已知:在△ABC中,BC=14,AC=9,AB=13,它的内切圆分别和BC、AC、AB切于点D、E、F,求AF、BD和CE的长.ABCFDExx13-x13-x9-x9-x∴(13-x)+(9-x)=14.略解:设AF=x,则BF=13-x.由切线长定理,知AE=AF=x,BD=BF=13-x,
DC=EC=9-x.又∵BD+CD=14,解得x=4.答:AF=4,
BD=9,
CE=5.∴AF=4,BD=9,CE=5.探讨:
设△ABC 的内切圆的半径为r,△ABC 的各边长之和为L,△ABC 的面积S,我们会有什么结论?
解:AD+AF+BD+BE+CE+CF=L
2AD+2BE+2CE=L
2AD=L-2(BE+CE)
AD=AF=?
BD=BE?
CE=CF=?
CDEF三角形面积
(L为三角形周长,r为内切圆半径)r
