数学思考例1 2 3 课件(31张)
文档属性
| 名称 | 数学思考例1 2 3 课件(31张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 21:36:11 | ||
图片预览









文档简介
(共31张PPT)
4. 数学思考
探究模式的策略 例1
整理和复习
一、引入情境,探究规律
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
(二)合作探究,分享方法
预设1:
一、引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
不重复,不遗漏。
问题:想一想,按顺序画有什么好处?
预设2:
5+4+3+2+1=15(条)
(二)合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
(二)合作探究,分享方法
一、引入情境,探究规律
幸亏只有6个点,要是有600个点就惨了!
对呀,我们找找规律吧!从最少的2个点开始。
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
问题:观察“点数”和“增加条数”,你发现了什么规律?
(二)合作探究,分享方法
一、引入情境,探究规律
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
(二)合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
二、应用规律,解决问题
=(1+11)+(2+10)+(3+9)
+(4+8)+(5+7)+6
问题:按照简单的方法计算,你发现了什么?
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×5+6
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
二、应用规律,解决问题
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)
+……+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
三、巩固练习,提升认识
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
三、巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
三、巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
问题:遇到复杂的问题,你可以怎样思考?
三、巩固练习,提升认识
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
四、布置作业
作业:第103页练习二十二,
第1、2、3、4题。
4. 数学思考
列表的方法 例2
整理和复习
一、引入情境,探究新知
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
一、引入情境,探究新知
(二)解决问题,分享方法
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
用列表的方法试一试!
一、引入情境,探究新知
(二)解决问题,分享方法
问题:1. A可能和谁是同班?
2. 请你根据表格继续推理,B、C可能和谁是同班呢?
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
√ √ √
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
×
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √ √
√ √√
×
√×
列表的方法真简单!
做一做。
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
问题:你想用什么方法解决这个问题?
二、巩固练习,提升认识
二、巩固练习,提升认识
列表是解决复杂问题的好方法。
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
军人
×
×
√
√
√
√
三、布置作业
作业:第103页练习二十二,第5、7、8题。
4. 数学思考
推理的思想 例3
整理和复习
(1)已知 + =24, = + + 。
求 和 的值。
一、引入情境,探究方法
(一)出示信息,明确问题
问题: 是什么意思?
=
+
+
、 、 、 、 各代表一个数。
1.
2. 圈起来的这一步运用了什么数学思想?
问题:1. 请你独立解决这个问题。
等量代换
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
一、引入情境,探究方法
(二)独立思考,分享方法
(2)
+
=
160,
是否等于 ?
+
=
160。
问题:1. 请你独立思考,然后跟同伴说说你的想法。
2. 在推理的过程中,你运用了什么知识?
+
=
+
=
-
+
=
+
-
(二)独立思考,分享方法
一、引入情境,探究方法
问题:什么是平角?平角与直线有什么区别?
2. 如右图,两条直线相交于点O。
∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。
一、引入情境,探究方法
(二)独立思考,分享方法
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
(2)你能推出∠1=∠3吗?
∠1+∠2
=
180°
∠2+∠3
=
180°
∠1+∠2
=
∠2+∠3
∠3
∠1
=
=
-∠2
∠1+∠2
∠2+∠3
-∠2
问题:1. 请你独立思考,说说你的想法。
2. 在推理的过程中,你运用了什么知识?
一、引入情境,探究方法
(二)独立思考,分享方法
1. 找等量关系
2. 等量代换
3. 合情推理
问题:对看似不相关的独立的信息,在解决问题时你
会怎样思考呢?
二、梳理方法,提升认识
三、布置作业
作业:第104页练习二十二,第10题。
4. 数学思考
探究模式的策略 例1
整理和复习
一、引入情境,探究规律
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
最多有2个点在同一条直线上,那么6个点可以连多少条线段?8个点呢?
(二)合作探究,分享方法
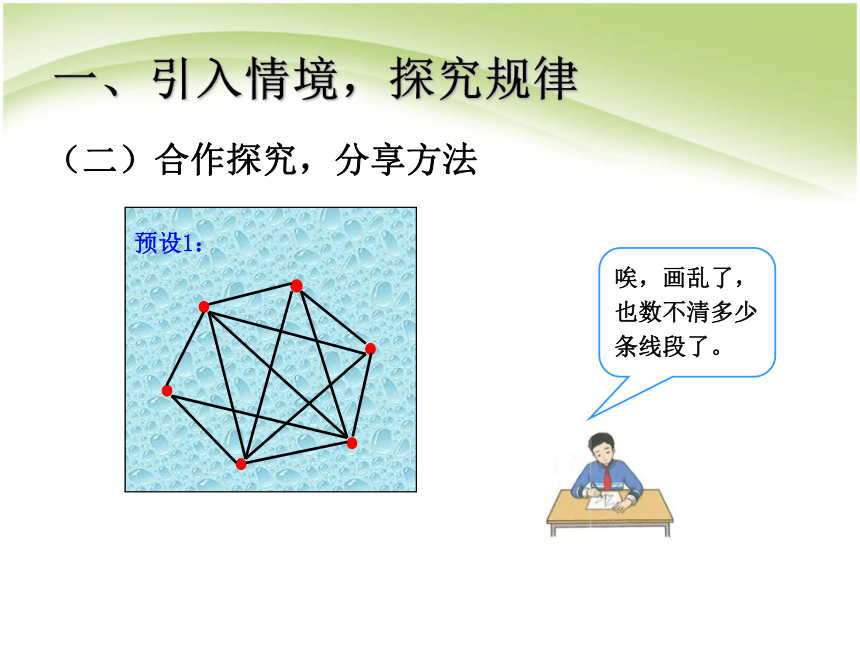
预设1:
一、引入情境,探究规律
唉,画乱了,也数不清多少条线段了。
不重复,不遗漏。
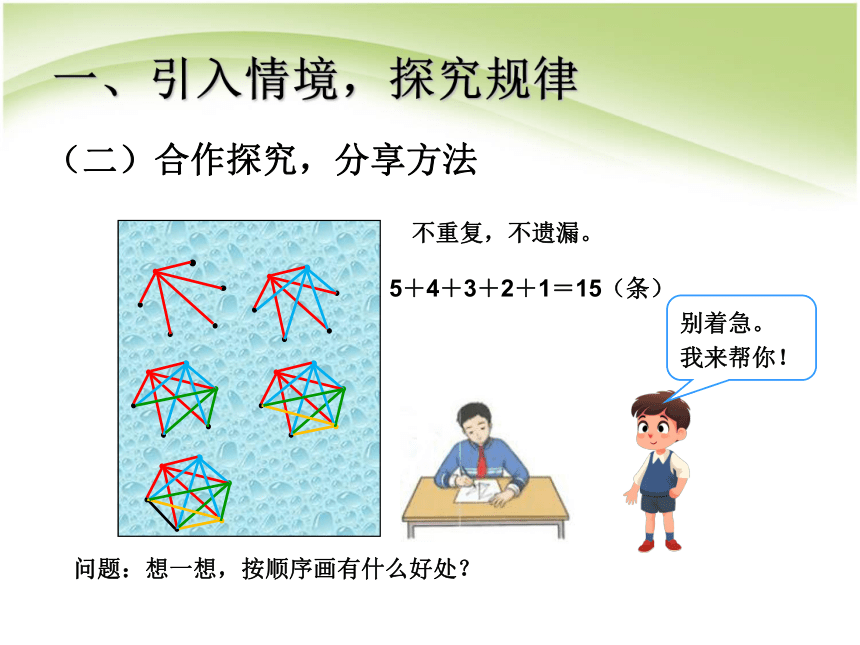
问题:想一想,按顺序画有什么好处?
预设2:
5+4+3+2+1=15(条)
(二)合作探究,分享方法
一、引入情境,探究规律
别着急。
我来帮你!
(二)合作探究,分享方法
一、引入情境,探究规律
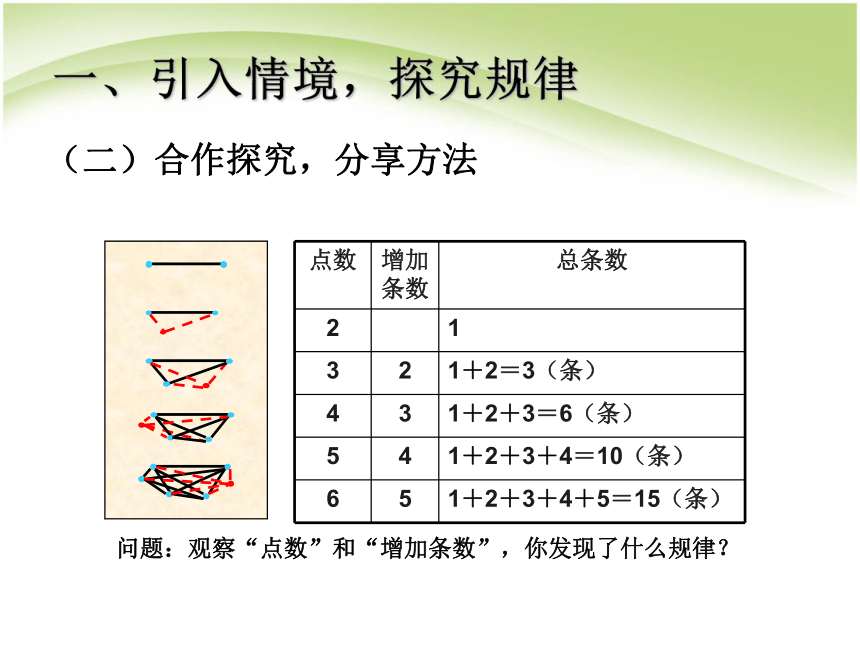
幸亏只有6个点,要是有600个点就惨了!
对呀,我们找找规律吧!从最少的2个点开始。
点数 增加条数 总条数
2 1
3 2 1+2=3(条)
4 3 1+2+3=6(条)
5 4 1+2+3+4=10(条)
6 5 1+2+3+4+5=15(条)
问题:观察“点数”和“增加条数”,你发现了什么规律?
(二)合作探究,分享方法
一、引入情境,探究规律
1+2+3+4+5+6+7
问题:1. 按照规律,8个点能连几条线段?
2. 为什么有8个点,列式却依次加到7呢?
(二)合作探究,分享方法
一、引入情境,探究规律
3. 想一想,能用简单方法计算吗?
=(1+7)+(2+6)+(3+5)+4
=28(条) ——8个点
=8×3+4
二、应用规律,解决问题
=(1+11)+(2+10)+(3+9)
+(4+8)+(5+7)+6
问题:按照简单的方法计算,你发现了什么?
1+2+3+4+5+6+7+8+9+10+11
=66(条) ——12个点
=12×5+6
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
二、应用规律,解决问题
1. 根据规律,你知道12个点、20个点能连多少条线段吗?
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19
=(1+19)+(2+18)+(3+17)
+……+(8+12)+(9+11)+10
=20×9+10
=190(条) ——20个点
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
问题:1. 你想怎样解决这个问题?
2. 从最简单的数据开始,数一数每幅图各有多少个棋子?
三、巩固练习,提升认识
3. 在数的过程中,你发现了什么?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
问题:1. 第7幅图每行有几个棋子?有几行?共有几个棋子?
3. 第15幅图共有几个棋子?
三、巩固练习,提升认识
7×7=49(个)
15×15=225(个)
观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
2. 每边的棋子数与图形的序号有什么关系?
观察下图,想一想。
(2)第n幅图有多少个棋子?
问题:第n幅图每边有多少个棋子?一共有多少个棋子?
三、巩固练习,提升认识
每行的棋子数×行数=棋子总数
n × n = 棋子总数
n2 =棋子总数
问题:遇到复杂的问题,你可以怎样思考?
三、巩固练习,提升认识
3. 有序思考
2. 画图、枚举
1. 化繁为简
4. 探究规律
四、布置作业
作业:第103页练习二十二,
第1、2、3、4题。
4. 数学思考
列表的方法 例2
整理和复习
一、引入情境,探究新知
(一)出示信息,明确问题
问题:你想怎样解决这个问题?动手试一试吧。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?
一、引入情境,探究新知
(二)解决问题,分享方法
用数字“1” 表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
用列表的方法试一试!
一、引入情境,探究新知
(二)解决问题,分享方法
问题:1. A可能和谁是同班?
2. 请你根据表格继续推理,B、C可能和谁是同班呢?
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
√ √ √
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √
×
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
√ √ √
√ √√
×
√×
列表的方法真简单!
做一做。
王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。
请问:他们的职业各是什么?
问题:你想用什么方法解决这个问题?
二、巩固练习,提升认识
二、巩固练习,提升认识
列表是解决复杂问题的好方法。
王阿姨 刘阿姨 丁叔叔 李叔叔
工人
教师
军人
×
×
√
√
√
√
三、布置作业
作业:第103页练习二十二,第5、7、8题。
4. 数学思考
推理的思想 例3
整理和复习
(1)已知 + =24, = + + 。
求 和 的值。
一、引入情境,探究方法
(一)出示信息,明确问题
问题: 是什么意思?
=
+
+
、 、 、 、 各代表一个数。
1.
2. 圈起来的这一步运用了什么数学思想?
问题:1. 请你独立解决这个问题。
等量代换
+ = 24
= 6
+
= 24
+
+
=
+
+
=18
一、引入情境,探究方法
(二)独立思考,分享方法
(2)
+
=
160,
是否等于 ?
+
=
160。
问题:1. 请你独立思考,然后跟同伴说说你的想法。
2. 在推理的过程中,你运用了什么知识?
+
=
+
=
-
+
=
+
-
(二)独立思考,分享方法
一、引入情境,探究方法
问题:什么是平角?平角与直线有什么区别?
2. 如右图,两条直线相交于点O。
∠1 和∠2 、∠2和∠3 、∠3和∠4 、∠4和∠1,一共能组成4个平角。
一、引入情境,探究方法
(二)独立思考,分享方法
(1)每相邻两个角可以组成一个平角,一共能组成几个平角?
(2)你能推出∠1=∠3吗?
∠1+∠2
=
180°
∠2+∠3
=
180°
∠1+∠2
=
∠2+∠3
∠3
∠1
=
=
-∠2
∠1+∠2
∠2+∠3
-∠2
问题:1. 请你独立思考,说说你的想法。
2. 在推理的过程中,你运用了什么知识?
一、引入情境,探究方法
(二)独立思考,分享方法
1. 找等量关系
2. 等量代换
3. 合情推理
问题:对看似不相关的独立的信息,在解决问题时你
会怎样思考呢?
二、梳理方法,提升认识
三、布置作业
作业:第104页练习二十二,第10题。
