2017九年级数学上册25.1比例线段导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.1比例线段导学案(新版)冀教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 468.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-27 00:00:00 | ||
图片预览



文档简介
25.1
比例线段
学习目标:
学习并掌握比例线段的相关概念并学会运用.
掌握比例的性质,并能够运用比例的性质求值.
了解黄金分割的意义.
学习重点:比例线段的概念及性质.
学习难点:黄金分割的运用.
知识链接
1
.已知线段AB和CD的长度分别是2cm,6cm,则AB和CD的比是_______,表示为_______.
2.小学里已学过了比例的有关知识,那么,什么是比例?怎样表示比例?说出比例中各部分
的名称,比例的基本性质是什么?
新知预习
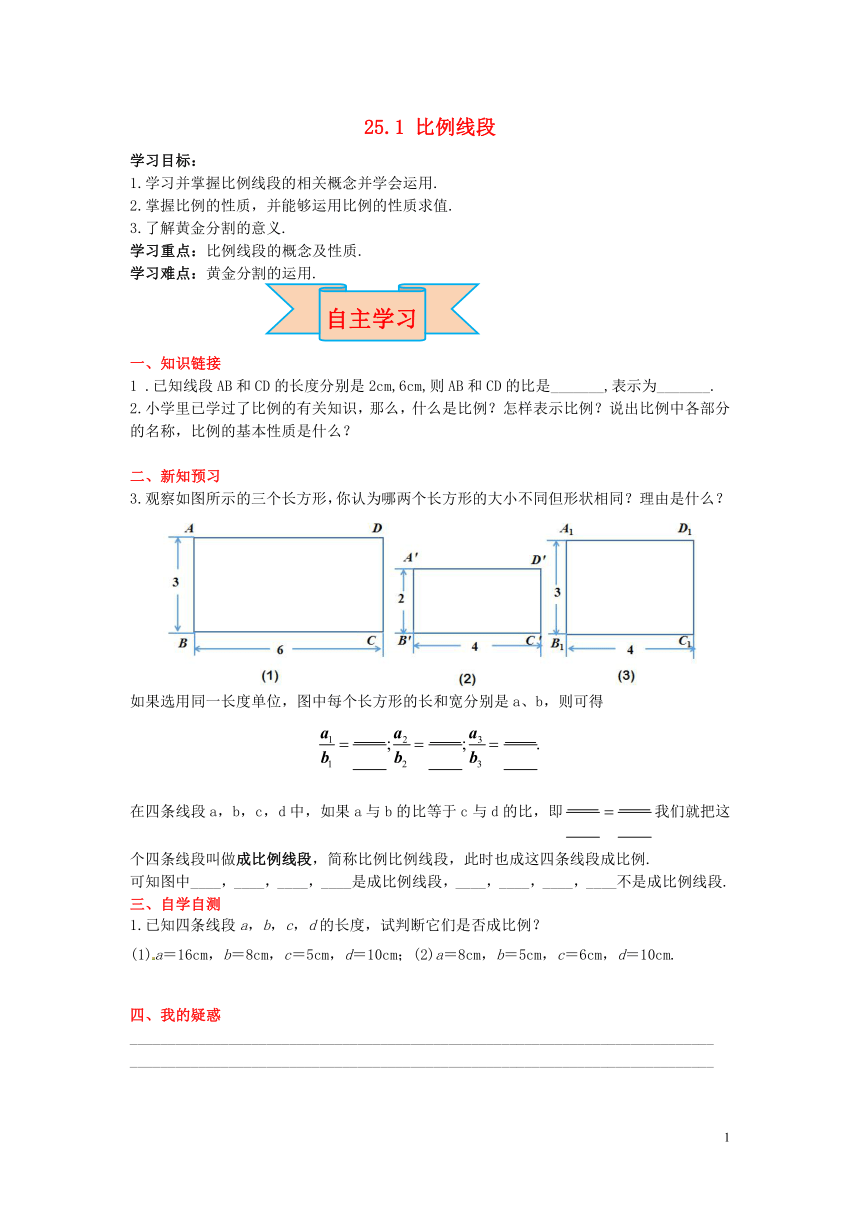
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
如果选用同一长度单位,图中每个长方形的长和宽分别是a、b,则可得
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即我们就把这个四条线段叫做成比例线段,简称比例比例线段,此时也成这四条线段成比例.
可知图中____,____,____,____是成比例线段,____,____,____,____不是成比例线段.
三、自学自测
1.已知四条线段a,b,c,d的长度,试判断它们是否成比例?
(1)a=16cm,b=8cm,c=5cm,d=10cm;(2)a=8cm,b=5cm,c=6cm,d=10cm.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:成比例线段
例1:下列四组线段中,是成比例线段的是( )
A.3cm,4cm,5cm,6cm
B.4cm,8cm,3cm,5cm
C.5cm,15cm,2cm,6cm
D.8cm,4cm,1cm,3cm
【归纳总结】判断四条线段是否成比例的方法:(1)把四条线段按从小到大顺序排好,计算前两条线段的比和后两条线段的比,看是否相等做出判断;(2)把四条线段按从小到大顺序排好,计算前后两个数的积与中间两个数的积,看是否相等作出判断.
【针对训练】
1.已知:四条线段a、b、c、d,其中a=3cm,b=8cm,c=6cm.
(1)若a、b、c、d是成比例线段,求线段d的长度;
(2)若b、a、c、d是成比例线段,求线段d的长度.
在比例尺为1:50
000的地图上,量得甲、乙两地的距离是3cm,则甲、乙两地的实际距离是 m.
思路分析:根据比例尺=图上距离/实际距离,列方程求解.
探究点2:比例的性质
比例的基本性质
问题1:如果a,b,c,d四个数满足,那么ad和bc相等吗?并说明理由
答:________.
理由如下:
∵b≠0,d≠0,∴bd_______0.
∴在等式两边同时乘以bd,得____________.
即若,则ad=bc.
问题2:试说出问题1中结论的逆命题,它是真命题吗?如何证明?
逆命题是:如果ad=bc,那么_______.
请仿照问题1证明:
【归纳】比例的基本性质:
如果ad=bc,那么________(b,d≠0).
例2:已知=,求的值.
解:解法1:由比例的基本性质,
得____________.
∴a=____b,∴=____.
解法2:(倒数法)由=,得________=7,
∴____________,∴=_______.
【归纳总结】利用比例的基本性质,把比例式转化成等积式,再用含有其中一个字母的代数式表示另一个字母,然后利用代入法或化成方程求解,这是解决比例问题常见的方法.
(二)等比的性质
我们知道,由
试猜想:
并证明你的猜想.
【针对训练】
1.已知a:b:c=3:4:5,求的值.
2.已知===2,且b+d+f≠0,求的值.
3.若a,b,c都是不等于零的数,且===k,求k的值.
探究点3:黄金分割
问题:
1.如图,在五角星图案中,用刻度尺分别测量线段AC、BC的程度,然后计算,它们的值相等吗?
已知线段AB的长度为1个单位,在线段AB上找一点C,使较短的线段BC与较长的线段AC的比等于AC与原线段的比,即使成立,求此时线段AC的长.
3.你能在线段上画出点C的大概位置吗?这样的点有几个?
【归纳】在线段AB上有一点C,如果点C把AB分成的两条线段AC和BC满足,那么称线段AB被点C黄金分割,点C称为线段AB的黄金分割点,AC/AB称为黄金分割点.
例3:已知M是线段AB的黄金分割点,MA是被分线段AB中较长的线段,且MA=-1,求原线段AB的长.
【归纳总结】把一条线段黄金分割后,原线段、较长线段、较短线段之间有固定的比值关系,只要知道其中一条线段的长度,就可以求出另外两条线段的长度.
【针对训练】
1.已知线段AB=6,点C为线段AB的黄金分割点,求下列各式的值:
AC-BC;
(2)AC·BC.
2.在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
二、课堂小结
比例线段
内容
运用策略
线段的比
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即我们就把这个四条线段叫做成比例线段,
判断四条线段是否成比例,首先要将线段的单位同一,然后按照从小到大的顺序排列,计算前后两个数的积与中间两个数的积,看是否相等作出判断.
比例的性质
①如果,那么________;②如果ad=bc,那么________;③等比的性质:____________.
把比例式转化成等积式,再用含有其中一个字母的代数式表示另一个字母,然后利用代入法或化成方程求解,这是解决比例问题常见的方法.
黄金分割
①一条线段的的黄金分割点有___个;②黄金分割比为__________.
如果点C是线段AB的黄金分割点,且AC>BC,则AC=______AB,BC=_______AB.
1.下列各组数中一定成比例的是(
)
A.2,3,4,5.
B.-1,2,-2,4.
C.-2,
1,
2,0.
D.a,2b,c,2d.
2.已知一个比例式的比例外项为m,n,比例内项为p,q,则下面所给的比例式正确的是(
)
A.
m:n=p:q
B.m:p=n:q.
C.m:q=n:p
D.m:p=q:n.
3.若点C是线段AB的黄金分割点,且AB=2,则AC=( )
A.-1
B.3-
C.
D.-1或3-
4.已知线段x=12cm,y=4cm.线段x和y的比例中项为a,则a=________cm.
5.已知三条线段的长度分别为1cm,cm,2cm,请你再给出一条线段,使得这四条线段能够组成一个比例式.
6.已知==≠0.
(1)若a+b+c=24,求a,b,c的值;(2)求的值.
7..如图,已知线段AB.
(1)经过点B作BD⊥AB,使BD=AB.
(2)连结AD,在DA上截取DE=DB.
(3)在AB上截取AC=AE.
请你根据以上作法,证明点C是线段AB的黄金分割点.
当堂检测参考答案:
B
2.D
3.D
4.4
5.所给的线段长为xcm,则有
①=,x=;②=,x=;
③=,x=2.
故再给出的一条线段长应为cm或cm或2cm.
6.(1)设===k(k≠0),
则a=3k,b=4k,c=5k,
所以a+b+c=3k+4k+5k=12k=24,
解得k=2.
所以a=3k=6,b=4k=8,c=5k=10.
(2)由(1)得a=3k,b=4k,c=5k,
所以==-.
7.设AB=2x,则BD=DE=x,根据勾股定理,得AD===x,
则AC=AE=x-x=(-1)x.
∵=,
∴点C是线段AB的黄金分割点.
自主学习
合作探究
当堂检测
PAGE
1
比例线段
学习目标:
学习并掌握比例线段的相关概念并学会运用.
掌握比例的性质,并能够运用比例的性质求值.
了解黄金分割的意义.
学习重点:比例线段的概念及性质.
学习难点:黄金分割的运用.
知识链接
1
.已知线段AB和CD的长度分别是2cm,6cm,则AB和CD的比是_______,表示为_______.
2.小学里已学过了比例的有关知识,那么,什么是比例?怎样表示比例?说出比例中各部分
的名称,比例的基本性质是什么?
新知预习
观察如图所示的三个长方形,你认为哪两个长方形的大小不同但形状相同?理由是什么?
如果选用同一长度单位,图中每个长方形的长和宽分别是a、b,则可得
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即我们就把这个四条线段叫做成比例线段,简称比例比例线段,此时也成这四条线段成比例.
可知图中____,____,____,____是成比例线段,____,____,____,____不是成比例线段.
三、自学自测
1.已知四条线段a,b,c,d的长度,试判断它们是否成比例?
(1)a=16cm,b=8cm,c=5cm,d=10cm;(2)a=8cm,b=5cm,c=6cm,d=10cm.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:成比例线段
例1:下列四组线段中,是成比例线段的是( )
A.3cm,4cm,5cm,6cm
B.4cm,8cm,3cm,5cm
C.5cm,15cm,2cm,6cm
D.8cm,4cm,1cm,3cm
【归纳总结】判断四条线段是否成比例的方法:(1)把四条线段按从小到大顺序排好,计算前两条线段的比和后两条线段的比,看是否相等做出判断;(2)把四条线段按从小到大顺序排好,计算前后两个数的积与中间两个数的积,看是否相等作出判断.
【针对训练】
1.已知:四条线段a、b、c、d,其中a=3cm,b=8cm,c=6cm.
(1)若a、b、c、d是成比例线段,求线段d的长度;
(2)若b、a、c、d是成比例线段,求线段d的长度.
在比例尺为1:50
000的地图上,量得甲、乙两地的距离是3cm,则甲、乙两地的实际距离是 m.
思路分析:根据比例尺=图上距离/实际距离,列方程求解.
探究点2:比例的性质
比例的基本性质
问题1:如果a,b,c,d四个数满足,那么ad和bc相等吗?并说明理由
答:________.
理由如下:
∵b≠0,d≠0,∴bd_______0.
∴在等式两边同时乘以bd,得____________.
即若,则ad=bc.
问题2:试说出问题1中结论的逆命题,它是真命题吗?如何证明?
逆命题是:如果ad=bc,那么_______.
请仿照问题1证明:
【归纳】比例的基本性质:
如果ad=bc,那么________(b,d≠0).
例2:已知=,求的值.
解:解法1:由比例的基本性质,
得____________.
∴a=____b,∴=____.
解法2:(倒数法)由=,得________=7,
∴____________,∴=_______.
【归纳总结】利用比例的基本性质,把比例式转化成等积式,再用含有其中一个字母的代数式表示另一个字母,然后利用代入法或化成方程求解,这是解决比例问题常见的方法.
(二)等比的性质
我们知道,由
试猜想:
并证明你的猜想.
【针对训练】
1.已知a:b:c=3:4:5,求的值.
2.已知===2,且b+d+f≠0,求的值.
3.若a,b,c都是不等于零的数,且===k,求k的值.
探究点3:黄金分割
问题:
1.如图,在五角星图案中,用刻度尺分别测量线段AC、BC的程度,然后计算,它们的值相等吗?
已知线段AB的长度为1个单位,在线段AB上找一点C,使较短的线段BC与较长的线段AC的比等于AC与原线段的比,即使成立,求此时线段AC的长.
3.你能在线段上画出点C的大概位置吗?这样的点有几个?
【归纳】在线段AB上有一点C,如果点C把AB分成的两条线段AC和BC满足,那么称线段AB被点C黄金分割,点C称为线段AB的黄金分割点,AC/AB称为黄金分割点.
例3:已知M是线段AB的黄金分割点,MA是被分线段AB中较长的线段,且MA=-1,求原线段AB的长.
【归纳总结】把一条线段黄金分割后,原线段、较长线段、较短线段之间有固定的比值关系,只要知道其中一条线段的长度,就可以求出另外两条线段的长度.
【针对训练】
1.已知线段AB=6,点C为线段AB的黄金分割点,求下列各式的值:
AC-BC;
(2)AC·BC.
2.在人体躯干与身高的比例上,肚脐是理想的黄金分割点,即比值越接近0.618越给人以美感.小明的妈妈脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该穿多高的高跟鞋看起来会更美?
二、课堂小结
比例线段
内容
运用策略
线段的比
在四条线段a,b,c,d中,如果a与b的比等于c与d的比,即我们就把这个四条线段叫做成比例线段,
判断四条线段是否成比例,首先要将线段的单位同一,然后按照从小到大的顺序排列,计算前后两个数的积与中间两个数的积,看是否相等作出判断.
比例的性质
①如果,那么________;②如果ad=bc,那么________;③等比的性质:____________.
把比例式转化成等积式,再用含有其中一个字母的代数式表示另一个字母,然后利用代入法或化成方程求解,这是解决比例问题常见的方法.
黄金分割
①一条线段的的黄金分割点有___个;②黄金分割比为__________.
如果点C是线段AB的黄金分割点,且AC>BC,则AC=______AB,BC=_______AB.
1.下列各组数中一定成比例的是(
)
A.2,3,4,5.
B.-1,2,-2,4.
C.-2,
1,
2,0.
D.a,2b,c,2d.
2.已知一个比例式的比例外项为m,n,比例内项为p,q,则下面所给的比例式正确的是(
)
A.
m:n=p:q
B.m:p=n:q.
C.m:q=n:p
D.m:p=q:n.
3.若点C是线段AB的黄金分割点,且AB=2,则AC=( )
A.-1
B.3-
C.
D.-1或3-
4.已知线段x=12cm,y=4cm.线段x和y的比例中项为a,则a=________cm.
5.已知三条线段的长度分别为1cm,cm,2cm,请你再给出一条线段,使得这四条线段能够组成一个比例式.
6.已知==≠0.
(1)若a+b+c=24,求a,b,c的值;(2)求的值.
7..如图,已知线段AB.
(1)经过点B作BD⊥AB,使BD=AB.
(2)连结AD,在DA上截取DE=DB.
(3)在AB上截取AC=AE.
请你根据以上作法,证明点C是线段AB的黄金分割点.
当堂检测参考答案:
B
2.D
3.D
4.4
5.所给的线段长为xcm,则有
①=,x=;②=,x=;
③=,x=2.
故再给出的一条线段长应为cm或cm或2cm.
6.(1)设===k(k≠0),
则a=3k,b=4k,c=5k,
所以a+b+c=3k+4k+5k=12k=24,
解得k=2.
所以a=3k=6,b=4k=8,c=5k=10.
(2)由(1)得a=3k,b=4k,c=5k,
所以==-.
7.设AB=2x,则BD=DE=x,根据勾股定理,得AD===x,
则AC=AE=x-x=(-1)x.
∵=,
∴点C是线段AB的黄金分割点.
自主学习
合作探究
当堂检测
PAGE
1
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
