2017九年级数学上册25.2平行线分线段成比例导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.2平行线分线段成比例导学案(新版)冀教版 |  | |
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 18:10:40 | ||
图片预览

文档简介
25.2
平行线分线段成比例
学习目标:
学习并掌握平行线分线段成比例定理及其推论并学会运用.
2.能够运用平行线分线段成比例定理及推论解决问题.
学习重点:平行线分线段成比例定理及其推论.
学习难点:平行线分线段成比例定理及其推论的运用.
新知预习
问题1:如图①,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于点A1,A2,A3,B1,B2,B3.
利用勾股定理计算:
计算:
图①
图②
这些比值有什么关系?你有什么发现?
问题2:将l2向下平移到如图②的位置,直线m,n与l2的交点分别为A2,B2,你在上题中发现的规律还成立吗?如果将l2平移到其他位置呢?
【猜想】在平面上任意作三条平行线,用它们截两条直线,所截得的线段成比例吗?
【归纳】
二、自学自测
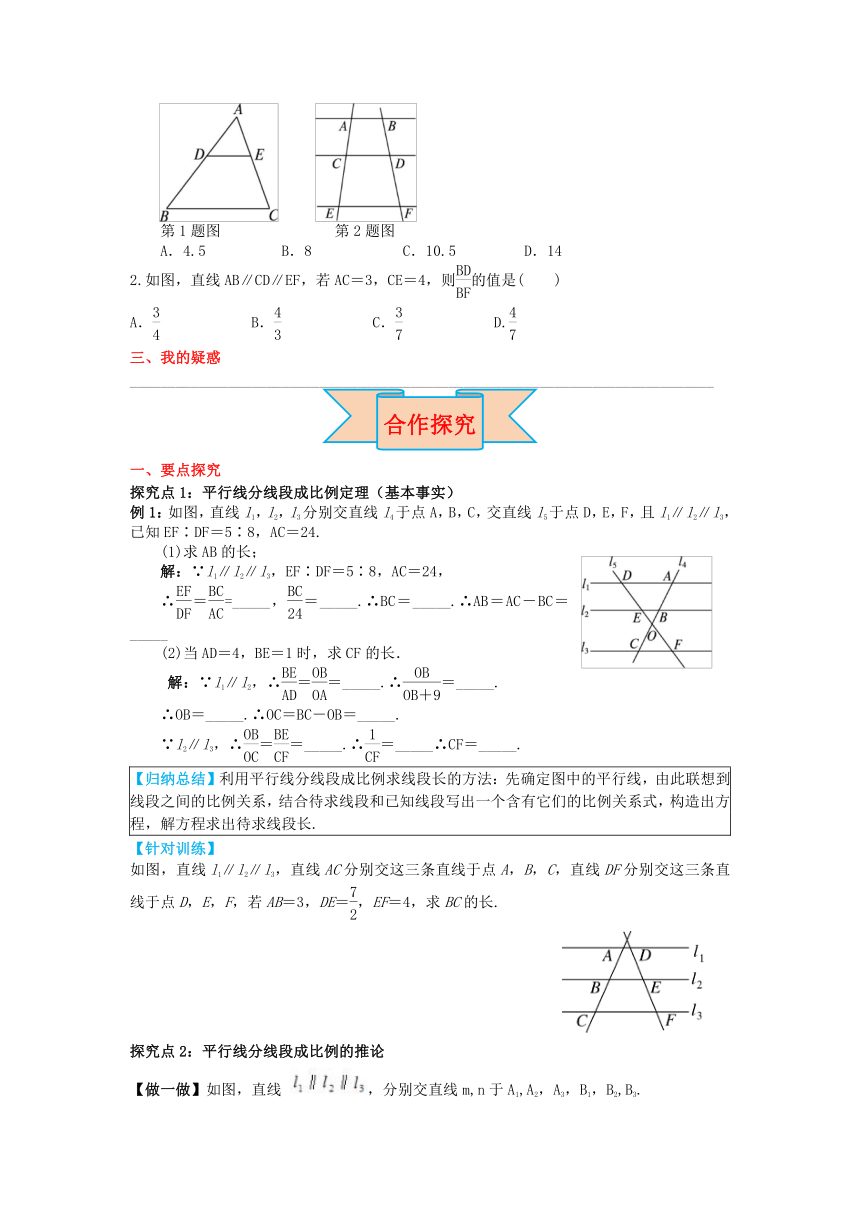
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,=,则EC的长是( )
第1题图
第2题图
A.4.5
B.8
C.10.5
D.14
2.如图,直线AB∥CD∥EF,若AC=3,CE=4,则的值是( )
A.
B.
C.
D.
三、我的疑惑
_____________________________________________________________________________
要点探究
探究点1:平行线分线段成比例定理(基本事实)
例1:如图,直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3,已知EF∶DF=5∶8,AC=24.
求AB的长;
解:∵l1∥l2∥l3,EF∶DF=5∶8,AC=24,
∴==_____,=_____.∴BC=_____.∴AB=AC-BC=_____
(2)当AD=4,BE=1时,求CF的长.
解:∵l1∥l2,∴==_____.∴=_____.
∴OB=_____.∴OC=BC-OB=_____.
∵l2∥l3,∴==_____.∴=_____∴CF=_____.
【归纳总结】利用平行线分线段成比例求线段长的方法:先确定图中的平行线,由此联想到线段之间的比例关系,结合待求线段和已知线段写出一个含有它们的比例关系式,构造出方程,解方程求出待求线段长.
【针对训练】
如图,直线l1∥l2∥l3,直线AC分别交这三条直线于点A,B,C,直线DF分别交这三条直线于点D,E,F,若AB=3,DE=,EF=4,求BC的长.
探究点2:平行线分线段成比例的推论
【做一做】如图,直线,分别交直线m,n于A1,A2,A3,B1,B2,B3.
图中有哪些成比例线段?
(2)
如果把图1中A1A3,B1B3.两条直线相交,交点刚落到上l1
,如图3所得的对应线段的比
________,依据是_____________________________.
(3)如果把图1中A1A3,B1B3.两条直线相交,交点刚落到上
l2,如图4所得的对应线段的比_________,依据是______________________________________.
【归纳】推论:
内容
字母表示
图例
推论1
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
EF∥BC
推论2
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.
为了便于记忆,平行中的等比例式可使用一些简单的形象化的语言:
例2:如图所示,在△ABC中,E,F,分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
解:
∵EF∥BC,
∴________________.
∵AE
=
7,
EB
=
5
,
FC
=
4.
∴AF=_________________.
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
解:
∵EF∥BC,
∴________________.
∵AB
=
10
,
AE
=
6
,
AF
=
5.
∴________________.
∴FC=AC
–
AF
=________________.
例3:如图,在△ABC的边AB上取一点D,在AC上取一点E,使得AD=AE,直线DE和BC的延长线相交于P,求证:=.
【思路提示】过点C作DE的平行线.
证明:
【归纳总结】在由平行线推出成比例线段的比例式时,要注意它们的相互位置关系,比例式不能写错,要把对应的线段写在对应的位置上.当题中无平行线求线段的比时,有时也需要做平行线,可将一条直线上的两条线段的比转化到另一条直线中来求.
【针对训练】
如图所示,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD:AB=3∶4,AE=6,则AC等于( )
A.3
B.4
C.6
D.8
二、课堂小结
基本事实
推论
内容
两条直线被一组平行线所截,截得的对应线段____.如图,l1
∥
l2∥
l3,则
①平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段______;②平行与三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边_______.
图例
1..已知线段a,b,c,求作第四比例线段x,下列作图正确的是( )
2..如图所示,直线l1∥l2∥l3,下列比例式中成立的是(
)
A.=
B.=
C.=
D.=
3.如图,路灯距离地面8m,身高1.6m的小明站在距离灯的底部(点O)20m的A处,则小明的影子AM长为________m.
4.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,DE=4,BC=6,AD=5.求DC与AE的长.
当堂检测参考答案:
D
2.D
3.5
4.∵DE∥BC,∴=.
又DE=4,BC=6,AD=5,
∴=.∴AC=.
∴DC=AC-AD=.
∵DE∥BC,∴=.
∴∠DBC=∠EDB.
∵BD平分∠ABC,∴∠EBD=∠DBC.
∴∠EBD=∠EDB.
∴DE=BE=4,==.∴AE=8.
自主学习
合作探究
当堂检测
平行线分线段成比例
学习目标:
学习并掌握平行线分线段成比例定理及其推论并学会运用.
2.能够运用平行线分线段成比例定理及推论解决问题.
学习重点:平行线分线段成比例定理及其推论.
学习难点:平行线分线段成比例定理及其推论的运用.
新知预习
问题1:如图①,小方格的边长均为1,直线l1∥l2∥l3,分别交直线m,n于点A1,A2,A3,B1,B2,B3.
利用勾股定理计算:
计算:
图①
图②
这些比值有什么关系?你有什么发现?
问题2:将l2向下平移到如图②的位置,直线m,n与l2的交点分别为A2,B2,你在上题中发现的规律还成立吗?如果将l2平移到其他位置呢?
【猜想】在平面上任意作三条平行线,用它们截两条直线,所截得的线段成比例吗?
【归纳】
二、自学自测
1.如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,=,则EC的长是( )
第1题图
第2题图
A.4.5
B.8
C.10.5
D.14
2.如图,直线AB∥CD∥EF,若AC=3,CE=4,则的值是( )
A.
B.
C.
D.
三、我的疑惑
_____________________________________________________________________________
要点探究
探究点1:平行线分线段成比例定理(基本事实)
例1:如图,直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3,已知EF∶DF=5∶8,AC=24.
求AB的长;
解:∵l1∥l2∥l3,EF∶DF=5∶8,AC=24,
∴==_____,=_____.∴BC=_____.∴AB=AC-BC=_____
(2)当AD=4,BE=1时,求CF的长.
解:∵l1∥l2,∴==_____.∴=_____.
∴OB=_____.∴OC=BC-OB=_____.
∵l2∥l3,∴==_____.∴=_____∴CF=_____.
【归纳总结】利用平行线分线段成比例求线段长的方法:先确定图中的平行线,由此联想到线段之间的比例关系,结合待求线段和已知线段写出一个含有它们的比例关系式,构造出方程,解方程求出待求线段长.
【针对训练】
如图,直线l1∥l2∥l3,直线AC分别交这三条直线于点A,B,C,直线DF分别交这三条直线于点D,E,F,若AB=3,DE=,EF=4,求BC的长.
探究点2:平行线分线段成比例的推论
【做一做】如图,直线,分别交直线m,n于A1,A2,A3,B1,B2,B3.
图中有哪些成比例线段?
(2)
如果把图1中A1A3,B1B3.两条直线相交,交点刚落到上l1
,如图3所得的对应线段的比
________,依据是_____________________________.
(3)如果把图1中A1A3,B1B3.两条直线相交,交点刚落到上
l2,如图4所得的对应线段的比_________,依据是______________________________________.
【归纳】推论:
内容
字母表示
图例
推论1
平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
EF∥BC
推论2
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.
为了便于记忆,平行中的等比例式可使用一些简单的形象化的语言:
例2:如图所示,在△ABC中,E,F,分别是AB和AC的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
解:
∵EF∥BC,
∴________________.
∵AE
=
7,
EB
=
5
,
FC
=
4.
∴AF=_________________.
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
解:
∵EF∥BC,
∴________________.
∵AB
=
10
,
AE
=
6
,
AF
=
5.
∴________________.
∴FC=AC
–
AF
=________________.
例3:如图,在△ABC的边AB上取一点D,在AC上取一点E,使得AD=AE,直线DE和BC的延长线相交于P,求证:=.
【思路提示】过点C作DE的平行线.
证明:
【归纳总结】在由平行线推出成比例线段的比例式时,要注意它们的相互位置关系,比例式不能写错,要把对应的线段写在对应的位置上.当题中无平行线求线段的比时,有时也需要做平行线,可将一条直线上的两条线段的比转化到另一条直线中来求.
【针对训练】
如图所示,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD:AB=3∶4,AE=6,则AC等于( )
A.3
B.4
C.6
D.8
二、课堂小结
基本事实
推论
内容
两条直线被一组平行线所截,截得的对应线段____.如图,l1
∥
l2∥
l3,则
①平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段______;②平行与三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边_______.
图例
1..已知线段a,b,c,求作第四比例线段x,下列作图正确的是( )
2..如图所示,直线l1∥l2∥l3,下列比例式中成立的是(
)
A.=
B.=
C.=
D.=
3.如图,路灯距离地面8m,身高1.6m的小明站在距离灯的底部(点O)20m的A处,则小明的影子AM长为________m.
4.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥BC交AB于点E,DE=4,BC=6,AD=5.求DC与AE的长.
当堂检测参考答案:
D
2.D
3.5
4.∵DE∥BC,∴=.
又DE=4,BC=6,AD=5,
∴=.∴AC=.
∴DC=AC-AD=.
∵DE∥BC,∴=.
∴∠DBC=∠EDB.
∵BD平分∠ABC,∴∠EBD=∠DBC.
∴∠EBD=∠EDB.
∴DE=BE=4,==.∴AE=8.
自主学习
合作探究
当堂检测
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
