2017九年级数学上册25.3相似三角形导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.3相似三角形导学案(新版)冀教版 |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 18:12:08 | ||
图片预览

文档简介
25.3
相似三角形
学习目标:
理解并掌握相似三角形的定义,并能够根据其解决简单问题.
2.掌握运用平行线判定两个三角形相似的方法.
学习重点:相似三角形的定义.
学习难点:用平行线判定两个三角形相似的方法.
知识链接
什么叫全等三角形?
答:______________________________________.
全等三角形有哪些性质?
答:_____________________________________.
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边有什么关系?
二、新知预习
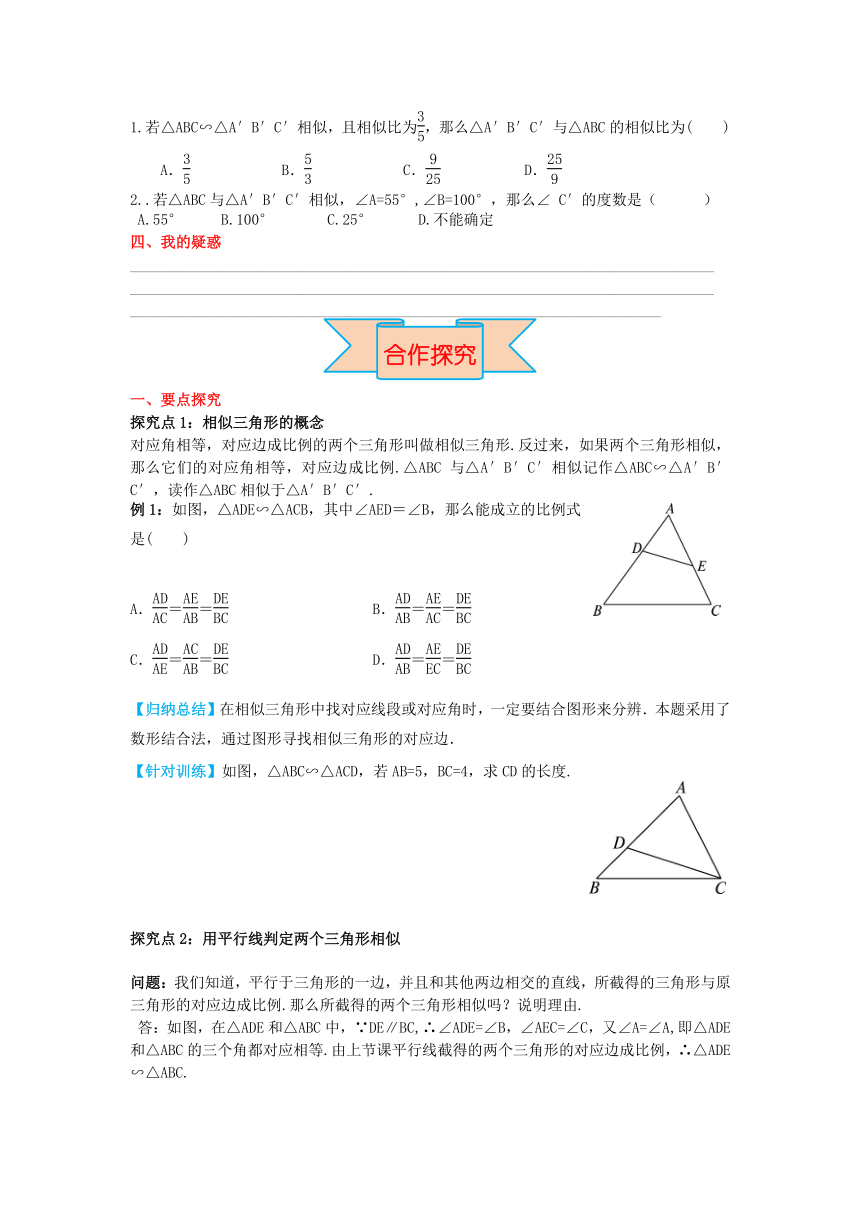
3.下面的图形有什么相同点和不同点
图(1)中各角的度数分别为______、______、______.
图(1)中各边的长度分别为______、______、______.图(4)中各角的度数分别为______、______、______.
图(4)中各边的长度分别为______、______、______.
图(2)中各角的度数分别为______、______、______.
图(2)中各边的长度分别为______、______、______.图(3)中各角的度数分别为______、______、______.
图(5)中各边的长度分别为______、______、______.
图(3)中各角的度数分别为______、______、______.
图(3)中各边的长度分别为______、______、______.图(6)中各角的度数分别为______、______、______.
图(6)中各边的长度分别为______、______、______.
【归纳】
对应角_______、对应边______的两个三角形叫做相似三角形.相似三角形的对应边的比叫做他们的相似比.
自学自测
1.若△ABC∽△A′B′C′相似,且相似比为,那么△A′B′C′与△ABC的相似比为( )
A.
B.
C.
D.
2..若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
______________________________________________________________________
要点探究
探究点1:相似三角形的概念
对应角相等,对应边成比例的两个三角形叫做相似三角形.反过来,如果两个三角形相似,那么它们的对应角相等,对应边成比例.△ABC与△A′B′C′相似记作△ABC∽△A′B′C′,读作△ABC相似于△A′B′C′.
例1:如图,△ADE∽△ACB,其中∠AED=∠B,那么能成立的比例式是( )
A.==
B.==
C.==
D.==
【归纳总结】在相似三角形中找对应线段或对应角时,一定要结合图形来分辨.本题采用了数形结合法,通过图形寻找相似三角形的对应边.
【针对训练】如图,△ABC∽△ACD,若AB=5,BC=4,求CD的长度.
探究点2:用平行线判定两个三角形相似
问题:我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.那么所截得的两个三角形相似吗?说明理由.
答:如图,在△ADE和△ABC中,∵DE∥BC,∴∠ADE=∠B,∠AEC=∠C,又∠A=∠A,即△ADE和△ABC的三个角都对应相等.由上节课平行线截得的两个三角形的对应边成比例,∴△ADE∽△ABC.
【归纳】平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
例2:如图所示,已知DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
解:方法一:因为DE∥BC,所以_____________,_____________,所以△ADE∽△ABC,
所以_____________,即_____________,所以BC=_______cm.又因为DF∥AC,
所以四边形DFCE是平行四边形,所以FC=DE=___cm,所以BF=BC-FC=___(cm).
方法二:因为DE∥BC,所以_____________.又因为DF∥AC,所以_____________,
所以△ADE∽△DBF,
所以__________,即___________所以BF=________cm.
【归纳总结】求线段的长,常通过找三角形相似得到成比例线段而求得,因此选择哪两个三角形就成了解题的关键,这就需要通过已知的线段和所求的线段分析得到.
【针对训练】
如图,DE∥BC,若AE=3,EC=5,DE=3.6,则BC的长为__________.
二、课堂小结
相似三角形
内容
基本图形
概念
对应角_______、对应边______的两个三角形叫做相似三角形.
用平行线判定两个三角形相似
①“A”字型:如图1,DE∥BC;②“X”字型:如图2,DE∥BC;
解题策略
题目中无图,题干中也未给出对应点,说明两三角形相似时,要注意分情况讨论.
1.如图,点P是△ABC的边AB上的一点,且满足△APC∽△ACB,则下列比例式:
①=;②=;③=;④=.
其中正确的是( )
A.①②
B.③④
C.①②③
D.②③④
2.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
已知△ABC中,AC=3,BC=4,AB=5,若△ABC∽△A1B1C1,且△A1B1C1的最大边长是15,求△A1B1C1的面积.
如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
当堂检测参考答案:
A
2.B
3.因为32+42=52,
所以△ABC是直角三角形,且∠C=90°.
因为△ABC∽△A1B1C1,
所以△A1B1C1也是直角三角形,A1C1与B1C1垂直,A1B1=15,==,
所以A1C1=·AC=9,B1C1=·BC=12.
所以S△A1B1C1=A1C1·B1C1=×9×12=54.
4.(1)∵四边形ABCD是平行四边形,
∴AQ∥BC,∴△DQP∽△CBP.
(2)∵△DQP≌△CBP,
∴DP=CP=CD.
∵AB=CD=8,∴DP=4.
自主学习
合作探究
当堂检测
相似三角形
学习目标:
理解并掌握相似三角形的定义,并能够根据其解决简单问题.
2.掌握运用平行线判定两个三角形相似的方法.
学习重点:相似三角形的定义.
学习难点:用平行线判定两个三角形相似的方法.
知识链接
什么叫全等三角形?
答:______________________________________.
全等三角形有哪些性质?
答:_____________________________________.
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边有什么关系?
二、新知预习
3.下面的图形有什么相同点和不同点
图(1)中各角的度数分别为______、______、______.
图(1)中各边的长度分别为______、______、______.图(4)中各角的度数分别为______、______、______.
图(4)中各边的长度分别为______、______、______.
图(2)中各角的度数分别为______、______、______.
图(2)中各边的长度分别为______、______、______.图(3)中各角的度数分别为______、______、______.
图(5)中各边的长度分别为______、______、______.
图(3)中各角的度数分别为______、______、______.
图(3)中各边的长度分别为______、______、______.图(6)中各角的度数分别为______、______、______.
图(6)中各边的长度分别为______、______、______.
【归纳】
对应角_______、对应边______的两个三角形叫做相似三角形.相似三角形的对应边的比叫做他们的相似比.
自学自测
1.若△ABC∽△A′B′C′相似,且相似比为,那么△A′B′C′与△ABC的相似比为( )
A.
B.
C.
D.
2..若△ABC与△A′B′C′相似,∠A=55°,∠B=100°,那么∠
C′的度数是(
)
A.55°
B.100°
C.25°
D.不能确定
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
______________________________________________________________________
要点探究
探究点1:相似三角形的概念
对应角相等,对应边成比例的两个三角形叫做相似三角形.反过来,如果两个三角形相似,那么它们的对应角相等,对应边成比例.△ABC与△A′B′C′相似记作△ABC∽△A′B′C′,读作△ABC相似于△A′B′C′.
例1:如图,△ADE∽△ACB,其中∠AED=∠B,那么能成立的比例式是( )
A.==
B.==
C.==
D.==
【归纳总结】在相似三角形中找对应线段或对应角时,一定要结合图形来分辨.本题采用了数形结合法,通过图形寻找相似三角形的对应边.
【针对训练】如图,△ABC∽△ACD,若AB=5,BC=4,求CD的长度.
探究点2:用平行线判定两个三角形相似
问题:我们知道,平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例.那么所截得的两个三角形相似吗?说明理由.
答:如图,在△ADE和△ABC中,∵DE∥BC,∴∠ADE=∠B,∠AEC=∠C,又∠A=∠A,即△ADE和△ABC的三个角都对应相等.由上节课平行线截得的两个三角形的对应边成比例,∴△ADE∽△ABC.
【归纳】平行于三角形一边的直线和其他两边(或它们的延长线)相交,所截得的三角形与原三角形相似.
例2:如图所示,已知DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,求线段BF的长.
解:方法一:因为DE∥BC,所以_____________,_____________,所以△ADE∽△ABC,
所以_____________,即_____________,所以BC=_______cm.又因为DF∥AC,
所以四边形DFCE是平行四边形,所以FC=DE=___cm,所以BF=BC-FC=___(cm).
方法二:因为DE∥BC,所以_____________.又因为DF∥AC,所以_____________,
所以△ADE∽△DBF,
所以__________,即___________所以BF=________cm.
【归纳总结】求线段的长,常通过找三角形相似得到成比例线段而求得,因此选择哪两个三角形就成了解题的关键,这就需要通过已知的线段和所求的线段分析得到.
【针对训练】
如图,DE∥BC,若AE=3,EC=5,DE=3.6,则BC的长为__________.
二、课堂小结
相似三角形
内容
基本图形
概念
对应角_______、对应边______的两个三角形叫做相似三角形.
用平行线判定两个三角形相似
①“A”字型:如图1,DE∥BC;②“X”字型:如图2,DE∥BC;
解题策略
题目中无图,题干中也未给出对应点,说明两三角形相似时,要注意分情况讨论.
1.如图,点P是△ABC的边AB上的一点,且满足△APC∽△ACB,则下列比例式:
①=;②=;③=;④=.
其中正确的是( )
A.①②
B.③④
C.①②③
D.②③④
2.如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有( )
A.1个
B.2个
C.3个
D.4个
已知△ABC中,AC=3,BC=4,AB=5,若△ABC∽△A1B1C1,且△A1B1C1的最大边长是15,求△A1B1C1的面积.
如图,点P在平行四边形ABCD的CD边上,连接BP并延长与AD的延长线交于点Q.
(1)求证:△DQP∽△CBP;
(2)当△DQP≌△CBP,且AB=8时,求DP的长.
当堂检测参考答案:
A
2.B
3.因为32+42=52,
所以△ABC是直角三角形,且∠C=90°.
因为△ABC∽△A1B1C1,
所以△A1B1C1也是直角三角形,A1C1与B1C1垂直,A1B1=15,==,
所以A1C1=·AC=9,B1C1=·BC=12.
所以S△A1B1C1=A1C1·B1C1=×9×12=54.
4.(1)∵四边形ABCD是平行四边形,
∴AQ∥BC,∴△DQP∽△CBP.
(2)∵△DQP≌△CBP,
∴DP=CP=CD.
∵AB=CD=8,∴DP=4.
自主学习
合作探究
当堂检测
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
