2017九年级数学上册25.4第3课时利用三边关系判定两三角形相似导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.4第3课时利用三边关系判定两三角形相似导学案(新版)冀教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 333.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 00:00:00 | ||
图片预览

文档简介
25.4
相似三角形的判定
第3课时
利用三边关系判定两三角形相似
学习目标:
学习并掌握相似三角形判定定理3.
学会相似三角形的判定定理3的应用.
学习重点:准确找出相似三角形的对应边.
学习难点:掌握相似三角形判定定理3及其应用.
知识链接
类比全等三角形的判定方法,结合学过的证明两个三角形相似的方法,填一填
两角
两边+夹角
三边
直角三角形
全等
AAS或ASA
SAS
SSS
HL
相似
两角对应相等
两边对应成比例,夹角相等
猜想1:三边_________?
猜想2:直角边、斜边__________
新知预习
2.如图,在半透明的纸上画一个△ABC,使AB=1.5cm,AC=2.5cm,BC=2cm,在画一个△A'B'C',使得A'B'=3cm,A'C'=5cm,B'C'=4cm.
比较△ABC和△A'B'C'各个角,它们对应相等吗?这两个三角相似吗?
答:________________________________________.
我们可以初步确定猜想:三边对应成比例的两个三角形________.
三、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:利用三边的关系判定相似三角形
【证明猜想1】已知在△ABC和△A1B1C1中,.求证:△ABC∽△A1B1C1.
补全下面证明过程:
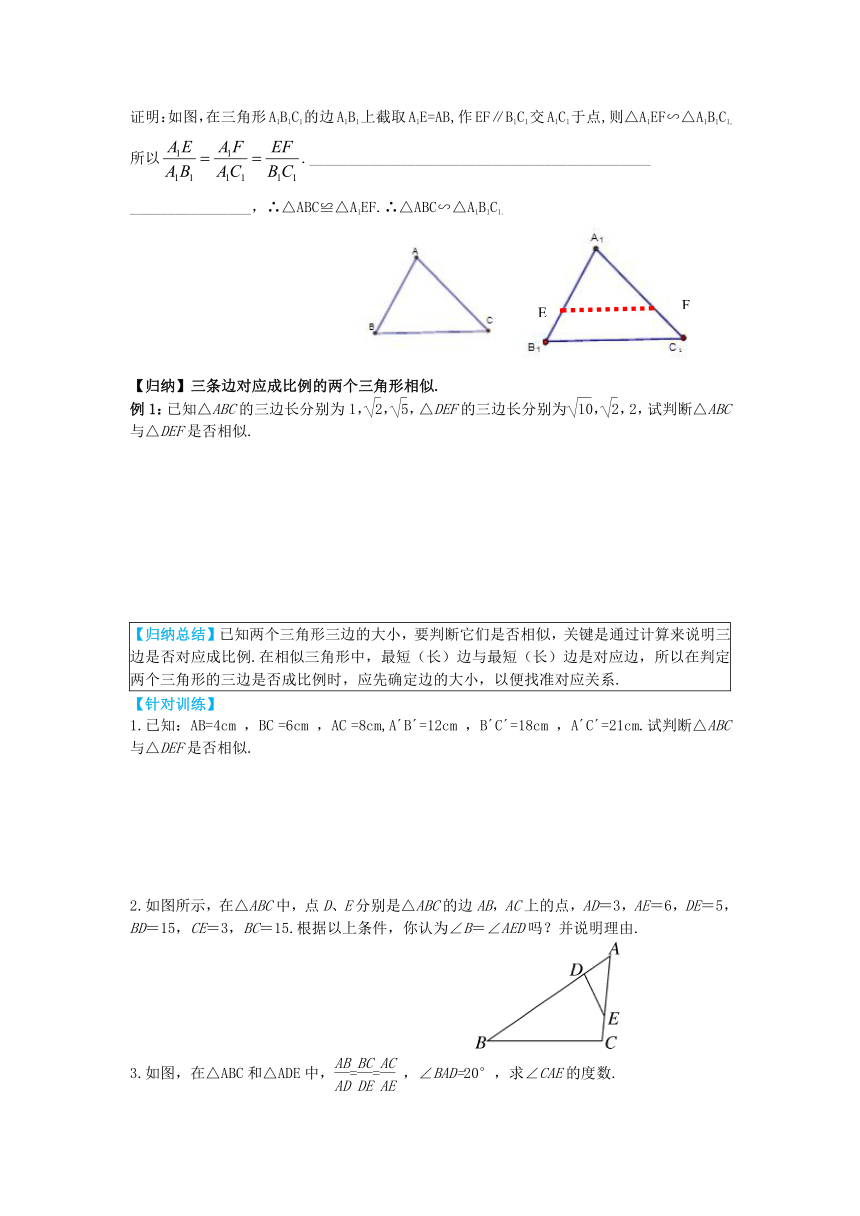
证明:如图,在三角形A1B1C1的边A1B1上截取A1E=AB,作EF∥B1C1交A1C1于点,则△A1EF∽△A1B1C1,所以._____________________________________________
________________,∴△ABC≌△A1EF.∴△ABC∽△A1B1C1.
【归纳】三条边对应成比例的两个三角形相似.
例1:已知△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,试判断△ABC与△DEF是否相似.
【归纳总结】已知两个三角形三边的大小,要判断它们是否相似,关键是通过计算来说明三边是否对应成比例.在相似三角形中,最短(长)边与最短(长)边是对应边,所以在判定两个三角形的三边是否成比例时,应先确定边的大小,以便找准对应关系.
【针对训练】
1.已知:AB=4cm
,BC
=6cm
,AC
=8cm,A B =12cm
,B C =18cm
,A C =21cm.试判断△ABC与△DEF是否相似.
2.如图所示,在△ABC中,点D、E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
3.如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
探究点2:利用边判定直角三角形相似
【证明猜想2】已知,如图,在Rt△ABC与Rt△A′B′C′中,∠B=∠B′=90°,.求证:Rt△ABC∽Rt△A′B′C′.
思路分析:结合勾股定理,利用三边对应成比例证明,可设=k,则只需证=k.
证明:
【归纳】直角边和斜边对应成比例的两个直角三角形相似.
问题:如图所示,在单位长度为1的网格中,相似的三角形有哪些?
【归纳总结】(1)各个图形中的三角形均为格点三角形,可以根据勾股定理求出各边的长,然后根据三角形三边的长度是否成比例来判断两个三角形是否相似;(2)判断三边是否成比例,可以将三角形的三边长按大小顺序排列,然后分别计算他们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
二、课堂小结
判定3
三条边对应成比例的两个三角形相似.
直角三角形相似的基本类型
图1中,_____=_____,△ACB∽△CDB._____=_____,△ACB∽△ADC._____=_____,△CDB△ADC.图2中,∠1=∠2,则____=_____,△AEB∽△CED.图3中,_____=_____,△AEB∽△DEC.
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当DEF的另一边长
是下面哪一组时,这两个三角形相似(
)
A.2cm
3cm
B.4cm
5cm
C.5cm
6cm
D.6cm
7cm
一三角形三边长是3、5/7,另一个与它相似的三角形的最长边是21,则其他两边之和是
________.
如图所示的两个三角形相似吗?请证明.
4.如图甲,小正方形的边长均为1,则乙图中的三角形(阴影部分)与△ABC相似的是哪一个图形?
当堂检测参考答案:
1.C
2.21
3.相似.证明略.
4.由甲图可知AC==,BC=2,AB==.
同理,图①中,三角形的三边长分别为1,,2;
同理,图②中,三角形的三边长分别为1,,;
同理,图③中,三角形的三边长分别为,,3;
同理,图④中,三角形的三边长分别为2,,.
∵===,
∴图②中的三角形与△ABC相似.
自主学习
合作探究
E
F
当堂检测
相似三角形的判定
第3课时
利用三边关系判定两三角形相似
学习目标:
学习并掌握相似三角形判定定理3.
学会相似三角形的判定定理3的应用.
学习重点:准确找出相似三角形的对应边.
学习难点:掌握相似三角形判定定理3及其应用.
知识链接
类比全等三角形的判定方法,结合学过的证明两个三角形相似的方法,填一填
两角
两边+夹角
三边
直角三角形
全等
AAS或ASA
SAS
SSS
HL
相似
两角对应相等
两边对应成比例,夹角相等
猜想1:三边_________?
猜想2:直角边、斜边__________
新知预习
2.如图,在半透明的纸上画一个△ABC,使AB=1.5cm,AC=2.5cm,BC=2cm,在画一个△A'B'C',使得A'B'=3cm,A'C'=5cm,B'C'=4cm.
比较△ABC和△A'B'C'各个角,它们对应相等吗?这两个三角相似吗?
答:________________________________________.
我们可以初步确定猜想:三边对应成比例的两个三角形________.
三、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:利用三边的关系判定相似三角形
【证明猜想1】已知在△ABC和△A1B1C1中,.求证:△ABC∽△A1B1C1.
补全下面证明过程:
证明:如图,在三角形A1B1C1的边A1B1上截取A1E=AB,作EF∥B1C1交A1C1于点,则△A1EF∽△A1B1C1,所以._____________________________________________
________________,∴△ABC≌△A1EF.∴△ABC∽△A1B1C1.
【归纳】三条边对应成比例的两个三角形相似.
例1:已知△ABC的三边长分别为1,,,△DEF的三边长分别为,,2,试判断△ABC与△DEF是否相似.
【归纳总结】已知两个三角形三边的大小,要判断它们是否相似,关键是通过计算来说明三边是否对应成比例.在相似三角形中,最短(长)边与最短(长)边是对应边,所以在判定两个三角形的三边是否成比例时,应先确定边的大小,以便找准对应关系.
【针对训练】
1.已知:AB=4cm
,BC
=6cm
,AC
=8cm,A B =12cm
,B C =18cm
,A C =21cm.试判断△ABC与△DEF是否相似.
2.如图所示,在△ABC中,点D、E分别是△ABC的边AB,AC上的点,AD=3,AE=6,DE=5,BD=15,CE=3,BC=15.根据以上条件,你认为∠B=∠AED吗?并说明理由.
3.如图,在△ABC和△ADE中,==
,∠BAD=20°,求∠CAE的度数.
探究点2:利用边判定直角三角形相似
【证明猜想2】已知,如图,在Rt△ABC与Rt△A′B′C′中,∠B=∠B′=90°,.求证:Rt△ABC∽Rt△A′B′C′.
思路分析:结合勾股定理,利用三边对应成比例证明,可设=k,则只需证=k.
证明:
【归纳】直角边和斜边对应成比例的两个直角三角形相似.
问题:如图所示,在单位长度为1的网格中,相似的三角形有哪些?
【归纳总结】(1)各个图形中的三角形均为格点三角形,可以根据勾股定理求出各边的长,然后根据三角形三边的长度是否成比例来判断两个三角形是否相似;(2)判断三边是否成比例,可以将三角形的三边长按大小顺序排列,然后分别计算他们对应边的比,最后由比值是否相等来确定两个三角形是否相似.
二、课堂小结
判定3
三条边对应成比例的两个三角形相似.
直角三角形相似的基本类型
图1中,_____=_____,△ACB∽△CDB._____=_____,△ACB∽△ADC._____=_____,△CDB△ADC.图2中,∠1=∠2,则____=_____,△AEB∽△CED.图3中,_____=_____,△AEB∽△DEC.
已知△ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当DEF的另一边长
是下面哪一组时,这两个三角形相似(
)
A.2cm
3cm
B.4cm
5cm
C.5cm
6cm
D.6cm
7cm
一三角形三边长是3、5/7,另一个与它相似的三角形的最长边是21,则其他两边之和是
________.
如图所示的两个三角形相似吗?请证明.
4.如图甲,小正方形的边长均为1,则乙图中的三角形(阴影部分)与△ABC相似的是哪一个图形?
当堂检测参考答案:
1.C
2.21
3.相似.证明略.
4.由甲图可知AC==,BC=2,AB==.
同理,图①中,三角形的三边长分别为1,,2;
同理,图②中,三角形的三边长分别为1,,;
同理,图③中,三角形的三边长分别为,,3;
同理,图④中,三角形的三边长分别为2,,.
∵===,
∴图②中的三角形与△ABC相似.
自主学习
合作探究
E
F
当堂检测
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
