2017九年级数学上册25.6相似三角形的应用导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.6相似三角形的应用导学案(新版)冀教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 18:19:26 | ||
图片预览


文档简介
25.6
相似三角形的应用
学习目标:
理解并掌握运用相似三角形测量物体高度和宽度的方法.
学习重点:运用相似三角形测量.
学习难点:相似三角形的性质和判定的综合应用.
知识链接
如何判定两个三角形相似?
答:________________________________________.
相似三角形的性质有哪些?
答:________________________________________.
我们学过哪些方法测量物体的高度和宽度?
答:____________________________________.
新知预习
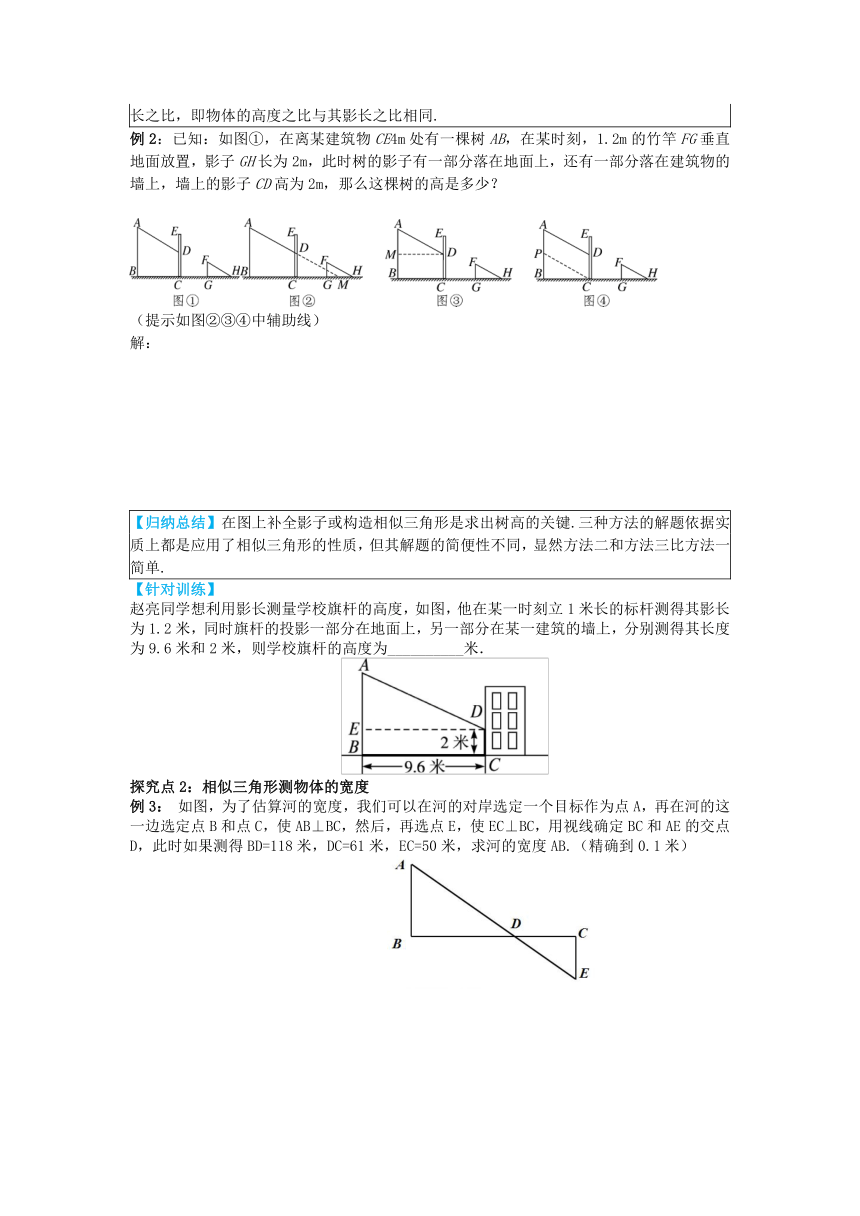
如图,有些空心圆柱形机械零件的内径是不能直接测量的,往往需要使用教程卡钳进行测量,图中为一个零件的剖面图,它的外经为a,内径AB未知,现用交叉卡钳去测量,若,CD=b,则这个零件的内径为多少?零件的壁厚x又是多少?(用含有a、b、m的代数式表示)
解:∵,∠_____=∠_____.
∴△______∽△______.
∴______
又∵CD=b,∴AB=_____,x=_______.
故这个零件的内径为_________零件的壁厚x是______.
如图,在学校操场上,高高耸立的旗杆上悬挂着五星红旗.如何测量学校操场上旗杆的高度呢?某同学给出了一种测量方法,你能根据其设计出其他的方案吗?
解:
三、自学自测
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=6m,则池塘的宽DE为( )
A.25m
B.30m
C.36m
D.40m
2.如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )
A.6.4米
B.8米
C.9.6米
D.11.2米
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_______________________________________________________________________
要点探究
探究点1:相似三角形测物体的高度
例1:如图所示,身高为1.6m的某同学想测量学校旗杆的高度,当他站在C处时,正好站在旗杆影子的顶端处,已测得该同学在地面上的影长为2m,旗杆在地面上的影长为8m,那么旗杆的高度是多少呢?
【归纳总结】同一时刻,对于都垂直于地面的两个物体来说,它们的高度之比等于它们的影长之比,即物体的高度之比与其影长之比相同.
例2:已知:如图①,在离某建筑物CE4m处有一棵树AB,在某时刻,1.2m的竹竿FG垂直地面放置,影子GH长为2m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2m,那么这棵树的高是多少?
(提示如图②③④中辅助线)
解:
【归纳总结】在图上补全影子或构造相似三角形是求出树高的关键.三种方法的解题依据实质上都是应用了相似三角形的性质,但其解题的简便性不同,显然方法二和方法三比方法一简单.
【针对训练】
赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为__________米.
探究点2:相似三角形测物体的宽度
例3:
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=118米,DC=61米,EC=50米,求河的宽度AB.(精确到0.1米)
【归纳总结】测量不能直接到达两点间的距离,常构造相似三角形求解.
【针对训练】
如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m
B.25m
C.28m
D.30m
二、课堂小结
相似三角形的应用
基本图形
测量高度
测量宽度
1.如图,A,B两处被池塘隔开,为了测量A,B两处的距离,在AB外选一适当的点C,连结AC,BC,并分别取线段AC,BC的中点E,F,测得EF=20m,则AB=__________m.
2.如图所示,CD是一个平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D.若AC=3,CE=4,ED=8,则BD=________.
3.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
4.一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图(1),乙设计方案如图(2).你认为哪位同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
(1) (2)
当堂检测参考答案:
1.40
2.6
3.过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
所以∠ABF=∠EFD=∠CDF=90°,
所以AB∥EF∥CD,所以∠EMA=∠CNA.
因为∠EAM=∠CAN,
所以△AEM∽△ACN,所以=.
因为AB=1.6m,EF=2m,BD=27m,FD=24m,
所以=,所以CN=3.6(m),
所以CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
4.由AB=1.5m,S△ABC=1.5m2,可得BC=2m.
(1) (2)
由图(1),若设甲设计的正方形桌面边长为xm.
由DE∥AB,得Rt△CDE∽Rt△CBA,
所以=,
即=,
所以x=m.
由图(2),过点B作Rt△ABC斜边上的高BH交DE于P,交AC于H.
由AB=1.5,BC=2,
得AC===2.5
(m).
由AC·BH=AB·BC,可得
BH===1.2
(m).
设乙设计的桌面的边长为ym.
因为DE∥AC,Rt△BDE∽Rt△BAC,
所以=.
即=,解得y=m.
因为=>,所以x2>y2.
故甲同学设计的方案较好.
自主学习
合作探究
当堂检测
相似三角形的应用
学习目标:
理解并掌握运用相似三角形测量物体高度和宽度的方法.
学习重点:运用相似三角形测量.
学习难点:相似三角形的性质和判定的综合应用.
知识链接
如何判定两个三角形相似?
答:________________________________________.
相似三角形的性质有哪些?
答:________________________________________.
我们学过哪些方法测量物体的高度和宽度?
答:____________________________________.
新知预习
如图,有些空心圆柱形机械零件的内径是不能直接测量的,往往需要使用教程卡钳进行测量,图中为一个零件的剖面图,它的外经为a,内径AB未知,现用交叉卡钳去测量,若,CD=b,则这个零件的内径为多少?零件的壁厚x又是多少?(用含有a、b、m的代数式表示)
解:∵,∠_____=∠_____.
∴△______∽△______.
∴______
又∵CD=b,∴AB=_____,x=_______.
故这个零件的内径为_________零件的壁厚x是______.
如图,在学校操场上,高高耸立的旗杆上悬挂着五星红旗.如何测量学校操场上旗杆的高度呢?某同学给出了一种测量方法,你能根据其设计出其他的方案吗?
解:
三、自学自测
1.如图,为了测量一池塘的宽DE,在岸边找到一点C,测得CD=30m,在DC的延长线上找一点A,测得AC=5m,过点A作AB∥DE交EC的延长线于B,测出AB=6m,则池塘的宽DE为( )
A.25m
B.30m
C.36m
D.40m
2.如图,小亮同学在晚上由路灯A走向路灯B,当他走到点P时,发现他的身影顶部正好接触路灯B的底部,这时他离路灯A25米,离路灯B5米,如果小亮的身高为1.6米,那么路灯高度为( )
A.6.4米
B.8米
C.9.6米
D.11.2米
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_______________________________________________________________________
要点探究
探究点1:相似三角形测物体的高度
例1:如图所示,身高为1.6m的某同学想测量学校旗杆的高度,当他站在C处时,正好站在旗杆影子的顶端处,已测得该同学在地面上的影长为2m,旗杆在地面上的影长为8m,那么旗杆的高度是多少呢?
【归纳总结】同一时刻,对于都垂直于地面的两个物体来说,它们的高度之比等于它们的影长之比,即物体的高度之比与其影长之比相同.
例2:已知:如图①,在离某建筑物CE4m处有一棵树AB,在某时刻,1.2m的竹竿FG垂直地面放置,影子GH长为2m,此时树的影子有一部分落在地面上,还有一部分落在建筑物的墙上,墙上的影子CD高为2m,那么这棵树的高是多少?
(提示如图②③④中辅助线)
解:
【归纳总结】在图上补全影子或构造相似三角形是求出树高的关键.三种方法的解题依据实质上都是应用了相似三角形的性质,但其解题的简便性不同,显然方法二和方法三比方法一简单.
【针对训练】
赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为__________米.
探究点2:相似三角形测物体的宽度
例3:
如图,为了估算河的宽度,我们可以在河的对岸选定一个目标作为点A,再在河的这一边选定点B和点C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D,此时如果测得BD=118米,DC=61米,EC=50米,求河的宽度AB.(精确到0.1米)
【归纳总结】测量不能直接到达两点间的距离,常构造相似三角形求解.
【针对训练】
如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是( )
A.24m
B.25m
C.28m
D.30m
二、课堂小结
相似三角形的应用
基本图形
测量高度
测量宽度
1.如图,A,B两处被池塘隔开,为了测量A,B两处的距离,在AB外选一适当的点C,连结AC,BC,并分别取线段AC,BC的中点E,F,测得EF=20m,则AB=__________m.
2.如图所示,CD是一个平面镜,光线从A点射出经CD上的E点反射后照射到B点,设入射角为α(入射角等于反射角),AC⊥CD,BD⊥CD,垂足分别为C,D.若AC=3,CE=4,ED=8,则BD=________.
3.如图,小明为了测量一棵树CD的高度,他在距树24m处立了一根高为2m的标杆EF,然后小明前后调整自己的位置,当他与树相距27m的时候,他的眼睛、标杆的顶端和树的顶端在同一条直线上.已知小明的眼高1.6m,求树的高度.
4.一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学设计加工方案,甲设计方案如图(1),乙设计方案如图(2).你认为哪位同学设计的方案较好?试说明理由(加工损耗忽略不计,计算结果可保留分数).
(1) (2)
当堂检测参考答案:
1.40
2.6
3.过点A作AN∥BD交CD于N,交EF于M,因为人、标杆、树都垂直于地面,
所以∠ABF=∠EFD=∠CDF=90°,
所以AB∥EF∥CD,所以∠EMA=∠CNA.
因为∠EAM=∠CAN,
所以△AEM∽△ACN,所以=.
因为AB=1.6m,EF=2m,BD=27m,FD=24m,
所以=,所以CN=3.6(m),
所以CD=3.6+1.6=5.2(m).
故树的高度为5.2m.
4.由AB=1.5m,S△ABC=1.5m2,可得BC=2m.
(1) (2)
由图(1),若设甲设计的正方形桌面边长为xm.
由DE∥AB,得Rt△CDE∽Rt△CBA,
所以=,
即=,
所以x=m.
由图(2),过点B作Rt△ABC斜边上的高BH交DE于P,交AC于H.
由AB=1.5,BC=2,
得AC===2.5
(m).
由AC·BH=AB·BC,可得
BH===1.2
(m).
设乙设计的桌面的边长为ym.
因为DE∥AC,Rt△BDE∽Rt△BAC,
所以=.
即=,解得y=m.
因为=>,所以x2>y2.
故甲同学设计的方案较好.
自主学习
合作探究
当堂检测
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
