2017九年级数学上册25.7第1课时相似多边形导学案(新版)冀教版
文档属性
| 名称 | 2017九年级数学上册25.7第1课时相似多边形导学案(新版)冀教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 764.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 00:00:00 | ||
图片预览

文档简介
25.7
相似多边形和图形的位似
第1课时
相似多边形
学习目标:
理解相似图形的定义并能判断两图形是否相似.
学习并掌握相似多边形的性质与判定方法.
学习重点:判断两图形是否相似.
学习难点:相似多边形的性质与判定方法.
知识链接
有全等的多边形吗?若有,请你在下面的网格图中画出一组全等的多边形.
2.相似三角形的性质有哪些?
答:________________________________________.
新知预习
3.观察下面的几组图形,讨论它们的共同点.
像这样形状_________的图形称为相似图形.
4.如图,在上下两行图形中,把你认为是相似的图形用线连接起来.
一般地,如果两个多边形的对应角相等,对应边成比例,那么这两个多边形就叫做相似多边形.
三、自学自测
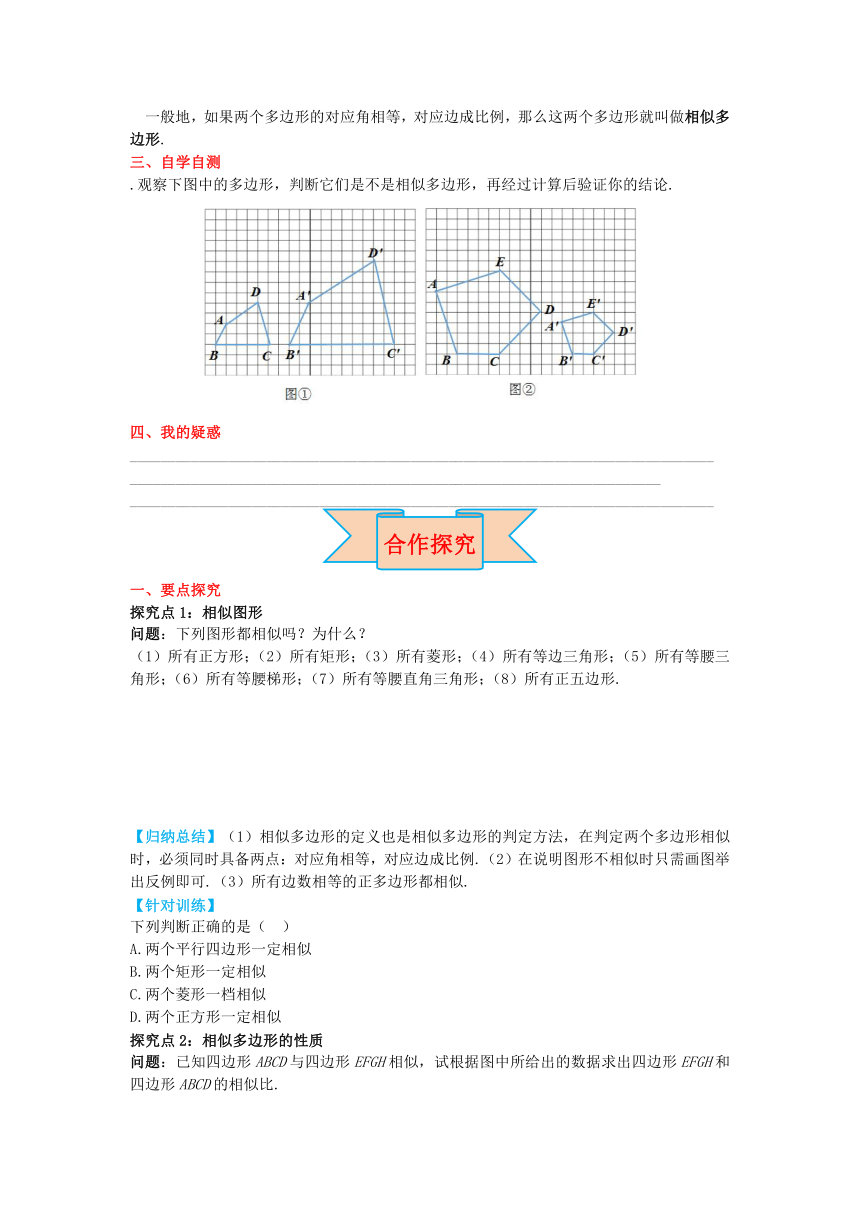
.观察下图中的多边形,判断它们是不是相似多边形,再经过计算后验证你的结论.
四、我的疑惑
_____________________________________________________________________________
______________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:相似图形
问题:下列图形都相似吗?为什么?
所有正方形;(2)所有矩形;(3)所有菱形;(4)所有等边三角形;(5)所有等腰三角形;(6)所有等腰梯形;(7)所有等腰直角三角形;(8)所有正五边形.
【归纳总结】(1)相似多边形的定义也是相似多边形的判定方法,在判定两个多边形相似时,必须同时具备两点:对应角相等,对应边成比例.(2)在说明图形不相似时只需画图举出反例即可.(3)所有边数相等的正多边形都相似.
【针对训练】
下列判断正确的是(
)
两个平行四边形一定相似
两个矩形一定相似
两个菱形一档相似
两个正方形一定相似
探究点2:相似多边形的性质
问题:已知四边形ABCD与四边形EFGH相似,试根据图中所给出的数据求出四边形EFGH和四边形ABCD的相似比.
【归纳总结】找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法.
【针对训练】
一个多边形的边长分别为2,3,4,5,6.另一个和它相似的多边形的最短边长为6,则其最长边为______.
探究点2:相似多边形的判断
问题:如图所示的两个矩形是否相似.
【针对训练】
根据下图所示,这两个多边形相似吗?说说你的理由.
二、课堂小结
相似多边形
内容
基本图形
概念
如果两个多边形的对应角_______,对应边成_____,那么这两个多边形就叫做相似多边形.
性质
的对应角_______,对应边成_____
1.下面每组图形中的两个图形是相似图形的是(
).
2.把下列菱形缩小为原来的一半.
3.如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
4.在AB=20m,AD=30m的矩形花坛ABCD的四周建筑小路.
如果四周的小路的宽均相等,如图①,那么小路四周所围成的矩形A′B′C′D′和矩形ABCD相似吗?请说明理由;、
(2)如果对应着的两条小路的宽均相等,如图②,试问小路的宽x与y的比值是多少时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似?
当堂检测参考答案:
C
2.
图略
3.因为四边形AEFD∽四边形EBCF,
所以=,
所以EF2=AD·BC=3×4=12,
所以EF==2.
因为四边形AEFD∽四边形EBCF,
所以AE:EB=AD:EF=3:2=:2.
4.(1)矩形A′B′C′D′和矩形ABCD不相似.理由如下:
假设两个矩形相似,不妨设小路宽为xm,
则=,解得x=0.
∵由题意可知,小路宽不可能为0,
∴矩形A′B′C′D′和矩形ABCD不相似;
(2)当x与y的比值为3:2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.理由如下:
若矩形A′B′C′D′和矩形ABCD相似,
则=,所以=.
∴当x与y的比值为3:2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
自主学习
合作探究
当堂检测
相似多边形和图形的位似
第1课时
相似多边形
学习目标:
理解相似图形的定义并能判断两图形是否相似.
学习并掌握相似多边形的性质与判定方法.
学习重点:判断两图形是否相似.
学习难点:相似多边形的性质与判定方法.
知识链接
有全等的多边形吗?若有,请你在下面的网格图中画出一组全等的多边形.
2.相似三角形的性质有哪些?
答:________________________________________.
新知预习
3.观察下面的几组图形,讨论它们的共同点.
像这样形状_________的图形称为相似图形.
4.如图,在上下两行图形中,把你认为是相似的图形用线连接起来.
一般地,如果两个多边形的对应角相等,对应边成比例,那么这两个多边形就叫做相似多边形.
三、自学自测
.观察下图中的多边形,判断它们是不是相似多边形,再经过计算后验证你的结论.
四、我的疑惑
_____________________________________________________________________________
______________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:相似图形
问题:下列图形都相似吗?为什么?
所有正方形;(2)所有矩形;(3)所有菱形;(4)所有等边三角形;(5)所有等腰三角形;(6)所有等腰梯形;(7)所有等腰直角三角形;(8)所有正五边形.
【归纳总结】(1)相似多边形的定义也是相似多边形的判定方法,在判定两个多边形相似时,必须同时具备两点:对应角相等,对应边成比例.(2)在说明图形不相似时只需画图举出反例即可.(3)所有边数相等的正多边形都相似.
【针对训练】
下列判断正确的是(
)
两个平行四边形一定相似
两个矩形一定相似
两个菱形一档相似
两个正方形一定相似
探究点2:相似多边形的性质
问题:已知四边形ABCD与四边形EFGH相似,试根据图中所给出的数据求出四边形EFGH和四边形ABCD的相似比.
【归纳总结】找准相似多边形的对应边是解决此类问题的关键,方法类似于找全等三角形对应边和对应角的方法.
【针对训练】
一个多边形的边长分别为2,3,4,5,6.另一个和它相似的多边形的最短边长为6,则其最长边为______.
探究点2:相似多边形的判断
问题:如图所示的两个矩形是否相似.
【针对训练】
根据下图所示,这两个多边形相似吗?说说你的理由.
二、课堂小结
相似多边形
内容
基本图形
概念
如果两个多边形的对应角_______,对应边成_____,那么这两个多边形就叫做相似多边形.
性质
的对应角_______,对应边成_____
1.下面每组图形中的两个图形是相似图形的是(
).
2.把下列菱形缩小为原来的一半.
3.如图所示,在四边形ABCD中,AD∥BC,EF∥BC,EF将四边形ABCD分成两个相似四边形AEFD和EBCF.若AD=3,BC=4,求AE:EB的值.
4.在AB=20m,AD=30m的矩形花坛ABCD的四周建筑小路.
如果四周的小路的宽均相等,如图①,那么小路四周所围成的矩形A′B′C′D′和矩形ABCD相似吗?请说明理由;、
(2)如果对应着的两条小路的宽均相等,如图②,试问小路的宽x与y的比值是多少时,能使小路四周所围成的矩形A′B′C′D′和矩形ABCD相似?
当堂检测参考答案:
C
2.
图略
3.因为四边形AEFD∽四边形EBCF,
所以=,
所以EF2=AD·BC=3×4=12,
所以EF==2.
因为四边形AEFD∽四边形EBCF,
所以AE:EB=AD:EF=3:2=:2.
4.(1)矩形A′B′C′D′和矩形ABCD不相似.理由如下:
假设两个矩形相似,不妨设小路宽为xm,
则=,解得x=0.
∵由题意可知,小路宽不可能为0,
∴矩形A′B′C′D′和矩形ABCD不相似;
(2)当x与y的比值为3:2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.理由如下:
若矩形A′B′C′D′和矩形ABCD相似,
则=,所以=.
∴当x与y的比值为3:2时,小路四周所围成的矩形A′B′C′D′和矩形ABCD相似.
自主学习
合作探究
当堂检测
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
