湖南省邵阳市邵阳县黄亭市镇中学2016-2017学年八年级数学(下)第三次月考试卷(含答案)
文档属性
| 名称 | 湖南省邵阳市邵阳县黄亭市镇中学2016-2017学年八年级数学(下)第三次月考试卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 29.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-28 00:00:00 | ||
图片预览

文档简介
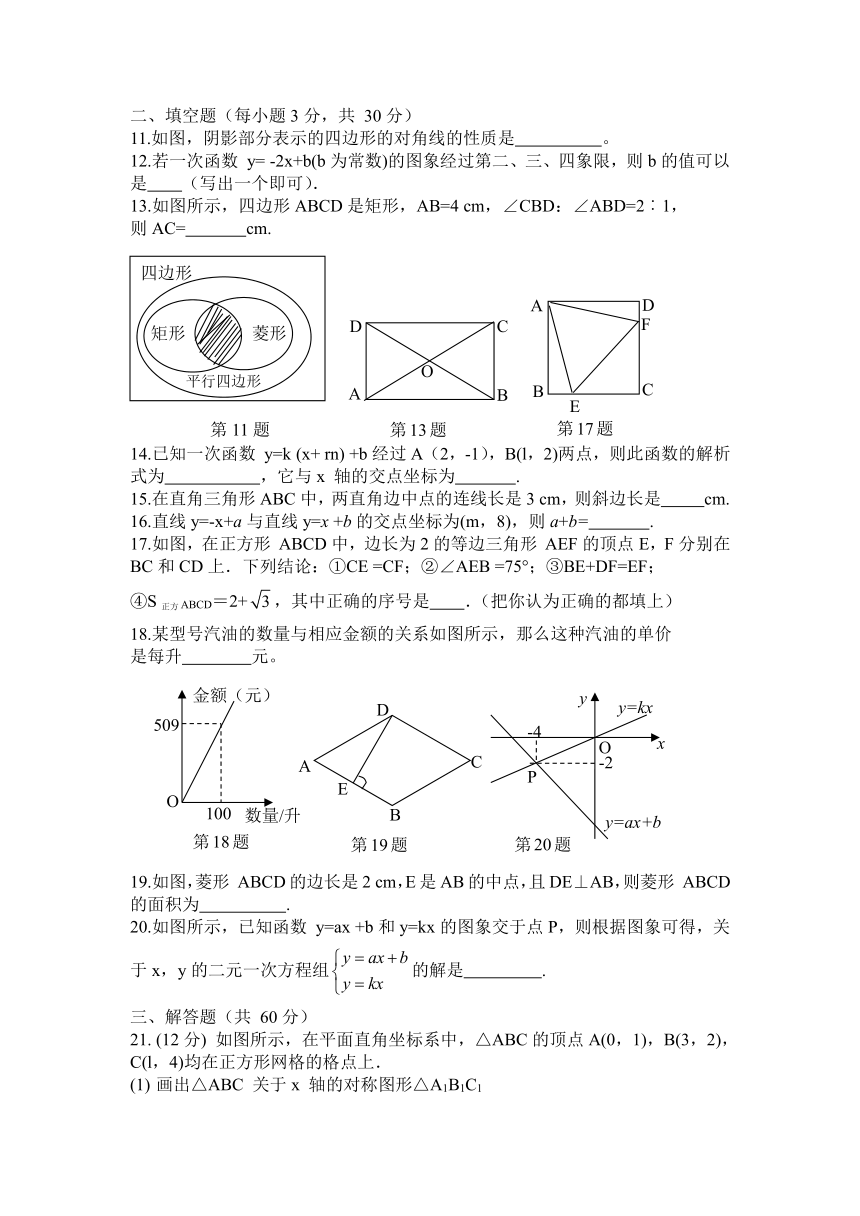
2016--2017学年八年级数学(下)第三次月考试卷
一、选择题(每小题3分,共
30分)
1.已知点P(0,m)在y
轴的负半轴上,则点M(-m,-m+1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在直角坐标系中,点M,N在同一个正比例函数图象上的是(
)
M(2,-3),N(-4,6)
B.M(-2,3),N(4,6)
C.M(-2,-3),N(4,-6)
D.M(2,3),N(-4,6)
3.如图,已知正方形ABCD的两条对角线相交于点O,
那么此图中等腰直角三角形有(
)
A.4个;
B.6个;
C.8个;
D.10个;
4.已知函数y=2x+b的图象过点(2,3),当
x=3时,
y的值是(
)
A.4;
B.5;
C.8;
D.7
;
5.如图,平行四边形ABCD中,AD=5,AB=3,
BE
平分∠ABC交AD边于点E,则线段AE、
ED的长度分别为(
)
A.2和3;B.3和2;C.4和1;D.1和4;
6.如图,一次函数y=mx+n与y=mnx(mn≠0)在同一平面直角坐标系
中的图象可能是(
)
A.(1)和(3);
B.(2)和(3);
C.(1)和(4);
D.(3)和(4);
7.小明的父亲饭后散步,从家中走走20
min到一个离家家900
m的报亭看10
min的报纸后,用15
min返回家中,下列图形中表示小明父亲离家的距y与时间x
之间的关系的是(
)
8.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是(
)
A.(3,-3);B.(-3,3);
C.(3,3)或(-3,-3);D.(3,-3)或(-3,3);
9.如图所示,矩形ABCD的对角线AC,BD相交于点O,
CE∥BD,DE∥AC,若AC=4,则四边形
OCED的周长为(
)
A.4;
B.8;
C.10;
D.l2;
10、已知点(-2,y1),(2,y2)在直线y=2x+3上,则y1,y2
的大小关系是(
)
A.y1B.y1=y2;
C.y1>y2;
D.不能比较;
二、填空题(每小题3分,共
30分)
11.如图,阴影部分表示的四边形的对角线的性质是
。
12.若一次函数
y=
-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以
是
(写出一个即可).
13.如图所示,四边形ABCD是矩形,AB=4
cm,∠CBD:∠ABD=2︰1,
则AC=
cm.
14.已知一次函数
y=k
(x+
rn)
+b经过A(2,-1),B(l,2)两点,则此函数的解析式为
,它与x
轴的交点坐标为
.
15.在直角三角形ABC中,两直角边中点的连线长是3
cm,则斜边长是
cm.
16.直线y=-x+a与直线y=x
+b的交点坐标为(m,8),则a+b=
.
17.如图,在正方形
ABCD中,边长为2的等边三角形
AEF的顶点E,F分别在BC和CD上.下列结论:①CE
=CF;②∠AEB
=75°;③BE+DF=EF;
④S正方ABCD=2+,其中正确的序号是
.(把你认为正确的都填上)
18.某型号汽油的数量与相应金额的关系如图所示,那么这种汽油的单价
是每升
元。
19.如图,菱形
ABCD的边长是2
cm,E是AB的中点,且DE⊥AB,则菱形
ABCD的面积为
.
20.如图所示,已知函数
y=ax
+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组的解是
.
三、解答题(共
60分)
21.
(12分)
如图所示,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),
C(l,4)均在正方形网格的格点上.
画出△ABC
关于x
轴的对称图形△A1B1C1
将△A1B1C1沿x
轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标;
22.(12分)已知一次函数的图
象经过点A(-3,4),,B(
-l,-
2).
(1)求出这个一次函数的解析式;
(2)求△AOB的面积,
23,(12分)如图所示,在正方形ABCD中,E是对角线AC上的一点,EF⊥CD于点F,EG⊥AD于点G.求证:BE
=GF
24.(9分)已知yl=2x+l,y2=x-3,求当
x取何值时,
(1)
yl=y2;(2)
yl>y2;;(3)
yl25.(15分)某乡
A、B两村盛产柑橘,A
村有柑橘
200吨,B
村有柑橘
300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存
240吨,D仓库可储存
260吨;从A
村运往C、D两处的费用分别为每吨20
元和25
元,从B
村运往C、D两处的费用分别为每吨15
元和18元,设从A
村运往C仓库的柑橘质量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元,
(1)请填写下表,并求出yA、yB元与x之间的函数解析式;
(2)讨论A、B两村中,哪个村的运费较少;
(3)考虑到
B
村的经济承受能力,B
村的柑橘运费不得超过4
830
元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值
运地/收地
C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
参考答案
一、1.A
2.A
3.C
4.B
5.B
6.D
7.D
8.D9.B
10.A
二、11.相等且互相垂直平分;
12,-1(答案不唯一);
13、;14、y=-3x+5,(,0);15、6;16、16;17、①②④;18、5.09;
19、;20、;
三、21、图略,A2(-3,-1),B2
(0,-2),C2
(-2,-
4);
22.(1)y=-3x
-5;
(2)在y=-3x
-5中令y=0,解得,即:直线AB与x轴交于点C(,0).
∴S△AOB=
S△AOB+
S△AOB=
23.证明:连接DE,∵四边形ABCD是正方形,∴∠ADC=
90°,
又∴GE⊥AD,EF⊥CD,∴四边形GEFD是矩形,∴GF
=ED.
∵四边形ABCD是正方形,∴BC=CD,∠BCE=∠DCE=45°.
∴△BEC:≌△DEC,∴BE=
ED,∴BE=
GF.
24.(1)∵y1=
2x
+1,y2=x-3,y1=
y2,∴2x
+1=
x-3,∴x=-4,
即当
x=-4时,y1=
y2,
(2)当
x>-4时,y1>y2,
(3)当
x<-4时,y1<
y2,
运地/收地
C
D
总计
A
x吨
(200-x)
200吨
B
(240-x)
(60+x)
300吨
总计
240吨
260吨
500吨
25.
(1)填空:
yA=
-
5x+5
000(0≤x≤200);yB
=3x+4
680(0≤x≤200).
(2)分三种情况:若yA>
yB,即:x<40;若yA=
yB
即:x=40;
若yA<
yB即:x>40;
∴当x<40时,B
村运费较少;当
x=
40时,两村运费相等;
当x>40时,A
村运费较少;
(3)由yB≤4
830得3x+4
680≤4
830,
∴x≤50.
设两村运费之和为y,∴
y=yA+yB=-5x+5
000+3x+4
680=-2x+9680(0≤x≤50).
由
y随x增大而减小,得当x=50时,y有最小值为y
=-2×50十9
680=9
580(元).
这时240-x
=190,60+x
=110,200-x=150.
答:当
A
村往C、D仓库分别运50吨与150吨,B
村往C、D仓库分别运190吨与110吨时运费之和最小,最小费用为9
580
元.
A
B
C
D
O
第3题
A
B
C
D
E
第5题
O
x
y
(1)
O
x
y
(2)
O
x
y
(3)
O
x
y
(4)
O
x
y
A
900
20
45
O
x
y
B
900
20
45
O
x
y
C
900
20
45
x
O
y
D
900
20
45
A
B
C
D
O
E
第9题
四边形
平行四边形
矩形
菱形
第11题
A
B
C
D
E
第17题
F
A
B
C
D
O
第13题
P
O
x
y
y=kx
-4
-2
y=ax+b
第20题
数量/升
金额(元)
O
100
509
第18题
A
B
C
D
E
第19题
x
y
A
B
C
O
A
B
C
D
E
F
G
一、选择题(每小题3分,共
30分)
1.已知点P(0,m)在y
轴的负半轴上,则点M(-m,-m+1)在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在直角坐标系中,点M,N在同一个正比例函数图象上的是(
)
M(2,-3),N(-4,6)
B.M(-2,3),N(4,6)
C.M(-2,-3),N(4,-6)
D.M(2,3),N(-4,6)
3.如图,已知正方形ABCD的两条对角线相交于点O,
那么此图中等腰直角三角形有(
)
A.4个;
B.6个;
C.8个;
D.10个;
4.已知函数y=2x+b的图象过点(2,3),当
x=3时,
y的值是(
)
A.4;
B.5;
C.8;
D.7
;
5.如图,平行四边形ABCD中,AD=5,AB=3,
BE
平分∠ABC交AD边于点E,则线段AE、
ED的长度分别为(
)
A.2和3;B.3和2;C.4和1;D.1和4;
6.如图,一次函数y=mx+n与y=mnx(mn≠0)在同一平面直角坐标系
中的图象可能是(
)
A.(1)和(3);
B.(2)和(3);
C.(1)和(4);
D.(3)和(4);
7.小明的父亲饭后散步,从家中走走20
min到一个离家家900
m的报亭看10
min的报纸后,用15
min返回家中,下列图形中表示小明父亲离家的距y与时间x
之间的关系的是(
)
8.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是(
)
A.(3,-3);B.(-3,3);
C.(3,3)或(-3,-3);D.(3,-3)或(-3,3);
9.如图所示,矩形ABCD的对角线AC,BD相交于点O,
CE∥BD,DE∥AC,若AC=4,则四边形
OCED的周长为(
)
A.4;
B.8;
C.10;
D.l2;
10、已知点(-2,y1),(2,y2)在直线y=2x+3上,则y1,y2
的大小关系是(
)
A.y1
C.y1>y2;
D.不能比较;
二、填空题(每小题3分,共
30分)
11.如图,阴影部分表示的四边形的对角线的性质是
。
12.若一次函数
y=
-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以
是
(写出一个即可).
13.如图所示,四边形ABCD是矩形,AB=4
cm,∠CBD:∠ABD=2︰1,
则AC=
cm.
14.已知一次函数
y=k
(x+
rn)
+b经过A(2,-1),B(l,2)两点,则此函数的解析式为
,它与x
轴的交点坐标为
.
15.在直角三角形ABC中,两直角边中点的连线长是3
cm,则斜边长是
cm.
16.直线y=-x+a与直线y=x
+b的交点坐标为(m,8),则a+b=
.
17.如图,在正方形
ABCD中,边长为2的等边三角形
AEF的顶点E,F分别在BC和CD上.下列结论:①CE
=CF;②∠AEB
=75°;③BE+DF=EF;
④S正方ABCD=2+,其中正确的序号是
.(把你认为正确的都填上)
18.某型号汽油的数量与相应金额的关系如图所示,那么这种汽油的单价
是每升
元。
19.如图,菱形
ABCD的边长是2
cm,E是AB的中点,且DE⊥AB,则菱形
ABCD的面积为
.
20.如图所示,已知函数
y=ax
+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组的解是
.
三、解答题(共
60分)
21.
(12分)
如图所示,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),
C(l,4)均在正方形网格的格点上.
画出△ABC
关于x
轴的对称图形△A1B1C1
将△A1B1C1沿x
轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标;
22.(12分)已知一次函数的图
象经过点A(-3,4),,B(
-l,-
2).
(1)求出这个一次函数的解析式;
(2)求△AOB的面积,
23,(12分)如图所示,在正方形ABCD中,E是对角线AC上的一点,EF⊥CD于点F,EG⊥AD于点G.求证:BE
=GF
24.(9分)已知yl=2x+l,y2=x-3,求当
x取何值时,
(1)
yl=y2;(2)
yl>y2;;(3)
yl
A、B两村盛产柑橘,A
村有柑橘
200吨,B
村有柑橘
300吨,现将这些柑橘运到C、D两个冷藏仓库,已知C仓库可储存
240吨,D仓库可储存
260吨;从A
村运往C、D两处的费用分别为每吨20
元和25
元,从B
村运往C、D两处的费用分别为每吨15
元和18元,设从A
村运往C仓库的柑橘质量为x吨,A、B两村运往两仓库的柑橘运输费用分别为yA元和yB元,
(1)请填写下表,并求出yA、yB元与x之间的函数解析式;
(2)讨论A、B两村中,哪个村的运费较少;
(3)考虑到
B
村的经济承受能力,B
村的柑橘运费不得超过4
830
元.在这种情况下,请问怎样调运,才能使两村运费之和最小?求出这个最小值
运地/收地
C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
参考答案
一、1.A
2.A
3.C
4.B
5.B
6.D
7.D
8.D9.B
10.A
二、11.相等且互相垂直平分;
12,-1(答案不唯一);
13、;14、y=-3x+5,(,0);15、6;16、16;17、①②④;18、5.09;
19、;20、;
三、21、图略,A2(-3,-1),B2
(0,-2),C2
(-2,-
4);
22.(1)y=-3x
-5;
(2)在y=-3x
-5中令y=0,解得,即:直线AB与x轴交于点C(,0).
∴S△AOB=
S△AOB+
S△AOB=
23.证明:连接DE,∵四边形ABCD是正方形,∴∠ADC=
90°,
又∴GE⊥AD,EF⊥CD,∴四边形GEFD是矩形,∴GF
=ED.
∵四边形ABCD是正方形,∴BC=CD,∠BCE=∠DCE=45°.
∴△BEC:≌△DEC,∴BE=
ED,∴BE=
GF.
24.(1)∵y1=
2x
+1,y2=x-3,y1=
y2,∴2x
+1=
x-3,∴x=-4,
即当
x=-4时,y1=
y2,
(2)当
x>-4时,y1>y2,
(3)当
x<-4时,y1<
y2,
运地/收地
C
D
总计
A
x吨
(200-x)
200吨
B
(240-x)
(60+x)
300吨
总计
240吨
260吨
500吨
25.
(1)填空:
yA=
-
5x+5
000(0≤x≤200);yB
=3x+4
680(0≤x≤200).
(2)分三种情况:若yA>
yB,即:x<40;若yA=
yB
即:x=40;
若yA<
yB即:x>40;
∴当x<40时,B
村运费较少;当
x=
40时,两村运费相等;
当x>40时,A
村运费较少;
(3)由yB≤4
830得3x+4
680≤4
830,
∴x≤50.
设两村运费之和为y,∴
y=yA+yB=-5x+5
000+3x+4
680=-2x+9680(0≤x≤50).
由
y随x增大而减小,得当x=50时,y有最小值为y
=-2×50十9
680=9
580(元).
这时240-x
=190,60+x
=110,200-x=150.
答:当
A
村往C、D仓库分别运50吨与150吨,B
村往C、D仓库分别运190吨与110吨时运费之和最小,最小费用为9
580
元.
A
B
C
D
O
第3题
A
B
C
D
E
第5题
O
x
y
(1)
O
x
y
(2)
O
x
y
(3)
O
x
y
(4)
O
x
y
A
900
20
45
O
x
y
B
900
20
45
O
x
y
C
900
20
45
x
O
y
D
900
20
45
A
B
C
D
O
E
第9题
四边形
平行四边形
矩形
菱形
第11题
A
B
C
D
E
第17题
F
A
B
C
D
O
第13题
P
O
x
y
y=kx
-4
-2
y=ax+b
第20题
数量/升
金额(元)
O
100
509
第18题
A
B
C
D
E
第19题
x
y
A
B
C
O
A
B
C
D
E
F
G
同课章节目录
