江苏省镇江市八年级数学下册9.5三角形的中位线教案(新版)苏科版
文档属性
| 名称 | 江苏省镇江市八年级数学下册9.5三角形的中位线教案(新版)苏科版 |

|
|
| 格式 | zip | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-29 00:00:00 | ||
图片预览

文档简介
三角形的中位线
学习目标:
1.探索并掌握三角形中位线的概念、性质;
2.会利用三角形的中位线的性质解决有关问题;
3.经历探索三角形中位线性质的过程,体会转化的思想方法.
学习重点:会利用三角形的中位线的性质解决有关问题.
学习难点:经历探索三角形中位线性质的过程,体会转化的思想方法.
学习过程:
课前准备
1、连接三角形两边
的线段叫做三角形的
2、三角形的中位线
,并且等于
3、如果一个三角形的面积为8cm2,那么它有
条中位线,这些中位线所围成的三角形的面积为_______cm2.
4、如果四边形ABCD的四边中点依次是E、F、G、H,那么四边形EFGH是
____形.如果AC=24cm,BD=32cm,那么四边形EFGH的周长等于______cm;
探索新知
1、情境创设:
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼与一个平行四边形
2、动手操作
(1)、剪一个三角形记为△ABC;
(2)、分别取AB、AC的中点D、E,连接DE;
(3)、沿DE将△ABC剪成两部分,将△ADE绕点E旋转180°,得四边形BCFD,如图Ⅰ
观察:四边形BCFD是平行四边形吗?
3、新知归纳
概念:三角形中位线:
性质:三角形中位线性质:
AD=DB、AE=EC,DE∥BC且DE
=
BC
从今天开始我们就一起研究这样一条特殊的线段-----三角形的中位线
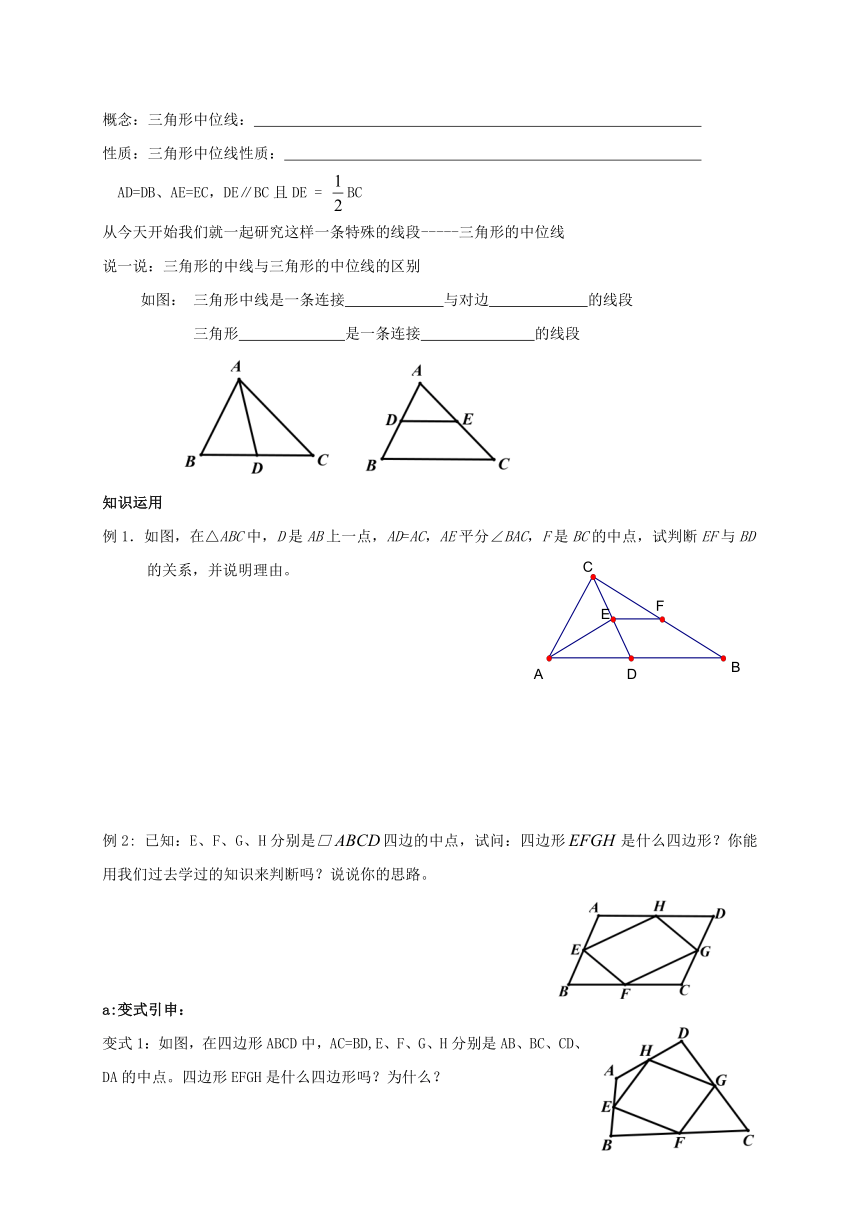
说一说:三角形的中线与三角形的中位线的区别
如图:
三角形中线是一条连接
与对边
的线段
三角形
是一条连接
的线段
知识运用
例1.如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠BAC,F是BC的中点,试判断EF与BD的关系,并说明理由。
例2:
已知:E、F、G、H分别是□四边的中点,试问:四边形是什么四边形?你能用我们过去学过的知识来判断吗?说说你的思路。
a:变式引申:
变式1:如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
变式2:如图,在四边形ABCD中,AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
变式3:如图,在四边形ABCD中,AC=BD且AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
b:总结归纳:
(1)当例2中四边形ABCD
的对角线AC与BD满足
条件时,四边形EFGH菱形。
(2)当例2中四边形ABCD
的对角线AC与BD满足
条件时,四边形EFGH矩形。
(3)当例2中四边形ABCD的对角线AC与BD满足
条件时,四边形EFGH正方形
类比:
(1)
若将例2中“四边形ABCD”改为“平行四边形ABCD”,那么四边形EFGH是
形。
(2)
若将例2中“四边形ABCD”改为“矩形ABCD”,那么四边形EFGH是
形。
(3)若将例2中“四边形ABCD”改为“菱形ABCD”,那么四边形EFGH是
形。
(4)若将例2中“四边形ABCD”改为“正方形ABCD”,那么四边形EFGH是
形。
当堂反馈
1、若三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm。.
2、已知D、E、F是⊿ABC三边的中点。
(1)、若⊿DEF的周长是20㎝,则⊿ABC的周长为__________㎝;
(2)、图中四个小三角形有何关系:_____________;;
3、一个三角形的周长是12cm,面积是8cm2,则这个三角形各边中点
围成的三角形的周长是
cm,面积为_______cm2。.
4、如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E。
(1)、若DE的长为36m,求A、B两地间的距离;
(2)、如果D、E两点间还有阻隔,你有什么解决办法?
5、如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,那么△EFG是什么三角形?请说明理由.
6、如图,在△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,
试判断四边形EFGD的形状,并说明理由.
课后作业
1、例1中①若四边形ABCD是矩形,则四边形EFGH是
形。②若四边形ABCD是菱形,则四边形EFGH是
形。
2、如图,已知菱形ABCD的对角线相交于点O,E、F分别是AB、AD的中点,试问线段OE与OF有什么关系,并说明理由。
3、已知三角形3条中位线的比为3:5:6,三角形的周长是112cm,求三条中位线长。
4、如图,在四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD,分别交于点E、F,试说明:∠BEN=∠NFC(提示:连接BD并取中点O,再连接MO、NO).
5、已知:的周长为,面积为,连接各边中点得,再连接各边中点得
……,则第1次连接所得的周长=
,面积=
;第2次连接所得的周长=
,面积=
;第3次连接所得的周长=
,面积=
,┉┉第次连接所得的周长=
,面积=
学习目标:
1.探索并掌握三角形中位线的概念、性质;
2.会利用三角形的中位线的性质解决有关问题;
3.经历探索三角形中位线性质的过程,体会转化的思想方法.
学习重点:会利用三角形的中位线的性质解决有关问题.
学习难点:经历探索三角形中位线性质的过程,体会转化的思想方法.
学习过程:
课前准备
1、连接三角形两边
的线段叫做三角形的
2、三角形的中位线
,并且等于
3、如果一个三角形的面积为8cm2,那么它有
条中位线,这些中位线所围成的三角形的面积为_______cm2.
4、如果四边形ABCD的四边中点依次是E、F、G、H,那么四边形EFGH是
____形.如果AC=24cm,BD=32cm,那么四边形EFGH的周长等于______cm;
探索新知
1、情境创设:
怎样将一张三角形纸片剪成两部分,使分成的两部分能拼与一个平行四边形
2、动手操作
(1)、剪一个三角形记为△ABC;
(2)、分别取AB、AC的中点D、E,连接DE;
(3)、沿DE将△ABC剪成两部分,将△ADE绕点E旋转180°,得四边形BCFD,如图Ⅰ
观察:四边形BCFD是平行四边形吗?
3、新知归纳
概念:三角形中位线:
性质:三角形中位线性质:
AD=DB、AE=EC,DE∥BC且DE
=
BC
从今天开始我们就一起研究这样一条特殊的线段-----三角形的中位线
说一说:三角形的中线与三角形的中位线的区别
如图:
三角形中线是一条连接
与对边
的线段
三角形
是一条连接
的线段
知识运用
例1.如图,在△ABC中,D是AB上一点,AD=AC,AE平分∠BAC,F是BC的中点,试判断EF与BD的关系,并说明理由。
例2:
已知:E、F、G、H分别是□四边的中点,试问:四边形是什么四边形?你能用我们过去学过的知识来判断吗?说说你的思路。
a:变式引申:
变式1:如图,在四边形ABCD中,AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
变式2:如图,在四边形ABCD中,AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
变式3:如图,在四边形ABCD中,AC=BD且AC垂直BD,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是什么四边形吗?为什么?
b:总结归纳:
(1)当例2中四边形ABCD
的对角线AC与BD满足
条件时,四边形EFGH菱形。
(2)当例2中四边形ABCD
的对角线AC与BD满足
条件时,四边形EFGH矩形。
(3)当例2中四边形ABCD的对角线AC与BD满足
条件时,四边形EFGH正方形
类比:
(1)
若将例2中“四边形ABCD”改为“平行四边形ABCD”,那么四边形EFGH是
形。
(2)
若将例2中“四边形ABCD”改为“矩形ABCD”,那么四边形EFGH是
形。
(3)若将例2中“四边形ABCD”改为“菱形ABCD”,那么四边形EFGH是
形。
(4)若将例2中“四边形ABCD”改为“正方形ABCD”,那么四边形EFGH是
形。
当堂反馈
1、若三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是
cm。.
2、已知D、E、F是⊿ABC三边的中点。
(1)、若⊿DEF的周长是20㎝,则⊿ABC的周长为__________㎝;
(2)、图中四个小三角形有何关系:_____________;;
3、一个三角形的周长是12cm,面积是8cm2,则这个三角形各边中点
围成的三角形的周长是
cm,面积为_______cm2。.
4、如图,A、B两地被建筑物阻隔,为测量A、B两地间的距离,在地面上选一点C,连接CA、CB,分别取CA、CB的中点D、E。
(1)、若DE的长为36m,求A、B两地间的距离;
(2)、如果D、E两点间还有阻隔,你有什么解决办法?
5、如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,连接EF、EG、FG,那么△EFG是什么三角形?请说明理由.
6、如图,在△ABC中,中线BD、CE相交于点O,F、G分别是OB、OC的中点,
试判断四边形EFGD的形状,并说明理由.
课后作业
1、例1中①若四边形ABCD是矩形,则四边形EFGH是
形。②若四边形ABCD是菱形,则四边形EFGH是
形。
2、如图,已知菱形ABCD的对角线相交于点O,E、F分别是AB、AD的中点,试问线段OE与OF有什么关系,并说明理由。
3、已知三角形3条中位线的比为3:5:6,三角形的周长是112cm,求三条中位线长。
4、如图,在四边形ABCD中,AB=CD,M、N分别是AD、BC的中点,延长BA、NM、CD,分别交于点E、F,试说明:∠BEN=∠NFC(提示:连接BD并取中点O,再连接MO、NO).
5、已知:的周长为,面积为,连接各边中点得,再连接各边中点得
……,则第1次连接所得的周长=
,面积=
;第2次连接所得的周长=
,面积=
;第3次连接所得的周长=
,面积=
,┉┉第次连接所得的周长=
,面积=
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
