山东省聊城市临清市2016-2017学年八年级(下)期中数学试卷(解析版)
文档属性
| 名称 | 山东省聊城市临清市2016-2017学年八年级(下)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 247.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-29 08:57:46 | ||
图片预览


文档简介
2016-2017学年山东省聊城市临清市八年级(下)期中数学试卷
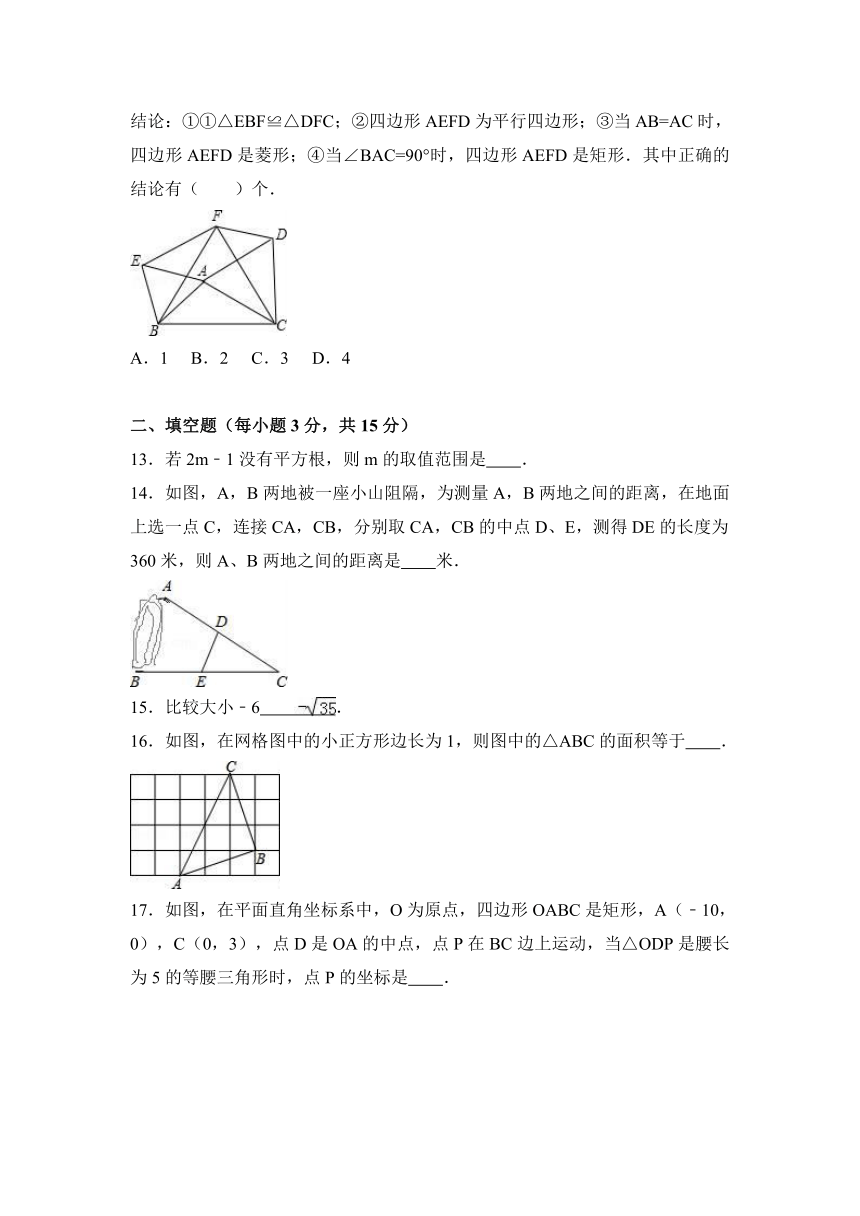
一、选择题(每小题3分,共12小题)
1.9的算术平方根是( )
A.﹣3
B.3
C.
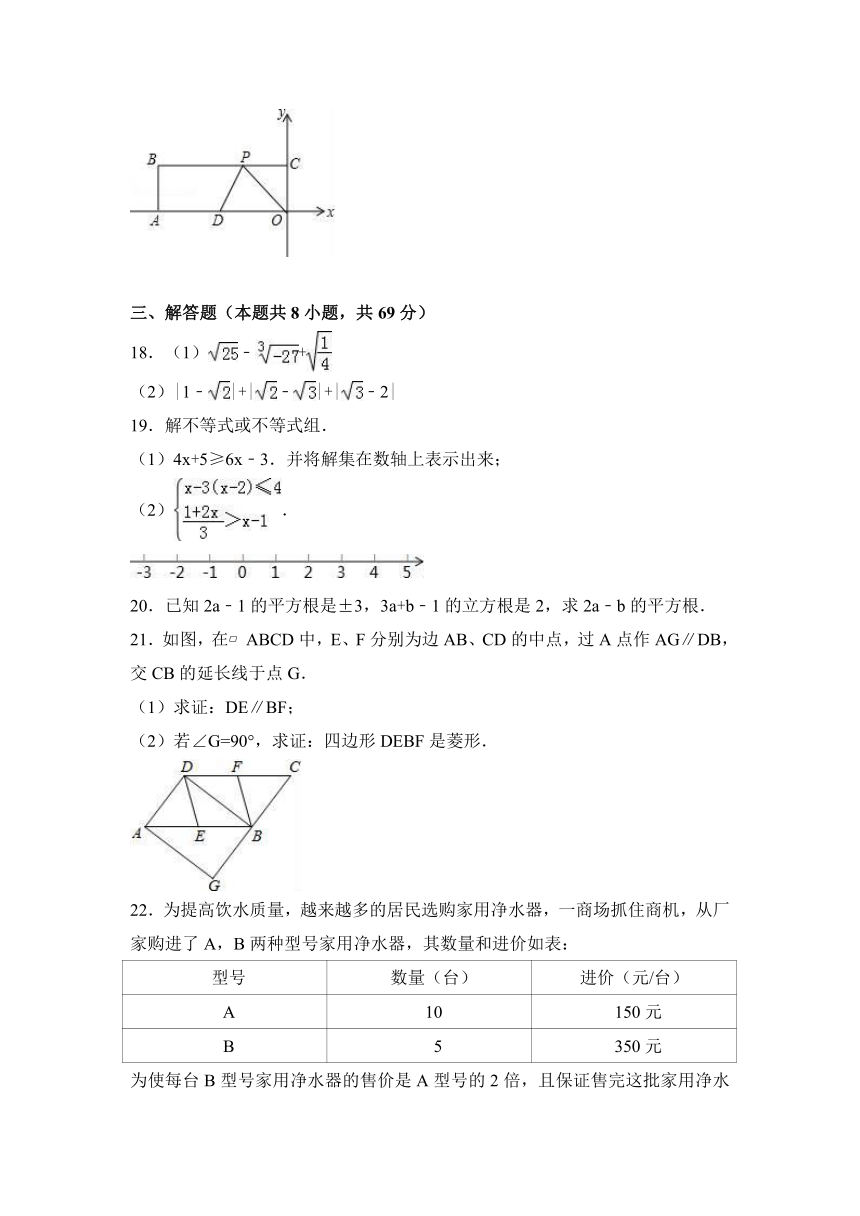
D.±3
2.在 ABCD中,若∠A+∠C=200°,则∠B的大小为( )
A.160°
B.100°
C.80°
D.60°
3.,38,0,π,,,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
A.1
B.2
C.3
D.4
4.在 ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )
A.11
B.12
C.13
D.14
5.若m>n,下列不等式不一定成立的是( )
A.m﹣2>n﹣2
B.>
C.m2>n2
D.2m+1>2n+1
6.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为( )
A.962
B.48cm2
C.24cm2
D.12cm2
7.x的2倍减去7的差不大于﹣1,可列关系式为( )
A.2x﹣7≤﹣1
B.2x﹣7<﹣1
C.2x﹣7=﹣1
D.2x﹣7≥﹣1
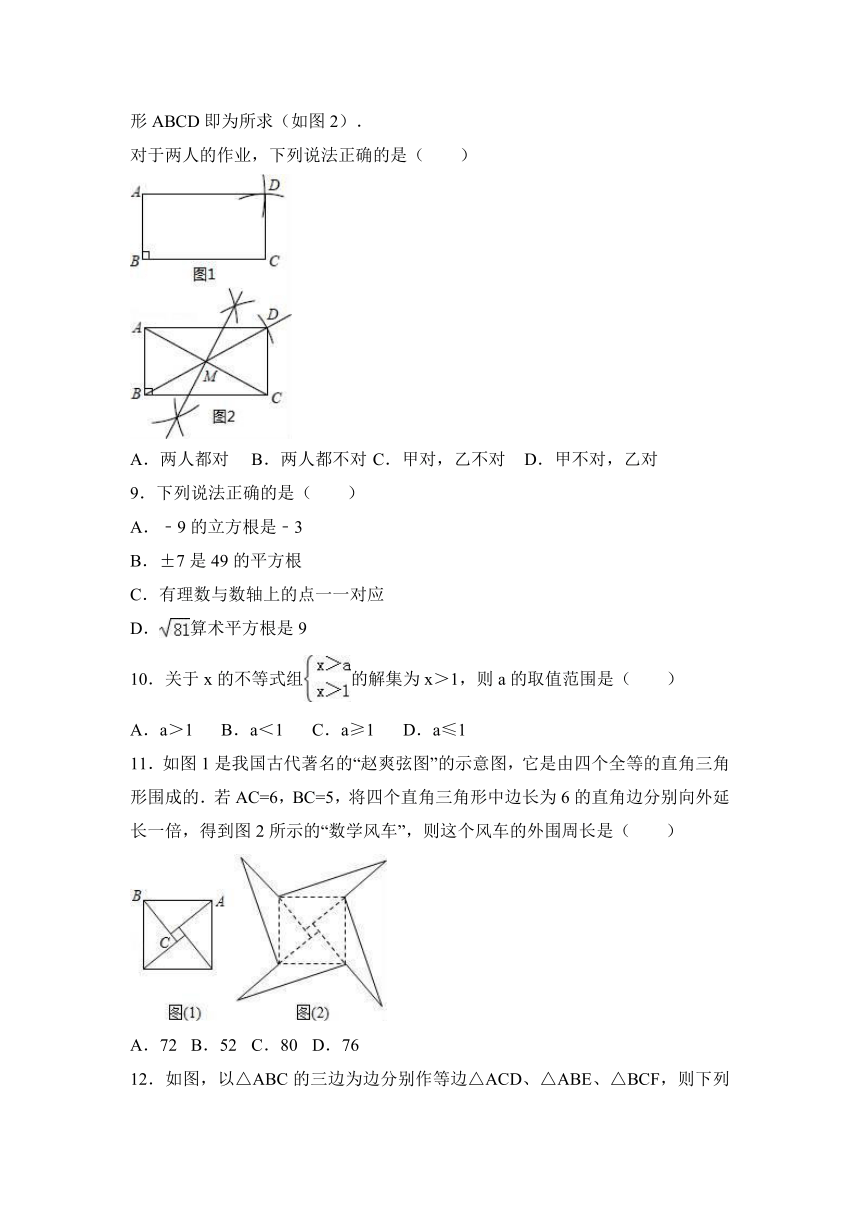
8.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.
以下是甲、乙两同学的作业:
甲:
1.以点C为圆心,AB长为半径画弧;
2.以点A为圆心,BC长为半径画弧;
3.两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1).
乙:
1.连接AC,作线段AC的垂直平分线,交AC于点M;
2.连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
9.下列说法正确的是( )
A.﹣9的立方根是﹣3
B.±7是49的平方根
C.有理数与数轴上的点一一对应
D.算术平方根是9
10.关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
11.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72
B.52
C.80
D.76
12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC时,四边形AEFD是菱形;④当∠BAC=90°时,四边形AEFD是矩形.其中正确的结论有( )个.
A.1
B.2
C.3
D.4
二、填空题(每小题3分,共15分)
13.若2m﹣1没有平方根,则m的取值范围是 .
14.如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是 米.
15.比较大小﹣6 .
16.如图,在网格图中的小正方形边长为1,则图中的△ABC的面积等于 .
17.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 .
三、解答题(本题共8小题,共69分)
18.(1)﹣+
(2)|1﹣|+|﹣|+|﹣2|
19.解不等式或不等式组.
(1)4x+5≥6x﹣3.并将解集在数轴上表示出来;
(2).
20.已知2a﹣1的平方根是±3,3a+b﹣1的立方根是2,求2a﹣b的平方根.
21.如图,在 ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
22.为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:
型号
数量(台)
进价(元/台)
A
10
150元
B
5
350元
为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价﹣进价)
23.甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
24.对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[﹣7.5]=﹣8.
(1)若[a]=﹣3,那么a的取值范围是 ;
(2)若[]=2,求满足条件的所有正整数a.
25.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
2016-2017学年山东省聊城市临清市八年级(下)期中数学试卷
参考答案与试题解析
一、选择题(每小题3分,共12小题)
1.9的算术平方根是( )
A.﹣3
B.3
C.
D.±3
【考点】22:算术平方根.
【分析】根据算术平方根的定义解答.
【解答】解:∵32=9,
∴9的算术平方根是3.
故选B.
2.在 ABCD中,若∠A+∠C=200°,则∠B的大小为( )
A.160°
B.100°
C.80°
D.60°
【考点】L5:平行四边形的性质.
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=200°,
∴∠A=100°,
∴∠B=180°﹣∠A=80°.
故选C.
3.,38,0,π,,,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
A.1
B.2
C.3
D.4
【考点】26:无理数.
【分析】根据无理数的定义求解即可.
【解答】解:,π,0.1010010001…(相连两个1之间依次多一个0)是无理数,
故选:C.
4.在 ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )
A.11
B.12
C.13
D.14
【考点】L5:平行四边形的性质.
【分析】根据平行四边形对角线互相平分,求出OA、OB即可解决问题.
【解答】解:如图,∵四边形ABCD是平行四边形,
∴AO=OC=AC=4,BO=OD=BD=3,
∵AB=5,
∴△AOB的周长为OA+OB+AB=4+3+5=12.
故选B.
5.若m>n,下列不等式不一定成立的是( )
A.m﹣2>n﹣2
B.>
C.m2>n2
D.2m+1>2n+1
【考点】C2:不等式的性质.
【分析】根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变,可得答案.
【解答】解:A、不等式的两边都减2,不等号的方向不变,故A错误;
B、不等式的两边都除以2,不等号的方向不变,故B错误;
C、如m=2,n=3,m>n,m2>n2,故C正确;
D、不等式的两边都乘以2,不等号的方向不变;不等式的两边都加2,不等号的方向不变;故D错误;
故选:C.
6.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为( )
A.962
B.48cm2
C.24cm2
D.12cm2
【考点】L8:菱形的性质.
【分析】设菱形的对角线分别为3a,4a,列出方程求出a2,根据菱形的面积=×3a×4a=6a2即可解决问题.
【解答】解:设菱形的对角线分别为3a,4a,
∵菱形的周长为40,
∴菱形的边长为10,
∴()2+(2a)2=102,
∴a2=16,
∴菱形的面积=×3a×4a=6a2=96.
故选A.
7.x的2倍减去7的差不大于﹣1,可列关系式为( )
A.2x﹣7≤﹣1
B.2x﹣7<﹣1
C.2x﹣7=﹣1
D.2x﹣7≥﹣1
【考点】C8:由实际问题抽象出一元一次不等式.
【分析】理解:不大于﹣1,即是小于或等于﹣1.
【解答】解:根据题意,得
2x﹣7≤﹣1.
故选:A.
8.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.
以下是甲、乙两同学的作业:
甲:
1.以点C为圆心,AB长为半径画弧;
2.以点A为圆心,BC长为半径画弧;
3.两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1).
乙:
1.连接AC,作线段AC的垂直平分线,交AC于点M;
2.连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
【考点】N3:作图—复杂作图;LC:矩形的判定.
【分析】先由两组对边分别相等的四边形是平行四边形得出四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形判断甲的作业正确;
先由对角线互相平分的四边形是平行四边形得出四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形判断乙的作业也正确.
【解答】解:由甲同学的作业可知,CD=AB,AD=BC,
∴四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴ ABCD是矩形.
所以甲的作业正确;
由乙同学的作业可知,CM=AM,MD=MB,
∴四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴ ABCD是矩形.
所以乙的作业正确;
故选:A.
9.下列说法正确的是( )
A.﹣9的立方根是﹣3
B.±7是49的平方根
C.有理数与数轴上的点一一对应
D.算术平方根是9
【考点】29:实数与数轴;22:算术平方根;24:立方根.
【分析】根据开方运算,可得答案.
【解答】解:﹣9的立方根是,故A不符合题意;
B、±7是49的平方根,故B符合题意;
C、实数与数轴上的点一一对应,故C不符合题意;
D、算术平方根是3,故D不符合题意;
故选:B.
10.关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
【考点】C3:不等式的解集.
【分析】解两个不等式后,根据其解集得出关于a的不等式,解答即可.
【解答】解:因为不等式组的解集为x>1,
所以可得a≤1,
故选D
11.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72
B.52
C.80
D.76
【考点】KR:勾股定理的证明.
【分析】由题意∠ACB为直角,利用勾股定理求得外围中一条边,又由AC延伸一倍,从而求得风车的一个轮子,进一步求得四个.
【解答】解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,则
x2=122+52=169
所以x=13
所以“数学风车”的周长是:(13+6)×4=76.
故选:D.
12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC时,四边形AEFD是菱形;④当∠BAC=90°时,四边形AEFD是矩形.其中正确的结论有( )个.
A.1
B.2
C.3
D.4
【考点】LC:矩形的判定;KD:全等三角形的判定与性质;KK:等边三角形的性质;L7:平行四边形的判定与性质;LA:菱形的判定与性质.
【分析】①由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;
②利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;
③当AE=AD时,ADFE是菱形,可以用邻边相等的平行四边形是菱形判断即可;
④当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形,由此即可判断;
【解答】解:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
.
∴△EBF≌△DFC(SAS),故①正确,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形;故②正确,
若AB=AC,则AE=AD,四边形AEFD是菱形此,
故△ABC满足AB=AC时,四边形AEFD是菱形;故③正确
若∠BAC=150°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°﹣60°﹣60°﹣90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
∴∠BAC=120°,四边形AEFD不是矩形;故④错误,
故选C.
二、填空题(每小题3分,共15分)
13.若2m﹣1没有平方根,则m的取值范围是 m< .
【考点】21:平方根.
【分析】根据平方根的定义可知2m﹣1<0,解不等式即可.
【解答】解:∵负数没有平方根,
∴2m﹣1<0,
解得:m.
故答案为:m.
14.如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是 720 米.
【考点】KX:三角形中位线定理.
【分析】首先根据D、E分别是CA,CB的中点,可得DE是△ABC的中位线,然后根据三角形的中位线定理,可得DE∥AB,且DE=,再根据DE的长度为360米,求出A、B两地之间的距离是多少米即可.
【解答】解:∵D、E分别是CA,CB的中点,
∴DE是△ABC的中位线,
∴DE∥AB,且DE=,
∵DE=360(米),
∴AB=360×2=720(米).
即A、B两地之间的距离是720米.
故答案为:720.
15.比较大小﹣6 < .
【考点】2A:实数大小比较.
【分析】求出=6,根据实数的大小比较法则比较即可.
【解答】解:∵=6,
∴﹣6<﹣,
故答案为:<.
16.如图,在网格图中的小正方形边长为1,则图中的△ABC的面积等于 5 .
【考点】K3:三角形的面积.
【分析】利用△ABC所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解.
【解答】解:△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3
=12﹣4﹣1.5﹣1.5
=12﹣7
=5.
故答案为:5.
17.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 (﹣4,3),或(﹣1,3),或(﹣9,3) .
【考点】LB:矩形的性质;D5:坐标与图形性质;KI:等腰三角形的判定;KQ:勾股定理.
【分析】先由矩形的性质求出OD=5,分情况讨论:(1)当OP=OD=5时;根据勾股定理求出PC,即可得出结果;
(2)当PD=OD=5时;①作PE⊥OA于E,根据勾股定理求出DE,得出PC,即可得出结果;
②作PF⊥OA于F,根据勾股定理求出DF,得出PC,即可得出结果.
【解答】解:∵A(﹣10,0),C(0,3),
∴OA=10,OC=3,
∵四边形OABC是矩形,
∴BC=OA=10,AB=OC=3,
∵D是OA的中点,
∴AD=OD=5,
分情况讨论:
(1)当OP=OD=5时,根据勾股定理得:PC==4,
∴点P的坐标为:(﹣4,3);
(2)当PD=OD=5时,分两种情况讨论:
①如图1所示:作PE⊥OA于E,
则∠PED=90°,DE==4,
∴PC=OE=5﹣4=1,
∴点P的坐标为:(﹣1,3);
②如图2所示:作PF⊥OA于F,
则DF==4,
∴PC=OF=5+4=9,
∴点P的坐标为:(﹣9,3);
综上所述:点P的坐标为:(﹣4,3),或(﹣1,3),或(﹣9,3);
故答案为:(﹣4,3),或(﹣1,3),或(﹣9,3).
三、解答题(本题共8小题,共69分)
18.(1)﹣+
(2)|1﹣|+|﹣|+|﹣2|
【考点】2C:实数的运算.
【分析】(1)首先计算开方,然后从左向右依次计算,求出算式的值是多少即可.
(2)根据绝对值的含义和求法,求出算式的值是多少即可.
【解答】解:(1)﹣+
=5﹣(﹣3)+0.5
=8+0.5
=8.5
(2)|1﹣|+|﹣|+|﹣2|
=﹣1+﹣+2﹣
=1
19.解不等式或不等式组.
(1)4x+5≥6x﹣3.并将解集在数轴上表示出来;
(2).
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集;C6:解一元一次不等式.
【分析】(1)移项,合并同类项,最后把不等式的解集在数轴上表示出来即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
【解答】解:(1)4x﹣6x≥﹣3﹣5,
﹣2x≥﹣8,
x≤4;
将解集在数轴上表示出来为:
(2),
由不等式①得:x≥1,
由不等式②得:x<4.
故不等式组的解集为1≤x<4.
20.已知2a﹣1的平方根是±3,3a+b﹣1的立方根是2,求2a﹣b的平方根.
【考点】21:平方根;24:立方根.
【分析】根据平方根和立方根得出2a﹣1=9,3a+b﹣1=8,求出a、b的值即可.
【解答】解:∵2a﹣1的平方根是±3,
∴2a﹣1=9,
a=5,
∵3a+b﹣1的立方根是2,
∴3a+b﹣1=8,
∴b=﹣6,
∴2a﹣b=16,
∴2a﹣b的平方根是±4.
21.如图,在 ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
【考点】L9:菱形的判定;L5:平行四边形的性质.
【分析】(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=AB,DF=CD.
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
22.为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:
型号
数量(台)
进价(元/台)
A
10
150元
B
5
350元
为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价﹣进价)
【考点】C9:一元一次不等式的应用.
【分析】设每台A型号家用净水器的售价为x元,则每台B型号家用净水器的售价是2x元,根据售完这批家用净水器的利润不低于1650元,列出不等式解答即可.
【解答】解:设每台A型家用净水器售价为x元,根据题意可得:
10(x﹣150)+5(2x﹣350)≥1650,
解得:x≥245,
故x的最小值为245,
答:每台A型号家用净水器的售价至少245元.
23.甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
【考点】KU:勾股定理的应用;KS:勾股定理的逆定理.
【分析】根据题意得出AC,AB的长,再利用勾股定理的逆定理得出△BAC是直角三角形,进而得出答案.
【解答】解:由题意可得:
AC=15×4=60(海里),
AB=20×4=80(海里),
AC2+AB2=602+802=10000,
BC2=10000,
故AC2+AB2=BC2,
∴△BAC是直角三角形,
∴∠BAC=90°,
180°﹣40°﹣90°=50°,
∴乙船航行的方向是南偏东50°(或东偏南40°).
24.对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[﹣7.5]=﹣8.
(1)若[a]=﹣3,那么a的取值范围是 ﹣3≤a<﹣2 ;
(2)若[]=2,求满足条件的所有正整数a.
【考点】CE:一元一次不等式组的应用.
【分析】(1)根据[a]=﹣3,得出﹣3≤a<﹣2,求出a的取值范围即可;
(2)根据题意得出2≤<3,求出x的取值范围,从而得出满足条件的所有正整数的解.
【解答】解:(1)∵[a]=﹣3,
∴a的取值范围是﹣3≤a<﹣2;
故答案为:﹣3≤a<﹣2.
(2)根据题意得:
2≤<3,
解得:2≤x<5,
∵为正整数,
∴a=2,3,4.
则满足条件的所有正整数a为2,3,4.
25.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【考点】LE:正方形的性质;KD:全等三角形的判定与性质;L8:菱形的性质.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
2017年5月29日
一、选择题(每小题3分,共12小题)
1.9的算术平方根是( )
A.﹣3
B.3
C.
D.±3
2.在 ABCD中,若∠A+∠C=200°,则∠B的大小为( )
A.160°
B.100°
C.80°
D.60°
3.,38,0,π,,,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
A.1
B.2
C.3
D.4
4.在 ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )
A.11
B.12
C.13
D.14
5.若m>n,下列不等式不一定成立的是( )
A.m﹣2>n﹣2
B.>
C.m2>n2
D.2m+1>2n+1
6.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为( )
A.962
B.48cm2
C.24cm2
D.12cm2
7.x的2倍减去7的差不大于﹣1,可列关系式为( )
A.2x﹣7≤﹣1
B.2x﹣7<﹣1
C.2x﹣7=﹣1
D.2x﹣7≥﹣1
8.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.
以下是甲、乙两同学的作业:
甲:
1.以点C为圆心,AB长为半径画弧;
2.以点A为圆心,BC长为半径画弧;
3.两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1).
乙:
1.连接AC,作线段AC的垂直平分线,交AC于点M;
2.连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
9.下列说法正确的是( )
A.﹣9的立方根是﹣3
B.±7是49的平方根
C.有理数与数轴上的点一一对应
D.算术平方根是9
10.关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
11.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72
B.52
C.80
D.76
12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC时,四边形AEFD是菱形;④当∠BAC=90°时,四边形AEFD是矩形.其中正确的结论有( )个.
A.1
B.2
C.3
D.4
二、填空题(每小题3分,共15分)
13.若2m﹣1没有平方根,则m的取值范围是 .
14.如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是 米.
15.比较大小﹣6 .
16.如图,在网格图中的小正方形边长为1,则图中的△ABC的面积等于 .
17.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 .
三、解答题(本题共8小题,共69分)
18.(1)﹣+
(2)|1﹣|+|﹣|+|﹣2|
19.解不等式或不等式组.
(1)4x+5≥6x﹣3.并将解集在数轴上表示出来;
(2).
20.已知2a﹣1的平方根是±3,3a+b﹣1的立方根是2,求2a﹣b的平方根.
21.如图,在 ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
22.为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:
型号
数量(台)
进价(元/台)
A
10
150元
B
5
350元
为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价﹣进价)
23.甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
24.对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[﹣7.5]=﹣8.
(1)若[a]=﹣3,那么a的取值范围是 ;
(2)若[]=2,求满足条件的所有正整数a.
25.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
2016-2017学年山东省聊城市临清市八年级(下)期中数学试卷
参考答案与试题解析
一、选择题(每小题3分,共12小题)
1.9的算术平方根是( )
A.﹣3
B.3
C.
D.±3
【考点】22:算术平方根.
【分析】根据算术平方根的定义解答.
【解答】解:∵32=9,
∴9的算术平方根是3.
故选B.
2.在 ABCD中,若∠A+∠C=200°,则∠B的大小为( )
A.160°
B.100°
C.80°
D.60°
【考点】L5:平行四边形的性质.
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠C=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=200°,
∴∠A=100°,
∴∠B=180°﹣∠A=80°.
故选C.
3.,38,0,π,,,0.1010010001…(相连两个1之间依次多一个0),其中无理数有( )个.
A.1
B.2
C.3
D.4
【考点】26:无理数.
【分析】根据无理数的定义求解即可.
【解答】解:,π,0.1010010001…(相连两个1之间依次多一个0)是无理数,
故选:C.
4.在 ABCD中,对角线AC、BD相交于点O,若AC=8,BD=6,AB=5,则△AOB的周长为( )
A.11
B.12
C.13
D.14
【考点】L5:平行四边形的性质.
【分析】根据平行四边形对角线互相平分,求出OA、OB即可解决问题.
【解答】解:如图,∵四边形ABCD是平行四边形,
∴AO=OC=AC=4,BO=OD=BD=3,
∵AB=5,
∴△AOB的周长为OA+OB+AB=4+3+5=12.
故选B.
5.若m>n,下列不等式不一定成立的是( )
A.m﹣2>n﹣2
B.>
C.m2>n2
D.2m+1>2n+1
【考点】C2:不等式的性质.
【分析】根据不等式的性质:不等式两边加(或减)同一个数(或式子),不等号的方向不变;不等式两边乘(或除以)同一个正数,不等号的方向不变;不等式两边乘(或除以)同一个负数,不等号的方向改变,可得答案.
【解答】解:A、不等式的两边都减2,不等号的方向不变,故A错误;
B、不等式的两边都除以2,不等号的方向不变,故B错误;
C、如m=2,n=3,m>n,m2>n2,故C正确;
D、不等式的两边都乘以2,不等号的方向不变;不等式的两边都加2,不等号的方向不变;故D错误;
故选:C.
6.已知菱形的周长为40cm,两条对角线之比3:4,则菱形面积为( )
A.962
B.48cm2
C.24cm2
D.12cm2
【考点】L8:菱形的性质.
【分析】设菱形的对角线分别为3a,4a,列出方程求出a2,根据菱形的面积=×3a×4a=6a2即可解决问题.
【解答】解:设菱形的对角线分别为3a,4a,
∵菱形的周长为40,
∴菱形的边长为10,
∴()2+(2a)2=102,
∴a2=16,
∴菱形的面积=×3a×4a=6a2=96.
故选A.
7.x的2倍减去7的差不大于﹣1,可列关系式为( )
A.2x﹣7≤﹣1
B.2x﹣7<﹣1
C.2x﹣7=﹣1
D.2x﹣7≥﹣1
【考点】C8:由实际问题抽象出一元一次不等式.
【分析】理解:不大于﹣1,即是小于或等于﹣1.
【解答】解:根据题意,得
2x﹣7≤﹣1.
故选:A.
8.已知:线段AB,BC,∠ABC=90°.求作:矩形ABCD.
以下是甲、乙两同学的作业:
甲:
1.以点C为圆心,AB长为半径画弧;
2.以点A为圆心,BC长为半径画弧;
3.两弧在BC上方交于点D,连接AD,CD,四边形ABCD即为所求(如图1).
乙:
1.连接AC,作线段AC的垂直平分线,交AC于点M;
2.连接BM并延长,在延长线上取一点D,使MD=MB,连接AD,CD,四边形ABCD即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
【考点】N3:作图—复杂作图;LC:矩形的判定.
【分析】先由两组对边分别相等的四边形是平行四边形得出四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形判断甲的作业正确;
先由对角线互相平分的四边形是平行四边形得出四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形判断乙的作业也正确.
【解答】解:由甲同学的作业可知,CD=AB,AD=BC,
∴四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴ ABCD是矩形.
所以甲的作业正确;
由乙同学的作业可知,CM=AM,MD=MB,
∴四边形ABCD是平行四边形,
又∵∠ABC=90°,
∴ ABCD是矩形.
所以乙的作业正确;
故选:A.
9.下列说法正确的是( )
A.﹣9的立方根是﹣3
B.±7是49的平方根
C.有理数与数轴上的点一一对应
D.算术平方根是9
【考点】29:实数与数轴;22:算术平方根;24:立方根.
【分析】根据开方运算,可得答案.
【解答】解:﹣9的立方根是,故A不符合题意;
B、±7是49的平方根,故B符合题意;
C、实数与数轴上的点一一对应,故C不符合题意;
D、算术平方根是3,故D不符合题意;
故选:B.
10.关于x的不等式组的解集为x>1,则a的取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
【考点】C3:不等式的解集.
【分析】解两个不等式后,根据其解集得出关于a的不等式,解答即可.
【解答】解:因为不等式组的解集为x>1,
所以可得a≤1,
故选D
11.如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A.72
B.52
C.80
D.76
【考点】KR:勾股定理的证明.
【分析】由题意∠ACB为直角,利用勾股定理求得外围中一条边,又由AC延伸一倍,从而求得风车的一个轮子,进一步求得四个.
【解答】解:依题意,设“数学风车”中的四个直角三角形的斜边长为x,则
x2=122+52=169
所以x=13
所以“数学风车”的周长是:(13+6)×4=76.
故选:D.
12.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF,则下列结论:①①△EBF≌△DFC;②四边形AEFD为平行四边形;③当AB=AC时,四边形AEFD是菱形;④当∠BAC=90°时,四边形AEFD是矩形.其中正确的结论有( )个.
A.1
B.2
C.3
D.4
【考点】LC:矩形的判定;KD:全等三角形的判定与性质;KK:等边三角形的性质;L7:平行四边形的判定与性质;LA:菱形的判定与性质.
【分析】①由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;
②利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;
③当AE=AD时,ADFE是菱形,可以用邻边相等的平行四边形是菱形判断即可;
④当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形,由此即可判断;
【解答】解:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
.
∴△EBF≌△DFC(SAS),故①正确,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形;故②正确,
若AB=AC,则AE=AD,四边形AEFD是菱形此,
故△ABC满足AB=AC时,四边形AEFD是菱形;故③正确
若∠BAC=150°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°﹣60°﹣60°﹣90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
∴∠BAC=120°,四边形AEFD不是矩形;故④错误,
故选C.
二、填空题(每小题3分,共15分)
13.若2m﹣1没有平方根,则m的取值范围是 m< .
【考点】21:平方根.
【分析】根据平方根的定义可知2m﹣1<0,解不等式即可.
【解答】解:∵负数没有平方根,
∴2m﹣1<0,
解得:m.
故答案为:m.
14.如图,A,B两地被一座小山阻隔,为测量A,B两地之间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB的中点D、E,测得DE的长度为360米,则A、B两地之间的距离是 720 米.
【考点】KX:三角形中位线定理.
【分析】首先根据D、E分别是CA,CB的中点,可得DE是△ABC的中位线,然后根据三角形的中位线定理,可得DE∥AB,且DE=,再根据DE的长度为360米,求出A、B两地之间的距离是多少米即可.
【解答】解:∵D、E分别是CA,CB的中点,
∴DE是△ABC的中位线,
∴DE∥AB,且DE=,
∵DE=360(米),
∴AB=360×2=720(米).
即A、B两地之间的距离是720米.
故答案为:720.
15.比较大小﹣6 < .
【考点】2A:实数大小比较.
【分析】求出=6,根据实数的大小比较法则比较即可.
【解答】解:∵=6,
∴﹣6<﹣,
故答案为:<.
16.如图,在网格图中的小正方形边长为1,则图中的△ABC的面积等于 5 .
【考点】K3:三角形的面积.
【分析】利用△ABC所在的矩形的面积减去四周三个直角三角形的面积列式计算即可得解.
【解答】解:△ABC的面积=3×4﹣×2×4﹣×1×3﹣×1×3
=12﹣4﹣1.5﹣1.5
=12﹣7
=5.
故答案为:5.
17.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是 (﹣4,3),或(﹣1,3),或(﹣9,3) .
【考点】LB:矩形的性质;D5:坐标与图形性质;KI:等腰三角形的判定;KQ:勾股定理.
【分析】先由矩形的性质求出OD=5,分情况讨论:(1)当OP=OD=5时;根据勾股定理求出PC,即可得出结果;
(2)当PD=OD=5时;①作PE⊥OA于E,根据勾股定理求出DE,得出PC,即可得出结果;
②作PF⊥OA于F,根据勾股定理求出DF,得出PC,即可得出结果.
【解答】解:∵A(﹣10,0),C(0,3),
∴OA=10,OC=3,
∵四边形OABC是矩形,
∴BC=OA=10,AB=OC=3,
∵D是OA的中点,
∴AD=OD=5,
分情况讨论:
(1)当OP=OD=5时,根据勾股定理得:PC==4,
∴点P的坐标为:(﹣4,3);
(2)当PD=OD=5时,分两种情况讨论:
①如图1所示:作PE⊥OA于E,
则∠PED=90°,DE==4,
∴PC=OE=5﹣4=1,
∴点P的坐标为:(﹣1,3);
②如图2所示:作PF⊥OA于F,
则DF==4,
∴PC=OF=5+4=9,
∴点P的坐标为:(﹣9,3);
综上所述:点P的坐标为:(﹣4,3),或(﹣1,3),或(﹣9,3);
故答案为:(﹣4,3),或(﹣1,3),或(﹣9,3).
三、解答题(本题共8小题,共69分)
18.(1)﹣+
(2)|1﹣|+|﹣|+|﹣2|
【考点】2C:实数的运算.
【分析】(1)首先计算开方,然后从左向右依次计算,求出算式的值是多少即可.
(2)根据绝对值的含义和求法,求出算式的值是多少即可.
【解答】解:(1)﹣+
=5﹣(﹣3)+0.5
=8+0.5
=8.5
(2)|1﹣|+|﹣|+|﹣2|
=﹣1+﹣+2﹣
=1
19.解不等式或不等式组.
(1)4x+5≥6x﹣3.并将解集在数轴上表示出来;
(2).
【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集;C6:解一元一次不等式.
【分析】(1)移项,合并同类项,最后把不等式的解集在数轴上表示出来即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
【解答】解:(1)4x﹣6x≥﹣3﹣5,
﹣2x≥﹣8,
x≤4;
将解集在数轴上表示出来为:
(2),
由不等式①得:x≥1,
由不等式②得:x<4.
故不等式组的解集为1≤x<4.
20.已知2a﹣1的平方根是±3,3a+b﹣1的立方根是2,求2a﹣b的平方根.
【考点】21:平方根;24:立方根.
【分析】根据平方根和立方根得出2a﹣1=9,3a+b﹣1=8,求出a、b的值即可.
【解答】解:∵2a﹣1的平方根是±3,
∴2a﹣1=9,
a=5,
∵3a+b﹣1的立方根是2,
∴3a+b﹣1=8,
∴b=﹣6,
∴2a﹣b=16,
∴2a﹣b的平方根是±4.
21.如图,在 ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90°,求证:四边形DEBF是菱形.
【考点】L9:菱形的判定;L5:平行四边形的性质.
【分析】(1)根据已知条件证明BE=DF,BE∥DF,从而得出四边形DFBE是平行四边形,即可证明DE∥BF,
(2)先证明DE=BE,再根据邻边相等的平行四边形是菱形,从而得出结论.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵点E、F分别是AB、CD的中点,
∴BE=AB,DF=CD.
∴BE=DF,BE∥DF,
∴四边形DEBF是平行四边形,
∴DE∥BF;
(2)∵∠G=90°,AG∥BD,AD∥BG,
∴四边形AGBD是矩形,
∴∠ADB=90°,
在Rt△ADB中
∵E为AB的中点,
∴AE=BE=DE,
∵四边形DEBF是平行四边形,
∴四边形DEBF是菱形.
22.为提高饮水质量,越来越多的居民选购家用净水器,一商场抓住商机,从厂家购进了A,B两种型号家用净水器,其数量和进价如表:
型号
数量(台)
进价(元/台)
A
10
150元
B
5
350元
为使每台B型号家用净水器的售价是A型号的2倍,且保证售完这批家用净水器的利润不低于1650元,每台A型号家用净水器的售价至少应为多少元?(注:利润=售价﹣进价)
【考点】C9:一元一次不等式的应用.
【分析】设每台A型号家用净水器的售价为x元,则每台B型号家用净水器的售价是2x元,根据售完这批家用净水器的利润不低于1650元,列出不等式解答即可.
【解答】解:设每台A型家用净水器售价为x元,根据题意可得:
10(x﹣150)+5(2x﹣350)≥1650,
解得:x≥245,
故x的最小值为245,
答:每台A型号家用净水器的售价至少245元.
23.甲、乙两船从位于南北走向的海岸线上的港口A同时出发,甲以每小时15海里的速度向北偏东40°方向航行,乙船以每小时20海里的速度向另一方向航行,4小时后甲船到达C岛,乙船到达B岛,已知B、C两岛相距100海里,判断乙船航行的方向,并说明理由.
【考点】KU:勾股定理的应用;KS:勾股定理的逆定理.
【分析】根据题意得出AC,AB的长,再利用勾股定理的逆定理得出△BAC是直角三角形,进而得出答案.
【解答】解:由题意可得:
AC=15×4=60(海里),
AB=20×4=80(海里),
AC2+AB2=602+802=10000,
BC2=10000,
故AC2+AB2=BC2,
∴△BAC是直角三角形,
∴∠BAC=90°,
180°﹣40°﹣90°=50°,
∴乙船航行的方向是南偏东50°(或东偏南40°).
24.对于实数x,符号[x]表示不大于x的最大整数解,如:[π]=3,[6]=6,[﹣7.5]=﹣8.
(1)若[a]=﹣3,那么a的取值范围是 ﹣3≤a<﹣2 ;
(2)若[]=2,求满足条件的所有正整数a.
【考点】CE:一元一次不等式组的应用.
【分析】(1)根据[a]=﹣3,得出﹣3≤a<﹣2,求出a的取值范围即可;
(2)根据题意得出2≤<3,求出x的取值范围,从而得出满足条件的所有正整数的解.
【解答】解:(1)∵[a]=﹣3,
∴a的取值范围是﹣3≤a<﹣2;
故答案为:﹣3≤a<﹣2.
(2)根据题意得:
2≤<3,
解得:2≤x<5,
∵为正整数,
∴a=2,3,4.
则满足条件的所有正整数a为2,3,4.
25.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【考点】LE:正方形的性质;KD:全等三角形的判定与性质;L8:菱形的性质.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
2017年5月29日
同课章节目录
