山东省济宁市高新区2017年九年级下册第二次质量检测数学试题(含答案)
文档属性
| 名称 | 山东省济宁市高新区2017年九年级下册第二次质量检测数学试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 305.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-31 18:37:08 | ||
图片预览


文档简介
2016—2017学年度九年级第二次质量检测
数
学
试
题
题号
一
二
三
总分
16
17
18
19
20
21
22
得分
选择题答题栏
题
号
1
2
3
4
5
6
7
8
9
10
答
案
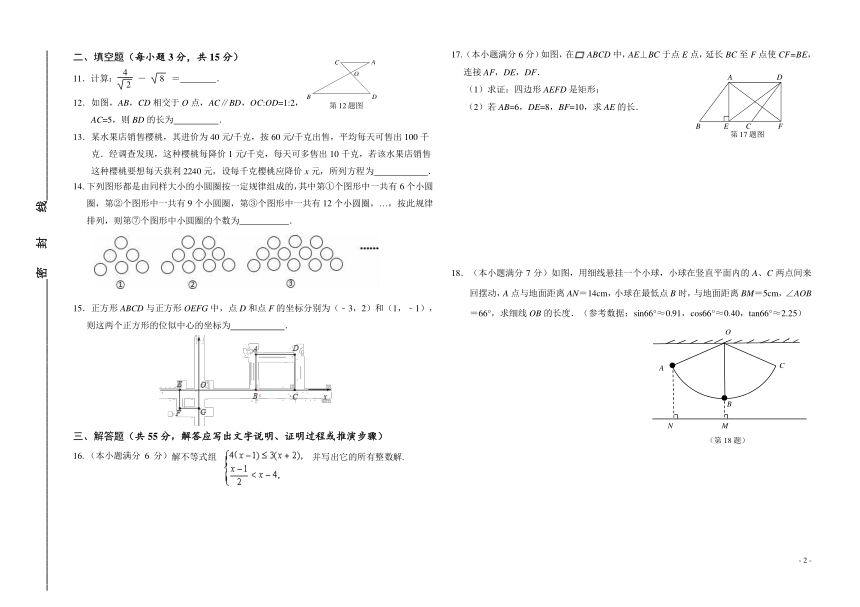
一、选择题(各小题的四个选项中,只有一项符合题意,每小题3分,共30分)
1.
下列各对数是互为倒数的是
A.4和﹣4
B.﹣3和
C.﹣2和
D.0和0
2.
下列图案中
,既是中心对称又是轴对称图形的是
A
B
C
D
3.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是
A
B
C
D
4.初三(8)班体委用划记法统计本班40名同学投掷实心球的成绩,结果如下表所示:
则这40名同学投掷实心球的成绩的众数和中位数分别是
A.8,8.5
B.9,8.5
C.8,8
D.9,8
5.如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2
的度数为
A.35°
B.15°
C.10°
D.5°
6.用配方法解方程x2﹣4x﹣1=0,方程应变形为
A.
B.
C.
D.
7.如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=50°,则∠B的度数为
A.60°
B.50°
C.40°
D.30°
8.若+|2a﹣b+1|=0,则(b﹣a)2017等于
A.﹣1
B.1
C.52017
D.﹣52017
9.
如图,△ABC三个顶点分别在反比例函数y=,y=的图像上,若∠C=90°,
AC∥y
轴,BC∥x
轴,S△ABC=8,则k的值为
A.3
B.5
C.6
D.4
10.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E
为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的
最小值是
A.
B.
3
C.
2
D.
二、填空题(每小题3分,共15分)
11.计算:
EQ
\F(
4
,)
-
=
.
12.如图,AB,CD相交于O点,AC∥BD,OC:OD=1:2,
AC=5,则BD的长为
.
13.某水果店销售樱桃,其进价为40元/千克,按60元/千克出售,平均每天可售出100千
克.经调查发现,这种樱桃每降价1元/千克,每天可多售出10千克,若该水果店销售
这种樱桃要想每天获利2240元,设每千克樱桃应降价x元,所列方程为
.
14.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆
圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律
排列,则第⑦个图形中小圆圈的个数为
.
15.正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),
则这两个正方形的位似中心的坐标为 .
三、解答题(共55分,解答应写出文字说明、证明过程或推演步骤)
16.(本小题满分6分)解不等式组并写出它的所有整数解.
17.(本小题满分6分)如图,在ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
18.(本小题满分7分)如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
19.(本小题满分8分)为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行
科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类
别的比赛),各类别参赛人数统计如图:
请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类
一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取
1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是
多少?
20.
(本小题满分8分)如图,四边形ABCD内接于⊙O,且BD为直径,∠,
过A点的AC的垂线交CB的延长线于点E.
(1)求证:BE=CD;
(2)如果AD=,求图中阴影的面积.
21.(本小题满分9分)有这样一个问题:探究函数的图象与性质.
下面是小文的探究过程,请补充完整:
(1)函数的自变量x的取值范围是
;
(2)下表是y与x的几组对应值.
x
…
0
2
3
4
5
…
y
…
0
2
…
如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点和,和,和,和均关于某点中心对称,则该点的坐标为
;
②小文分析函数的表达式发现:当时,该函数的最大值为0,则该函数图象在直线左侧的最高点的坐标为
;
(3)小文补充了该函数图象上两个点(),(),
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:________________
.
22.(本小题满分11分)如图,已知抛物线y=﹣x2+2x的顶点为A,直线y=x﹣2与抛物线
交于B,C两点.
(1)求A,B,C三点的坐标;
(2)作CD⊥轴于点D,求证:△ODC∽△ABC;
(3)若点P为抛物线上的一个动点,过点P作PM⊥轴于点M,则是否还存在除C
点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请
求出这样的P点坐标;若不存在,请说明理由.
2016—2017学年度九年级第二次质量检测
数学试题评分标准与参考答案
一、选择题
1.C
2.
A
3.B
4.D
5.C
6.D
7.C
8.
A
9.B
10.
D
二、填空题
11.0
12.
10
13.
(60-x-40)(100+10x)
=
2240
14.
24
15.
(﹣1,0)或(5,﹣2).
三、解答题
16.
解:解不等式①,得
.
解不等式②,得 .
∴
原不等式组的解集为.
∴
原不等式组的所有整数解为8,9,10.
17.
(1)证明:∵
CF=BE,
∴
CF+EC=BE+EC.
即
EF=BC.
∵
在ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD
=
EF.
∴
四边形AEFD是平行四边形.
∵
AE⊥BC,
∴
∠AEF=90°.
∴
AEFD是矩形.
(2)解:
∵
AEFD是矩形,DE=8,
∴
AF=DE=8.
∵
AB=6,BF=10,
∴
.
∴
∠BAF=90°.
∵
AE⊥BF,
∴
.
∴
.
18.
解:过点A作AD⊥OB于点D.
由题意得AN⊥MN,OB⊥MN,AD⊥OB,∴四边形ANMD是矩形,
∴DM=AN,
设OB=OA=x
cm,在Rt OAD中,∠ODA=90°,
cos∠AOD=
=
≈0.6.
解得x=15cm.
经检验,x=15为原方程的解.
答:细线OB的长度是15cm.
19.
(1)
60
72
;
(2)
环保15人,建模12人.图略
(3)
概率为,树状图略.
20.(1)(4分)(证明过程略);
(2)(4分,解答过程略)阴影的面积为.
21.(1)(2分);
(2)(4分)①(1,1);
②(0,0);
(3)①(2分)如右图;
②(1分)该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
(ⅳ)当x>1时,该函数的最小值为1.
……
(写出一条即可)
22.(1)(3分)略解:∵,
∴A为(1,1).
解得或.
∴B(2,0),C(﹣1,﹣3).
(2)(4分)(证明过程略)
提示:证,.
(3)(4分)存在这样的P点;(证明过程略)
提示:设M为(,0),则P为(,).
∴,.
当以O,P,M为顶点的三角形与△ABC相似时,
有或.
而可求得,.
①当时,代入解得:或.
②当时,代入解得:或(舍去).
所以,存在这样的点,坐标为(,0)或(,0)或(5,0).
____________________________________________________密
封
线_________________________
姓名___________学校___________班级_________考号___________
第5题图
x
O
A
B
C
(第9题)
第10题图
第7题图
第12题图
____________________________________________________密
封
线_________________________
第17题图
A
B
M
N
C
O
(第18题)
____________________________________________________密
封
线_________________________
O
第20题图
A
C
B
D
E
____________________________________________________密
封
线_________________________
x=1
第22题图
A
B
M
N
C
O
D
PAGE
-
6
-
数
学
试
题
题号
一
二
三
总分
16
17
18
19
20
21
22
得分
选择题答题栏
题
号
1
2
3
4
5
6
7
8
9
10
答
案
一、选择题(各小题的四个选项中,只有一项符合题意,每小题3分,共30分)
1.
下列各对数是互为倒数的是
A.4和﹣4
B.﹣3和
C.﹣2和
D.0和0
2.
下列图案中
,既是中心对称又是轴对称图形的是
A
B
C
D
3.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是
A
B
C
D
4.初三(8)班体委用划记法统计本班40名同学投掷实心球的成绩,结果如下表所示:
则这40名同学投掷实心球的成绩的众数和中位数分别是
A.8,8.5
B.9,8.5
C.8,8
D.9,8
5.如图,等腰直角三角板的顶点A,C分别在直线a,b上.若a∥b,∠1=35°,则∠2
的度数为
A.35°
B.15°
C.10°
D.5°
6.用配方法解方程x2﹣4x﹣1=0,方程应变形为
A.
B.
C.
D.
7.如图,AB为⊙O的直径,点C在⊙O上,若∠ACO=50°,则∠B的度数为
A.60°
B.50°
C.40°
D.30°
8.若+|2a﹣b+1|=0,则(b﹣a)2017等于
A.﹣1
B.1
C.52017
D.﹣52017
9.
如图,△ABC三个顶点分别在反比例函数y=,y=的图像上,若∠C=90°,
AC∥y
轴,BC∥x
轴,S△ABC=8,则k的值为
A.3
B.5
C.6
D.4
10.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点F在边AC上,并且CF=2,点E
为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的
最小值是
A.
B.
3
C.
2
D.
二、填空题(每小题3分,共15分)
11.计算:
EQ
\F(
4
,)
-
=
.
12.如图,AB,CD相交于O点,AC∥BD,OC:OD=1:2,
AC=5,则BD的长为
.
13.某水果店销售樱桃,其进价为40元/千克,按60元/千克出售,平均每天可售出100千
克.经调查发现,这种樱桃每降价1元/千克,每天可多售出10千克,若该水果店销售
这种樱桃要想每天获利2240元,设每千克樱桃应降价x元,所列方程为
.
14.下列图形都是由同样大小的小圆圈按一定规律组成的,其中第①个图形中一共有6个小圆
圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律
排列,则第⑦个图形中小圆圈的个数为
.
15.正方形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),
则这两个正方形的位似中心的坐标为 .
三、解答题(共55分,解答应写出文字说明、证明过程或推演步骤)
16.(本小题满分6分)解不等式组并写出它的所有整数解.
17.(本小题满分6分)如图,在ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
18.(本小题满分7分)如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
19.(本小题满分8分)为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行
科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类
别的比赛),各类别参赛人数统计如图:
请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类
一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取
1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是
多少?
20.
(本小题满分8分)如图,四边形ABCD内接于⊙O,且BD为直径,∠,
过A点的AC的垂线交CB的延长线于点E.
(1)求证:BE=CD;
(2)如果AD=,求图中阴影的面积.
21.(本小题满分9分)有这样一个问题:探究函数的图象与性质.
下面是小文的探究过程,请补充完整:
(1)函数的自变量x的取值范围是
;
(2)下表是y与x的几组对应值.
x
…
0
2
3
4
5
…
y
…
0
2
…
如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.
①观察图中各点的位置发现:点和,和,和,和均关于某点中心对称,则该点的坐标为
;
②小文分析函数的表达式发现:当时,该函数的最大值为0,则该函数图象在直线左侧的最高点的坐标为
;
(3)小文补充了该函数图象上两个点(),(),
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:________________
.
22.(本小题满分11分)如图,已知抛物线y=﹣x2+2x的顶点为A,直线y=x﹣2与抛物线
交于B,C两点.
(1)求A,B,C三点的坐标;
(2)作CD⊥轴于点D,求证:△ODC∽△ABC;
(3)若点P为抛物线上的一个动点,过点P作PM⊥轴于点M,则是否还存在除C
点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请
求出这样的P点坐标;若不存在,请说明理由.
2016—2017学年度九年级第二次质量检测
数学试题评分标准与参考答案
一、选择题
1.C
2.
A
3.B
4.D
5.C
6.D
7.C
8.
A
9.B
10.
D
二、填空题
11.0
12.
10
13.
(60-x-40)(100+10x)
=
2240
14.
24
15.
(﹣1,0)或(5,﹣2).
三、解答题
16.
解:解不等式①,得
.
解不等式②,得 .
∴
原不等式组的解集为.
∴
原不等式组的所有整数解为8,9,10.
17.
(1)证明:∵
CF=BE,
∴
CF+EC=BE+EC.
即
EF=BC.
∵
在ABCD中,AD∥BC且AD=BC,
∴AD∥EF且AD
=
EF.
∴
四边形AEFD是平行四边形.
∵
AE⊥BC,
∴
∠AEF=90°.
∴
AEFD是矩形.
(2)解:
∵
AEFD是矩形,DE=8,
∴
AF=DE=8.
∵
AB=6,BF=10,
∴
.
∴
∠BAF=90°.
∵
AE⊥BF,
∴
.
∴
.
18.
解:过点A作AD⊥OB于点D.
由题意得AN⊥MN,OB⊥MN,AD⊥OB,∴四边形ANMD是矩形,
∴DM=AN,
设OB=OA=x
cm,在Rt OAD中,∠ODA=90°,
cos∠AOD=
=
≈0.6.
解得x=15cm.
经检验,x=15为原方程的解.
答:细线OB的长度是15cm.
19.
(1)
60
72
;
(2)
环保15人,建模12人.图略
(3)
概率为,树状图略.
20.(1)(4分)(证明过程略);
(2)(4分,解答过程略)阴影的面积为.
21.(1)(2分);
(2)(4分)①(1,1);
②(0,0);
(3)①(2分)如右图;
②(1分)该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
(ⅳ)当x>1时,该函数的最小值为1.
……
(写出一条即可)
22.(1)(3分)略解:∵,
∴A为(1,1).
解得或.
∴B(2,0),C(﹣1,﹣3).
(2)(4分)(证明过程略)
提示:证,.
(3)(4分)存在这样的P点;(证明过程略)
提示:设M为(,0),则P为(,).
∴,.
当以O,P,M为顶点的三角形与△ABC相似时,
有或.
而可求得,.
①当时,代入解得:或.
②当时,代入解得:或(舍去).
所以,存在这样的点,坐标为(,0)或(,0)或(5,0).
____________________________________________________密
封
线_________________________
姓名___________学校___________班级_________考号___________
第5题图
x
O
A
B
C
(第9题)
第10题图
第7题图
第12题图
____________________________________________________密
封
线_________________________
第17题图
A
B
M
N
C
O
(第18题)
____________________________________________________密
封
线_________________________
O
第20题图
A
C
B
D
E
____________________________________________________密
封
线_________________________
x=1
第22题图
A
B
M
N
C
O
D
PAGE
-
6
-
同课章节目录
