2017年河北省献县垒头中学 12.1 杠杆 同步练习(含答案)
文档属性
| 名称 | 2017年河北省献县垒头中学 12.1 杠杆 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.4KB | ||
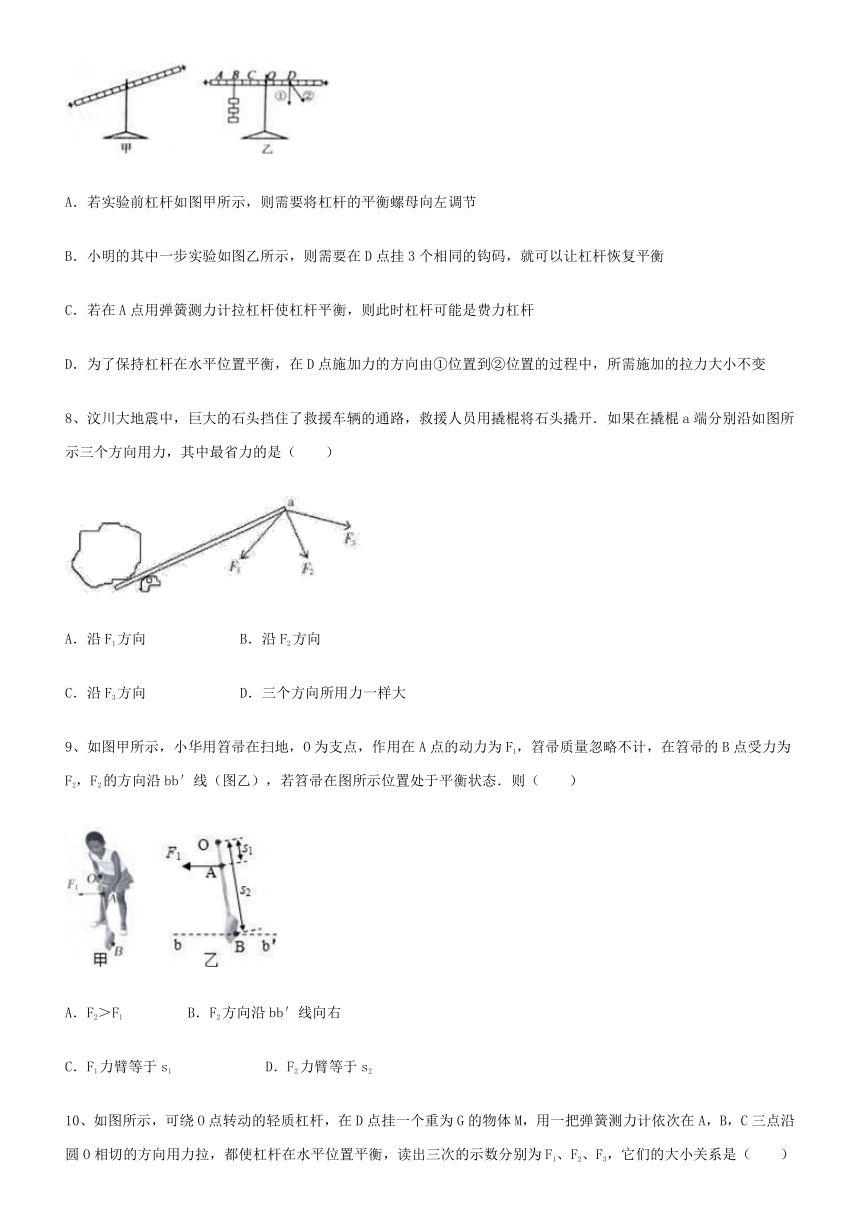
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-06-01 00:00:00 | ||
图片预览


文档简介
2017年河北省献县垒头中学
12.1
杠杆练习
选择题
1、图中正在使用的机械,属于费力杠杆的有( )
A.①③
B.②③
C.①④
D.②④
2、如图所示,OAB为轻质杠杆,可绕支点O自由转动,在B端施加一个动力使杠杆在水平位置平衡,该杠杆( )
A.一定是省力杠杆
B.一定是费力杠杆
C.一定是等臂杠杆
D.以上情况都有可能
3、如图所示,活塞式抽水机手柄可以看做是绕O点转动的杠杆.它在动力F1和阻力F2的作用下,处于平衡状态,要想最省力应使F1沿着那个方向?( )
A.由C指向F
B.由C指向D
C.由C指向E
D.由C指向O
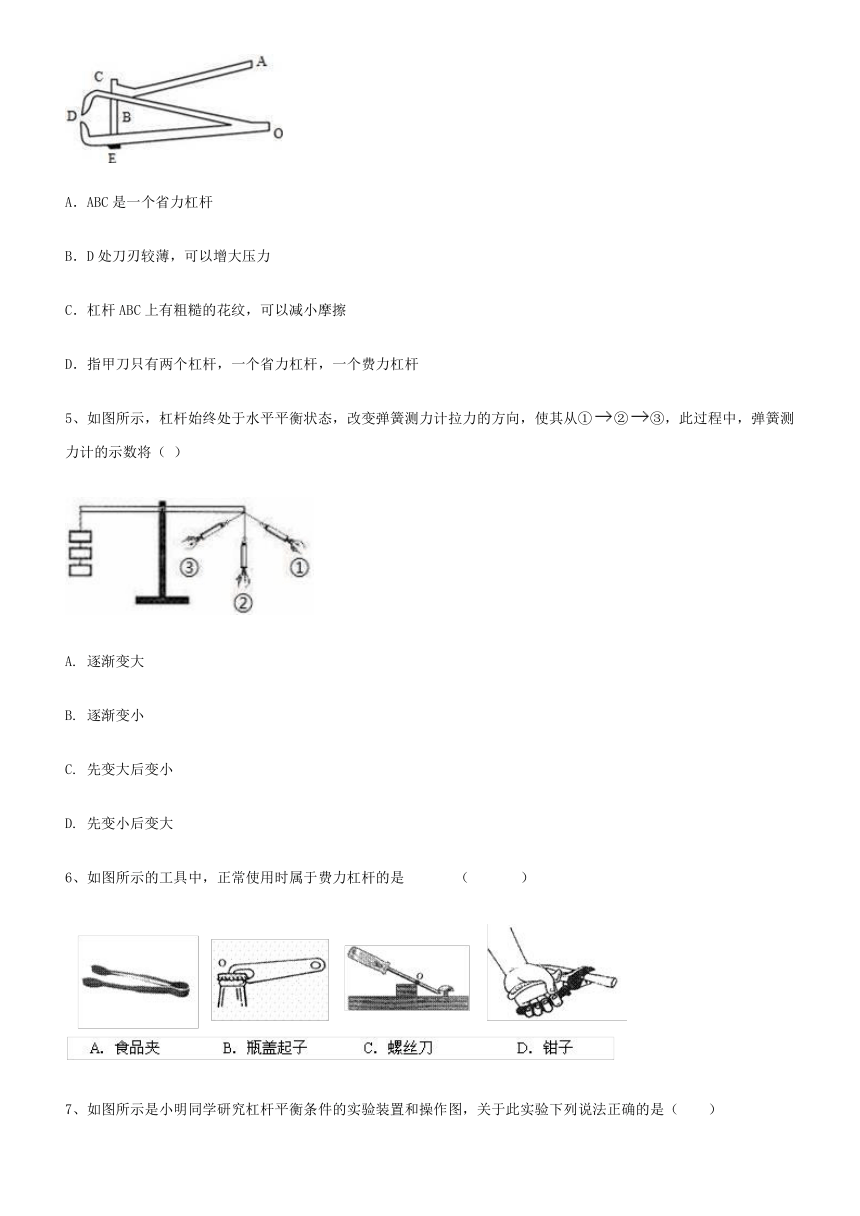
4、如图所示,是一种指甲刀的结构示意图,下列说法正确的是( )
A.ABC是一个省力杠杆
B.D处刀刃较薄,可以增大压力
C.杠杆ABC上有粗糙的花纹,可以减小摩擦
D.指甲刀只有两个杠杆,一个省力杠杆,一个费力杠杆
5、如图所示,杠杆始终处于水平平衡状态,改变弹簧测力计拉力的方向,使其从①②③,此过程中,弹簧测力计的示数将(
)
A.
逐渐变大
B.
逐渐变小
C.
先变大后变小
D.
先变小后变大
6、如图所示的工具中,正常使用时属于费力杠杆的是
(
)
7、如图所示是小明同学研究杠杆平衡条件的实验装置和操作图,关于此实验下列说法正确的是( )
A.若实验前杠杆如图甲所示,则需要将杠杆的平衡螺母向左调节
B.小明的其中一步实验如图乙所示,则需要在D点挂3个相同的钩码,就可以让杠杆恢复平衡
C.若在A点用弹簧测力计拉杠杆使杠杆平衡,则此时杠杆可能是费力杠杆
D.为了保持杠杆在水平位置平衡,在D点施加力的方向由①位置到②位置的过程中,所需施加的拉力大小不变
8、汶川大地震中,巨大的石头挡住了救援车辆的通路,救援人员用撬棍将石头撬开.如果在撬棍a端分别沿如图所示三个方向用力,其中最省力的是( )
A.沿F1方向
B.沿F2方向
C.沿F3方向
D.三个方向所用力一样大
9、如图甲所示,小华用笤帚在扫地,O为支点,作用在A点的动力为F1,笤帚质量忽略不计,在笤帚的B点受力为F2,F2的方向沿bb′线(图乙),若笤帚在图所示位置处于平衡状态.则( )
A.F2>F1
B.F2方向沿bb′线向右
C.F1力臂等于s1
D.F2力臂等于s2
10、如图所示,可绕O点转动的轻质杠杆,在D点挂一个重为G的物体M,用一把弹簧测力计依次在A,B,C三点沿圆O相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为F1、F2、F3,它们的大小关系是( )
A.F1<F2<F3<G
B.F1>F2>F3>G
C.F1=F2=F3=G
D.F1>F2=F3=G
11、有一种多功能剪刀,如图所示,图中标注了该剪刀的相关用途.对于它的使用,以下分析正确的是( )
A.做为剪刀使用时:物体越靠近O点越省力
B.做为启瓶器使用时:它是一个费力杠杆
C.做为削皮刀使用时:刀刃很锋利,是为了增大压力把果皮削掉
D.做为挤压钳使用时:挤压齿尖锐,是为了减小压强把果壳挤开
12、如图所示为等刻度轻质杠杆,A处挂2牛的物体,若使杠杆在水平位置平衡,则在B处施加的力( )
A.可能为0.5牛
B.一定为1牛
C.可能为2牛
D.一定是4牛
13、如图是人抬独轮车车把时的简化示意图,此时独轮车相当一个______杠杆;若动力臂是阻力臂的3倍,物体和车总重G为1200N,则抬起车把的力F为______N.
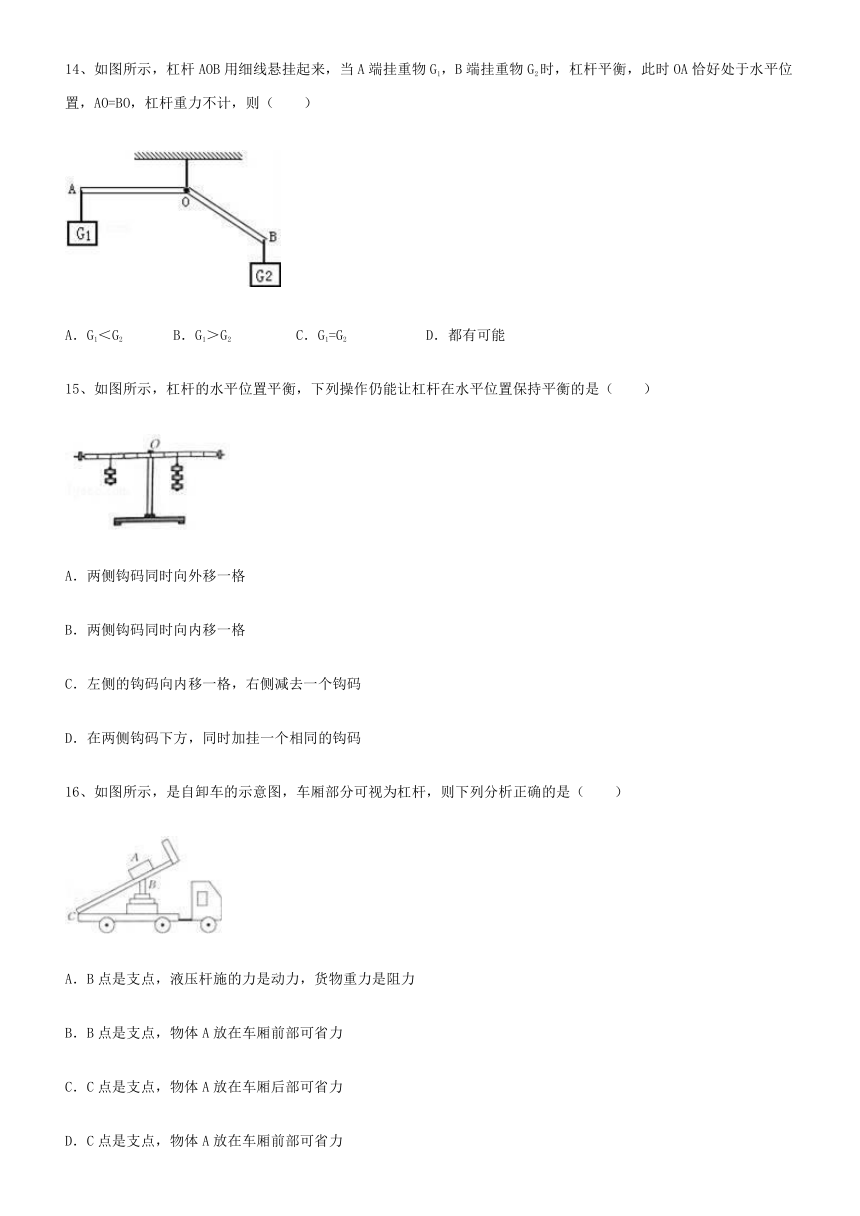
14、如图所示,杠杆AOB用细线悬挂起来,当A端挂重物G1,B端挂重物G2时,杠杆平衡,此时OA恰好处于水平位置,AO=BO,杠杆重力不计,则( )
A.G1<G2
B.G1>G2
C.G1=G2
D.都有可能
15、如图所示,杠杆的水平位置平衡,下列操作仍能让杠杆在水平位置保持平衡的是( )
A.两侧钩码同时向外移一格
B.两侧钩码同时向内移一格
C.左侧的钩码向内移一格,右侧减去一个钩码
D.在两侧钩码下方,同时加挂一个相同的钩码
16、如图所示,是自卸车的示意图,车厢部分可视为杠杆,则下列分析正确的是( )
A.B点是支点,液压杆施的力是动力,货物重力是阻力
B.B点是支点,物体A放在车厢前部可省力
C.C点是支点,物体A放在车厢后部可省力
D.C点是支点,物体A放在车厢前部可省力
17、在质量可忽略的杠杆的A、B两端各挂有体积相同的铜块和铝块(ρ铜>ρ铝),支点O在如图所示的位置时,杠杆在水平位置保持平衡.在下列情况下,杠杆仍然在水平位置保持平衡的是( )
A.在铜块和铝块上各加一块质量相等的物体
B.将铜块和铝块同时向支点移动一小段相同的距离
C.将铜块和铝块各切去体积相同的一小部分
D.将铜块和铝块同时浸没在水中
18、如图所示,杠杆上分别放着质量不相等的两个球,杠杆在水平位置平衡,如果两球以相同速度同时匀速向支点移动,则杠杆( )
A.仍能平衡
B.不能平衡,大球那端下沉
C.不能平衡,小球那端下沉
D.无法判断
19、一根轻质杠杆,在左右两端分别挂在300牛的铜块和200牛的铝块时,杠杆恰好平衡.若将两边物重同时减少50牛,则杠杆( )
A.左端下沉
B.右端下沉
C.仍然平衡
D.无法确定
20、前不久,台风“卡努”经过常州,吹倒了一些树木,园林工人在扶正被风吹倒的树木后,还用绳索牵拉固定(绳的一端绑在木桩上),如图所示,则下列措施最合适的是( )
A.绳的另一端系在A点
B.绳的另一端系在B点
C.在A点垫上木板,再系上绳
D.在B点垫上木板,再系上绳
21、如如图所示杠杆,O是支点,中间挂一重物G,如果在杠杆的另一端M处加一个力F使杠杆平衡,且要求所加的力要最小,则这个力( )
A.应沿MQ方向
B.应沿MP方向
C.应沿MN方向
D.可沿任意方向
二、填空题
22、如图,轻杆OA可绕O点自由转动,用细线将15N的重物挂在A处,小林在B处用竖直向上的拉力提住轻杆,OB和BA长度之比为3:5,下列问题中,轻杆始终在水平位置处于平衡.
(1)此杠杆类型与 相同(选填“钓鱼竿”或“羊角锤”);
(2)拉力大小为 N;
(3)若仅增加物重,则拉力的变化量与物重的变化量之比为 ;
(4)若拉力方向变为图中虚线所示方向,则拉力将变 .
23、在一轻质杠杆的两端分别挂上质量不等的两个铁块M1、M2(M1>M2),调节两物体到支点的距离,使杠杆平衡,则 (选填“M1”或“M2”)离支点较远些.然后将物体同时浸没在水中,杠杆 (选填“能”或“不能”)保持平衡.
24、如图所示,重为10N的物体G挂在杠杆的A端(杠杆重力不计),要使杠杆在图示位置平衡,在B端至少要施加 N的力,力的方向是 .
25、轻质木棒
AB
可以绕
O
点转动,OA
:
OB
=
3
:
1,A
端细线下挂
300N
的重物静止在水平地面上,若使木杆保持水平位置,且重物对水平地面的压力为零,在
B
点要用_____N的力竖直向下拉,此时木棒为_____(省力/费力/等臂)杠杆。
26、如图为水平桌面上的圆形玻璃转盘(转盘半径为50cm),在水平力作用下能绕转盘中心O点自由转动,转动时可视为杠杆.甲在A点施加一个大小为20N的水平力FA,想让转盘转动,对面的乙在距O点40cm处的B点同时施加一个水平力,想让转盘反方向转动,乙应沿图中 (选填“F1”、“F2”、“F3”或“F4”)方向施加一个至少为 N的力,才可能达到目的(假设只有甲、乙两人对转盘施力,忽略其它力对转动的影响).
27、如图所示,在已经处于水平位置平衡的杠杆的A点悬挂两个总重为2N的钩码,在B点用弹簧测力计竖直向上拉,使杠杆在水平位置再次平衡,则拉力应为 N,此时的杠杆属于 (选填“省力”或“费力”)杠杆.如果测力计的量程为0~5N,在支点不变的情况下,采用图中的杠杆,能较为精确地测量出悬挂物体的最大质量为 kg.(g取10N/kg)
三、实验,探究题
28、从地面上搬起重物我们的常见做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?下面就建立模型说明这个问题.把脊柱简化为杠杆如图丙所示,脊柱可绕骶骨(轴)O转动,腰背部复杂肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,在B点挂一重物代替箱子.用测力计沿F1方向拉,使模型静止,可测出腰背部复杂肌肉拉力的大小.接着,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论.
(1)当α角增大时,F2的力臂L2 (变大/不变/变小),F1 (变大/不变/变小).
(2)如果考虑到人上半身的重力,那么腰背部肌肉的实际拉力将比丙图中F1要 (大/小).
(3)对比甲乙两种姿势所对应丙图中的两种状态,由以下分析可得, (甲/乙)图中的姿势比较正确.
29、如图所示,是探究杠杆平衡条件的实验装置,已知杠杆上刻度均匀,每个钩码质量均为50g。
(1)将杠杆中点置于支架上,不挂钩码,当杠杆静止时,发现杠杆左端上翘.此时应将杠杆两端的平衡螺母向_______(选填“左”或“右”)调节,使杠杆在水平位置平衡;
(2)当凋节杠杆在水平平衡后,在A点悬挂两个钩码,要使杠杆在水平位置再次平衡,需在B点悬挂总重为_______N的钩码;
(3)撤去B点所挂钩码,改用弹簧测力计在C点竖直向上拉,使杠杆在水平位置平衡。若此时改变弹簧测力计拉力的方向,使之斜向左上方拉,杠杆仍然在水平位置平衡,则测力计的读数将_______
(选填“变大”、“不变”或“变小”)。
30、在“探究杠杆平衡条件的实验”中:
(1)如图甲所示,实验前,杠杆左端下沉,则应将左端的平衡螺母向 调节(选填“左”或“右”,直到杠杆在水平位置平衡,目的是便于测量 .
(2)如图乙所示,杠杆上的刻度均匀,在A点挂4个钩码,要使杠杆在水平位置平衡,应在B点挂 个相同的钩码;当杠杆平衡后,将A、B两点下方所挂的钩码同时朝远离支点O方向移动一小格,则杠杆 (选填“能”或”不能“)在水平位置保持平衡.
(3)如图丙所示,若不在B点挂钩码,改用弹簧测力计在B点向下拉杠杆,使杠杆仍在水平位置平衡,当测力计从a位置转动b位置时,其示数大小将 .
(4)如图丁所示,已知每个钩码重0.5N,杠杆上每小格长度为2cm,当弹簧测力计在C点斜向上拉(与水平方向成30°角)杠杆,使杠杆在水平位置平衡时,拉力F的力臂大小为 cm,弹簧测力计示数的大小为 N.
31、在探究杠杆平衡条件的实验中.
(1)如图a所示,要使杠杆在水平位置平衡,可将杠杆左端的平衡螺母向 调节.
(2)如图b所示,调节平衡后,左侧挂上钩码,在右侧用弹簧测力计(图中未画出)拉杠杆,使其在水平位置平衡,为便于测量力臂,应使弹簧测力计拉力的方向 .
(3)操作过程中,当弹簧测力计的示数达到量程仍不能使杠杆水平平衡,在不更换弹簧测力计的情况下,你认为接下来合理的操作是 .(写出一条即可)
(4)如图c所示,在A点挂上钩码,在B点用弹簧测力计竖直向上拉,使杠杆处于水平位置平衡,则此时弹簧测力计的示数是 N;将弹簧测力计逆时针转动60°,沿图示虚线方向拉,仍使杠杆在水平位置平衡,则弹簧测力计的示数将为 N.
参考答案
一、选择题
1、A【考点】杠杆的分类.
【分析】本题的解题关键是通过生活经验,体会支点的位置,判断出动力臂与阻力臂的长度关系,进而得出省力、费力情况.
【解答】解:①钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;
②羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆;
③筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;
④核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆.
综上所述,属于费力杠杆的有①③.
故选A.
2、D【考点】杠杆的分类.
【分析】使用杠杆时,如果动力臂大于阻力臂,为省力杠杆;如果动力臂等于阻力臂,为等臂杠杆;如果动力臂小于阻力臂,为费力杠杆;
因为在B点用力的方向不确定,所以其省费力情况要根据用力的方向确定.据此分析.
【解答】解:B点力的方向不同,力臂的大小则不同,不能确定动力臂与阻力臂的大小关系,所以此时杠杆可能省力,可能费力,可能既不省力也不费力.故ABC不符合题意,D符合题意.
故选D.
3、A【考点】杠杆中最小力的问题.
【分析】活塞式抽水机手柄可以看作是绕O点转动的杠杆,选项中的四个量应该分别代表了杠杆的动力、动力臂、阻力、阻力臂,关键是看它们的对应关系是否正确,据此来做出判断.
【解答】解:读图可知,F1为动力,其力臂是支点到动力作用线的垂直距离,此时力臂为OE;F2为阻力,其力臂是从支点到阻力作用线的垂直距离;
处于平衡状态,根据杠杆的平衡条件,要想最省力,力臂最长,应为OF,即F1沿着由C指向F方向,只有选项A符合题意.
故选A.
4、A【考点】杠杆的分类;摩擦力大小的影响因素;压强.
【分析】(1)对于杠杆类型的判断可从动力臂与阻力臂的大小关系上入手;
(2)压强的大小与压力的大小和受力面积的大小有关;
(3)滑动摩擦力的大小与压力的大小和接触面的粗糙程度有关.
【解答】解:A、对于ABC,如图所示,在使用时,它的动力臂大于阻力臂,所以它是省力杠杆,符合题意;
B、在相同的压力下,D处刀刃较薄,受力面积小,产生的压强大,压力的作用效果明显,并不是压力增大了,不符合题意;
C、杠杆ABC上有粗糙的花纹,增大接触面的粗糙程度,可以增大摩擦,不符合题意;
D、指甲刀中有三个杠杆:ABC、OBD、0ED,其中ABC是省力杠杆,其它两个都是费力杠杆,不符合题意.
故选A.
5、D
6、A
7、C【考点】杠杆的平衡条件.
【分析】(1)根据杠杆的平衡条件可知,杠杆倾斜时,杠杆的重心偏向杠杆下沉的一端,左、右两端的螺母(或一端的螺母)要向杠杆上翘的一端调节;
(2)根据杠杆的平衡条件分析解答;
(3)分析动力臂与阻力臂的大小,来确定是否为省力杠杆;
(4)由杠杆的平衡条件,在阻力阻力臂不变时,动力臂减小,动力变大.
【解答】解:
A、如图甲可知,杠杆左端下沉,则需要将平衡螺母向右调节,故A错误;
B、左侧力与力臂的乘积3G×4L=12GL;在D点挂3个相同钩码,右侧力与力臂的乘积3G×3L=9GL,左右两侧力与力臂的乘积不相等,故杠杆不平衡,B错误;
C、若在A点用弹簧测力计拉杠杆使杠杆平衡,由于没有明确力的方向,动力臂可能小于阻力臂,则此时杠杆可能是费力杠杆,故C正确;
D、为了保持杠杆在水平位置平衡,在D点施加力的方向由①位置到②位置的过程中,阻力和阻力臂不变,动力臂减小,由杠杆平衡条件可知,动力变大,故D错误.
故选C.
8、B
9、B
10、C【考点】杠杆的平衡条件.
【分析】利用杠杆平衡条件分析,当阻力和阻力臂不变时,如果动力臂不变,只改动用力方向,其动力不变,据此分析解答.
【解答】解:设拉力的力臂为L,则由题意可知,当杠杆在水平位置平衡时:G×OD=F×L
由此可得:F=
因为G,OD不变,OD=L=r,故F=G,由于F1、F2、F3的力臂都为圆的半径,相等,故F1=F2=F3=G
故选:C
11、A【考点】杠杆的应用;增大压强的方法及其应用.
【分析】多功能剪刀的不同部位有不同的用途,那是因为它的不同部位可以构成不同的简单机械或者是利用了不同的物理学原理.
【解答】解:A、做剪刀使用时:当所剪物体放在边缘时,动力臂小于阻力臂,是费力杠杆;当所剪物体放在靠里边时,动力臂大于阻力臂,是省力杠杆;当放在与动力臂相同的地方,是等臂杠杆,即不省力也不费力;所以物体越靠近O点越省力,故A正确;
B、做为启瓶器使用时,应用了杠杆的知识,动力臂大于阻力臂,是一个省力杠杆,故B错误.
C、做削皮刀使用时:刀刃很锋利,是在压力一定的条件下,减小接触面积增大压强,故C错误;
D、做挤压钳:应用了压强和摩擦力的知识.挤压齿尖且参差不齐,不仅通过减小受力面积的方法增大了压强;还通过增加表面粗糙程度的方法增大了摩擦力,既利于挤压果壳.又避免坚果滑落,故D错误;
12、C【考点】杠杆的平衡条件;杠杆中最小力的问题.
【分析】根据杠杆平衡的条件和杠杆中最小力的问题进行分析,即动力乘以动力臂等于阻力乘以阻力臂,支点与力的作用点的连线为最长力臂.
【解答】解:根据杠杆平衡的条件求出在B处施加最小的力为:
F1L1=F2L2
由题意可知,只有杠杆自重等不计,力的方向与杠杆垂直时,力的大小才是1N,但如果力的方向与杠杆不垂直,则力将会大于1N,即有可能是2N.
故选C.
13、【考点】杠杆的平衡分析法及其应用.
【分析】(1)根据动力臂与阻力臂的大小关系判断杠杆的类型.
(2)根据杠杆的平衡条件计算动力的大小.
【解答】解:(1)如图,抬独轮车车把时,动力臂L1大于阻力臂L2,所以它属于省力杠杆.
(2)由杠杆的平衡条件:F1 L1=F2 L2得:
F1=,
又因为动力臂是阻力臂的3倍
则F1====400N.
故答案为:省力;400.
14、A【考点】杠杆的平衡分析法及其应用.
【分析】从题知,OA处于水平位置,GA对杠杆的拉力为竖直向下,所以G1对杠杆拉力的力臂即为杠杆AO的长度,G2对杠杆拉力的方向也是竖直向下,但OB不是处于水平,所以GB对杠杆拉力的力臂OB′小于OB的长度,根据杠杆的平衡条件分析,即可得出两个物体重力的大小.
【解答】解:根据杠杆的平衡条件:F1L1=F2L2可知,力与相应的力臂成反比关系,
它们的杠杆示意图如右,∵AO=BO,
∴LOA>LOB′,所以物体的重力G1<G2.
故选A.
15、C【考点】杠杆的平衡条件.
【分析】原来杠杆平衡是因为两边的力和力臂的乘积相等.杠杆是否再次平衡要看两边的力和力臂的乘积是否相等.
【解答】解:
设一个钩码的重力为G,横梁上一个格的长度为L,原来杠杆处于平衡状态,则有2G×3L=3G×2L;
A、两边各向外移一格,左边2G×4L=8GL,右边3G×3L=9GL,8GL<9GL,杠杆右端下沉;故A错误;
B、两边各往内移一格,左边2G×2L=4GL,右边3G×1L=3GL,4GL>3GL,杠杆左端下沉;故B错误;
C、左侧的钩码向内移一格,右侧减去一个钩码,左边2G×2L=4GL,右边2G×2L=4GL;4GL=4GL,杠杆平衡;故C正确;
D、在两侧钩码下方,同时加挂一个相同的钩码,左边3G×2L=6GL,右边4G×2L=8GL,6GL<8GL,杠杆右端下沉,故D错误.
故选C.
16、C【考点】杠杆的分类;杠杆及其五要素.
【分析】本题主要考查杠杆的五要素和判断杠杆是否省力的方法.在杠杆中硬棒绕着转动的点叫做支点;动力臂大于阻力臂的杠杆为省力杠杆.
【解答】解:由图可知车厢绕着点C转动,所以C点为支点;
当物体A放在车厢的后部时,动力臂大于阻力臂,因此省力,所以选项A、B、D都不正确.
故选C.
17、C.
18、C.
19、A.
20、C.
21、A.
二、填空题
22、【考点】杠杆的平衡条件.
【分析】(1)当动力臂小于阻力臂时,动力大于阻力,杠杆是费力力杠杆;
(2)根据杠杆平衡的条件F1L1=F2L2可直接求出动力F1的大小;
(3)若仅增加物重,根据杠杆平衡的条件F1L1=F2L2可直接求出;
(4)若拉力方向变为图中虚线所示方向,阻力的力臂不变,拉力的力臂变小,根据杠杆的平衡条件可知拉力的变化.
【解答】解:由图可知,O点为支点,OA为动力臂,OB为阻力臂,阻力大小等于所挂物体的重力,在A点的拉力为动力;
(1)由图可知,OB小于OA,即动力臂小于阻力臂,所以是费力杠杆;钓鱼竿就是此杠杆类型;
(2)已知OB和BA长度之比为3:5,则OB:OA=3:8,由杠杆的平衡条件可知:F OB=G OA,
所以,F==×15N=40N;
(3)若仅增加物重,则F2=G+△G,F1=F+△F;
由杠杆的平衡条件可知:F1 OB=F2 OA,即:(F+△F) OB=(G+△G) OA,
所以,F OB+△F OB=G OA+△G OA,
由于F OB=G OA,所以,△F OB=△G OA,则==;
(4)若拉力方向变为图中虚线所示方向,阻力及阻力臂不变,拉力的力臂变小,由杠杆的平衡条件F1L1=F2L2可知拉力将变大.
故答案为:(1)钓鱼竿;(2)40;(3)8:3;(4)大.
23、【考点】杠杆的动态平衡分析.
【分析】一个铁块和一个体积较小的铁块挂在杠杆的两端,杠杆处于平衡状态,则F1L1=F2L2,两个铁块同时浸没到水中,杠杆受到的动力和阻力都发生改变,杠杆是否还平衡,取决于F′1L1与F′2L2的乘积,若F′1L1=F′2L2,杠杆平衡;若F′1L1≠F′2L2,杠杆就不平衡,将会向较大的方向转动.
【解答】解:两个铁块的质量不相等,杠杆平衡时,根据杠杆的平衡条件:
M1gL1=M2gL2,
又M1>M2,所以L1<L2,即M2离支点较远些;
M1>M2,密度相同,所以V1>V2,设杠杆处于平衡状态;
则F1=G1=ρ铁V1g,F2=G2=ρ铁V2g,
根据杠杆的平衡条件可得:
F1L1=F2L2,即:ρ铁V1gL1=ρ铁V2gL2;
V1L1=V2L2.
将两个同时浸没到水中,两个铁块受到浮力作用,对杠杆的拉力分别为:
F′1=G1﹣F浮1=ρ铁V1g﹣ρ水V1g=(ρ铁﹣ρ水)V1g;
F′2=G2﹣F浮2=ρ铁V2g﹣ρ水V2g=(ρ铁﹣ρ水)V2g;
F′1L1=(ρ铁﹣ρ水)V1gL1;
F′2L2=(ρ铁﹣ρ水)V2gL2;
又V1L1=V2L2;
所以F′1L1=F′2L2,表明杠杆处于平衡状态.
故答案为:M2;能.
24、【分析】要使在B端施加的力最小,就要使动力臂最长,过B做杠杆的垂线,沿此方向用力动力臂最长,动力最小,利用杠杆的平衡条件求用力大小.
【解答】解:如图,过B做杠杆的垂线,沿此方向(竖直向下)用力动力臂最长为OB,最省力,
OB:OA=5:2,
∵杠杆平衡,
∴F×OB=G×OA,
∴.
故答案为:4,竖直向下.
25、900
费力
26、【考点】杠杆的平衡分析法及其应用.
【分析】观察图,从中找出杠杆的几个要素,再根据杠杆的平衡条件可知,要想得到一个最小的力,应使力臂达到最大,可判断力的方向.并结合已知条件计算所施加力的大小.
【解答】解:读图可知,图中AB相当于杠杆,O为支点,FA可视为动力,阻力施到B点,此时为了使用力最小,应使力臂最长,且所施力的方向应阻碍杠杆的转动,故想让转盘反方向转动,乙应沿图中F2方向施力.
此时动力的力臂为L1=50cm=0.5m,阻力的力臂L2=40cm=0.4m,
由杠杆的平衡条件得,FA L1=F2 L2,
则F2===25N.
故答案为:F2;25.
27、【考点】杠杆的平衡条件.
【分析】要解决此题,首先掌握杠杆的平衡条件:F1L1=F2L2.确定支点、力及力臂,代入公式便可求出.同时要掌握重力和质量的计算,掌握G=mg并会对其进行变形.
【解答】解:设每个小格的长度为L,则LA=3L、LB=4L.
根据杠杆的平衡条件:F1L1=F2L2
则F LB=G LA
代入数据得,F×4L=2N×3L
所以F=1.5N
F<G,所以是省力杠杆.
测力计的最大示数为5N,当测力计竖直向上拉并且拉力为5N时,动力臂最长,测出的物体质量最大.
测力计的最大力臂是6L,最大示数为5N,物体拉力的最小力臂为L,
F′ LF′=G′ LG′
代入数据得,5N×6L=G′×L
G′=30N
根据G=mg得,m===3kg
故答案为:1.5;省力;3.
三、实验,探究题
28、【考点】杠杆的应用.
【分析】(1)做出力臂L2的示意图,当α角增大时,由图分析得出力臂L2变化,根据杠杆平衡条件即可判断中F1的变化;
(2)如果考虑到人上半身的重力,根据重力对杠杆的作用,利用杠杆平衡条件即可判断实际拉力的变化;
(3)比较两种状态下力臂L1变化,利用杠杆平衡条件即可判断拉力的不同;根据拉力的大小变化可判断姿势的产生的后果.
【解答】解:(1)如图为杠杆示意图:
由图可知:当α角增大时,力臂L2变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA这段距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小;
(2)如果考虑到人上半身的重力,由于上半身的重力会阻碍杠杆的转动,根据杠杆平衡条件可知:实际拉力将变大;
(3)比较甲、乙两种姿势可知:甲的支点太高,在搬起物体时,阻力臂减小得慢,则腰背部复杂肌肉的等效拉力F1要比较长时间的使用较大的力,所以甲姿势不正确,乙姿势比较正确.
故答案为:(1)变小;变小;(2)大;(3);(4)乙.
29、 (1)左
(2)1.5
(3)变大
30、【考点】探究杠杆的平衡条件实验.
【分析】(1)调节杠杆在水平位置平衡时,平衡螺母向上翘的一端移动;探究杠杆平衡条件时,使杠杆在水平位置平衡,这样方便测量力臂;
(2)设一个钩码重为G,杠杆一个小格是L,根据杠杆平衡条件判断在B点挂钩码的数量;根据杠杆平衡条件判断是否平衡;
(3)根据钩码个数与每个钩码的重力求出测力计拉力;当拉力F向右倾斜时,保持B点不动,弹簧测力计的方向向右倾斜,这时杠杆右侧的力臂变短,根据杠杆的平衡条件可知,使杠杆仍在水平位置平衡,则弹簧测力计的示数将变大;
(4)当弹簧测力计在C点斜向上拉(与水平方向成30°角)动力臂是OC,根据杠杆的平衡条件求出弹簧测力计的读数.
【解答】解:(1)调节杠杆在水平位置平衡,杠杆右端偏高,左端的平衡螺母应向上翘的右端移动,使杠杆在水平位置平衡,力臂在杠杆上,便于测量力臂大小,同时消除杠杆自重对杠杆平衡的影响;
(2)设杠杆每个格的长度为L,每个钩码的重力为G,根据杠杆的平衡条件:FALA=FBLB,即4G×3L=FB×2L,解得FB=6G,需挂6个钩码;
若A、B两点的钩码同时向远离支点的方向移动一个格,则左侧4G×4L=16GL,右侧6G×3L=18GL,因为16GL<18GL
杠杆不能平衡;
(3)保持B点不变,若拉力F向右倾斜时,此时F的力臂变短,根据杠杆的平衡条件,力变大;
(4)当弹簧测力计在C点斜向上拉(与水平方向成30°角)杠杆,此时动力臂等于OC=×4×2cm=4cm;根据杠杆的平衡条件F1L1=F2L2得F1===3N.
故答案为:(1)右;力臂的大小;(2)6;不能;(3)变大(4)4;3.
31、【考点】探究杠杆的平衡条件实验.
【分析】(1)调节杠杆的平衡时,应将平衡螺母向较高一侧调节;
(2)力臂是支点到力的作用线的垂直距离.由此分析为便于测量力臂,弹簧测力计拉力的方向应竖直向下;
(3)根据杠杆平衡条件分析;
(4)弹簧测力计读数时首先认清分度值,然后再读数;弹簧测力计竖直向下拉杠杆时,力臂在杠杆上,当弹簧测力计倾斜拉杠杆时,力臂变短,阻力、阻力臂不变,动力臂变短,动力变大.
【解答】解:(1)调节杠杆的平衡时,由图a杠杆左高右低,应将两端的平衡螺母向左调节;
(2)力臂是支点到力的作用线的垂直距离.当弹簧测力计拉力方向与杠杆垂直时,拉力作用点到支点的距离就是其力臂,这样便于从杠杆上直接读出力臂,由图杠杆水平平衡时拉力方向应竖直向下;
(3)当弹簧测力计的示数达到量程仍不能使杠杆水平平衡,根据杠杆的平衡条件,可以减少左侧钩码的数量或者左侧钩码悬挂点右移.
(4)图中所示的弹簧测力计的分度值是0.2N,故示数为1.8N,弹簧测力计沿虚线方向拉,仍然使杠杆在原来的位置平衡时,动力臂变小,阻力、阻力臂不变,根据杠杆平衡条件得,动力变大,弹簧测力计示数变大;
因为所以动力阻力、阻力臂不变,所以阻力和阻力臂乘积不变,根据杠杆平衡条件可知,动力和动力臂乘积也不变,当弹簧测力计逆时针转动60°,沿图示虚线方向拉时,动力臂变为原来的,则动力为原来的2倍,即F=2×1.8N=3.6N,则弹簧测力计的示数将为3.6N.
故答案为:(1)左;(2)竖直向下;(3)左侧钩码悬挂点右移;(4)1.8;3.6;
【点评】本题考查了学生对杠杆平衡条件的掌握和运用,根据动力臂最长时最省力,力臂变小,力就变大,此类题型要熟练掌握.
12.1
杠杆练习
选择题
1、图中正在使用的机械,属于费力杠杆的有( )
A.①③
B.②③
C.①④
D.②④
2、如图所示,OAB为轻质杠杆,可绕支点O自由转动,在B端施加一个动力使杠杆在水平位置平衡,该杠杆( )
A.一定是省力杠杆
B.一定是费力杠杆
C.一定是等臂杠杆
D.以上情况都有可能
3、如图所示,活塞式抽水机手柄可以看做是绕O点转动的杠杆.它在动力F1和阻力F2的作用下,处于平衡状态,要想最省力应使F1沿着那个方向?( )
A.由C指向F
B.由C指向D
C.由C指向E
D.由C指向O
4、如图所示,是一种指甲刀的结构示意图,下列说法正确的是( )
A.ABC是一个省力杠杆
B.D处刀刃较薄,可以增大压力
C.杠杆ABC上有粗糙的花纹,可以减小摩擦
D.指甲刀只有两个杠杆,一个省力杠杆,一个费力杠杆
5、如图所示,杠杆始终处于水平平衡状态,改变弹簧测力计拉力的方向,使其从①②③,此过程中,弹簧测力计的示数将(
)
A.
逐渐变大
B.
逐渐变小
C.
先变大后变小
D.
先变小后变大
6、如图所示的工具中,正常使用时属于费力杠杆的是
(
)
7、如图所示是小明同学研究杠杆平衡条件的实验装置和操作图,关于此实验下列说法正确的是( )
A.若实验前杠杆如图甲所示,则需要将杠杆的平衡螺母向左调节
B.小明的其中一步实验如图乙所示,则需要在D点挂3个相同的钩码,就可以让杠杆恢复平衡
C.若在A点用弹簧测力计拉杠杆使杠杆平衡,则此时杠杆可能是费力杠杆
D.为了保持杠杆在水平位置平衡,在D点施加力的方向由①位置到②位置的过程中,所需施加的拉力大小不变
8、汶川大地震中,巨大的石头挡住了救援车辆的通路,救援人员用撬棍将石头撬开.如果在撬棍a端分别沿如图所示三个方向用力,其中最省力的是( )
A.沿F1方向
B.沿F2方向
C.沿F3方向
D.三个方向所用力一样大
9、如图甲所示,小华用笤帚在扫地,O为支点,作用在A点的动力为F1,笤帚质量忽略不计,在笤帚的B点受力为F2,F2的方向沿bb′线(图乙),若笤帚在图所示位置处于平衡状态.则( )
A.F2>F1
B.F2方向沿bb′线向右
C.F1力臂等于s1
D.F2力臂等于s2
10、如图所示,可绕O点转动的轻质杠杆,在D点挂一个重为G的物体M,用一把弹簧测力计依次在A,B,C三点沿圆O相切的方向用力拉,都使杠杆在水平位置平衡,读出三次的示数分别为F1、F2、F3,它们的大小关系是( )
A.F1<F2<F3<G
B.F1>F2>F3>G
C.F1=F2=F3=G
D.F1>F2=F3=G
11、有一种多功能剪刀,如图所示,图中标注了该剪刀的相关用途.对于它的使用,以下分析正确的是( )
A.做为剪刀使用时:物体越靠近O点越省力
B.做为启瓶器使用时:它是一个费力杠杆
C.做为削皮刀使用时:刀刃很锋利,是为了增大压力把果皮削掉
D.做为挤压钳使用时:挤压齿尖锐,是为了减小压强把果壳挤开
12、如图所示为等刻度轻质杠杆,A处挂2牛的物体,若使杠杆在水平位置平衡,则在B处施加的力( )
A.可能为0.5牛
B.一定为1牛
C.可能为2牛
D.一定是4牛
13、如图是人抬独轮车车把时的简化示意图,此时独轮车相当一个______杠杆;若动力臂是阻力臂的3倍,物体和车总重G为1200N,则抬起车把的力F为______N.
14、如图所示,杠杆AOB用细线悬挂起来,当A端挂重物G1,B端挂重物G2时,杠杆平衡,此时OA恰好处于水平位置,AO=BO,杠杆重力不计,则( )
A.G1<G2
B.G1>G2
C.G1=G2
D.都有可能
15、如图所示,杠杆的水平位置平衡,下列操作仍能让杠杆在水平位置保持平衡的是( )
A.两侧钩码同时向外移一格
B.两侧钩码同时向内移一格
C.左侧的钩码向内移一格,右侧减去一个钩码
D.在两侧钩码下方,同时加挂一个相同的钩码
16、如图所示,是自卸车的示意图,车厢部分可视为杠杆,则下列分析正确的是( )
A.B点是支点,液压杆施的力是动力,货物重力是阻力
B.B点是支点,物体A放在车厢前部可省力
C.C点是支点,物体A放在车厢后部可省力
D.C点是支点,物体A放在车厢前部可省力
17、在质量可忽略的杠杆的A、B两端各挂有体积相同的铜块和铝块(ρ铜>ρ铝),支点O在如图所示的位置时,杠杆在水平位置保持平衡.在下列情况下,杠杆仍然在水平位置保持平衡的是( )
A.在铜块和铝块上各加一块质量相等的物体
B.将铜块和铝块同时向支点移动一小段相同的距离
C.将铜块和铝块各切去体积相同的一小部分
D.将铜块和铝块同时浸没在水中
18、如图所示,杠杆上分别放着质量不相等的两个球,杠杆在水平位置平衡,如果两球以相同速度同时匀速向支点移动,则杠杆( )
A.仍能平衡
B.不能平衡,大球那端下沉
C.不能平衡,小球那端下沉
D.无法判断
19、一根轻质杠杆,在左右两端分别挂在300牛的铜块和200牛的铝块时,杠杆恰好平衡.若将两边物重同时减少50牛,则杠杆( )
A.左端下沉
B.右端下沉
C.仍然平衡
D.无法确定
20、前不久,台风“卡努”经过常州,吹倒了一些树木,园林工人在扶正被风吹倒的树木后,还用绳索牵拉固定(绳的一端绑在木桩上),如图所示,则下列措施最合适的是( )
A.绳的另一端系在A点
B.绳的另一端系在B点
C.在A点垫上木板,再系上绳
D.在B点垫上木板,再系上绳
21、如如图所示杠杆,O是支点,中间挂一重物G,如果在杠杆的另一端M处加一个力F使杠杆平衡,且要求所加的力要最小,则这个力( )
A.应沿MQ方向
B.应沿MP方向
C.应沿MN方向
D.可沿任意方向
二、填空题
22、如图,轻杆OA可绕O点自由转动,用细线将15N的重物挂在A处,小林在B处用竖直向上的拉力提住轻杆,OB和BA长度之比为3:5,下列问题中,轻杆始终在水平位置处于平衡.
(1)此杠杆类型与 相同(选填“钓鱼竿”或“羊角锤”);
(2)拉力大小为 N;
(3)若仅增加物重,则拉力的变化量与物重的变化量之比为 ;
(4)若拉力方向变为图中虚线所示方向,则拉力将变 .
23、在一轻质杠杆的两端分别挂上质量不等的两个铁块M1、M2(M1>M2),调节两物体到支点的距离,使杠杆平衡,则 (选填“M1”或“M2”)离支点较远些.然后将物体同时浸没在水中,杠杆 (选填“能”或“不能”)保持平衡.
24、如图所示,重为10N的物体G挂在杠杆的A端(杠杆重力不计),要使杠杆在图示位置平衡,在B端至少要施加 N的力,力的方向是 .
25、轻质木棒
AB
可以绕
O
点转动,OA
:
OB
=
3
:
1,A
端细线下挂
300N
的重物静止在水平地面上,若使木杆保持水平位置,且重物对水平地面的压力为零,在
B
点要用_____N的力竖直向下拉,此时木棒为_____(省力/费力/等臂)杠杆。
26、如图为水平桌面上的圆形玻璃转盘(转盘半径为50cm),在水平力作用下能绕转盘中心O点自由转动,转动时可视为杠杆.甲在A点施加一个大小为20N的水平力FA,想让转盘转动,对面的乙在距O点40cm处的B点同时施加一个水平力,想让转盘反方向转动,乙应沿图中 (选填“F1”、“F2”、“F3”或“F4”)方向施加一个至少为 N的力,才可能达到目的(假设只有甲、乙两人对转盘施力,忽略其它力对转动的影响).
27、如图所示,在已经处于水平位置平衡的杠杆的A点悬挂两个总重为2N的钩码,在B点用弹簧测力计竖直向上拉,使杠杆在水平位置再次平衡,则拉力应为 N,此时的杠杆属于 (选填“省力”或“费力”)杠杆.如果测力计的量程为0~5N,在支点不变的情况下,采用图中的杠杆,能较为精确地测量出悬挂物体的最大质量为 kg.(g取10N/kg)
三、实验,探究题
28、从地面上搬起重物我们的常见做法是弯腰(如图甲)或人下蹲弯曲膝盖(如图乙)把它搬起来,哪种方法好呢?下面就建立模型说明这个问题.把脊柱简化为杠杆如图丙所示,脊柱可绕骶骨(轴)O转动,腰背部复杂肌肉的等效拉力F1作用在A点,其实际作用方向与脊柱夹角为12°且保持不变,搬箱子拉力F2作用在肩关节B点,在B点挂一重物代替箱子.用测力计沿F1方向拉,使模型静止,可测出腰背部复杂肌肉拉力的大小.接着,改变脊柱与水平面的夹角即可改变杠杆与水平面的夹角α,多次实验得出结论.
(1)当α角增大时,F2的力臂L2 (变大/不变/变小),F1 (变大/不变/变小).
(2)如果考虑到人上半身的重力,那么腰背部肌肉的实际拉力将比丙图中F1要 (大/小).
(3)对比甲乙两种姿势所对应丙图中的两种状态,由以下分析可得, (甲/乙)图中的姿势比较正确.
29、如图所示,是探究杠杆平衡条件的实验装置,已知杠杆上刻度均匀,每个钩码质量均为50g。
(1)将杠杆中点置于支架上,不挂钩码,当杠杆静止时,发现杠杆左端上翘.此时应将杠杆两端的平衡螺母向_______(选填“左”或“右”)调节,使杠杆在水平位置平衡;
(2)当凋节杠杆在水平平衡后,在A点悬挂两个钩码,要使杠杆在水平位置再次平衡,需在B点悬挂总重为_______N的钩码;
(3)撤去B点所挂钩码,改用弹簧测力计在C点竖直向上拉,使杠杆在水平位置平衡。若此时改变弹簧测力计拉力的方向,使之斜向左上方拉,杠杆仍然在水平位置平衡,则测力计的读数将_______
(选填“变大”、“不变”或“变小”)。
30、在“探究杠杆平衡条件的实验”中:
(1)如图甲所示,实验前,杠杆左端下沉,则应将左端的平衡螺母向 调节(选填“左”或“右”,直到杠杆在水平位置平衡,目的是便于测量 .
(2)如图乙所示,杠杆上的刻度均匀,在A点挂4个钩码,要使杠杆在水平位置平衡,应在B点挂 个相同的钩码;当杠杆平衡后,将A、B两点下方所挂的钩码同时朝远离支点O方向移动一小格,则杠杆 (选填“能”或”不能“)在水平位置保持平衡.
(3)如图丙所示,若不在B点挂钩码,改用弹簧测力计在B点向下拉杠杆,使杠杆仍在水平位置平衡,当测力计从a位置转动b位置时,其示数大小将 .
(4)如图丁所示,已知每个钩码重0.5N,杠杆上每小格长度为2cm,当弹簧测力计在C点斜向上拉(与水平方向成30°角)杠杆,使杠杆在水平位置平衡时,拉力F的力臂大小为 cm,弹簧测力计示数的大小为 N.
31、在探究杠杆平衡条件的实验中.
(1)如图a所示,要使杠杆在水平位置平衡,可将杠杆左端的平衡螺母向 调节.
(2)如图b所示,调节平衡后,左侧挂上钩码,在右侧用弹簧测力计(图中未画出)拉杠杆,使其在水平位置平衡,为便于测量力臂,应使弹簧测力计拉力的方向 .
(3)操作过程中,当弹簧测力计的示数达到量程仍不能使杠杆水平平衡,在不更换弹簧测力计的情况下,你认为接下来合理的操作是 .(写出一条即可)
(4)如图c所示,在A点挂上钩码,在B点用弹簧测力计竖直向上拉,使杠杆处于水平位置平衡,则此时弹簧测力计的示数是 N;将弹簧测力计逆时针转动60°,沿图示虚线方向拉,仍使杠杆在水平位置平衡,则弹簧测力计的示数将为 N.
参考答案
一、选择题
1、A【考点】杠杆的分类.
【分析】本题的解题关键是通过生活经验,体会支点的位置,判断出动力臂与阻力臂的长度关系,进而得出省力、费力情况.
【解答】解:①钓鱼竿在使用过程中,动力臂小于阻力臂,是费力杠杆;
②羊角锤在使用过程中,动力臂大于阻力臂,是省力杠杆;
③筷子在使用过程中,动力臂小于阻力臂,是费力杠杆;
④核桃夹在使用过程中,动力臂大于阻力臂,是省力杠杆.
综上所述,属于费力杠杆的有①③.
故选A.
2、D【考点】杠杆的分类.
【分析】使用杠杆时,如果动力臂大于阻力臂,为省力杠杆;如果动力臂等于阻力臂,为等臂杠杆;如果动力臂小于阻力臂,为费力杠杆;
因为在B点用力的方向不确定,所以其省费力情况要根据用力的方向确定.据此分析.
【解答】解:B点力的方向不同,力臂的大小则不同,不能确定动力臂与阻力臂的大小关系,所以此时杠杆可能省力,可能费力,可能既不省力也不费力.故ABC不符合题意,D符合题意.
故选D.
3、A【考点】杠杆中最小力的问题.
【分析】活塞式抽水机手柄可以看作是绕O点转动的杠杆,选项中的四个量应该分别代表了杠杆的动力、动力臂、阻力、阻力臂,关键是看它们的对应关系是否正确,据此来做出判断.
【解答】解:读图可知,F1为动力,其力臂是支点到动力作用线的垂直距离,此时力臂为OE;F2为阻力,其力臂是从支点到阻力作用线的垂直距离;
处于平衡状态,根据杠杆的平衡条件,要想最省力,力臂最长,应为OF,即F1沿着由C指向F方向,只有选项A符合题意.
故选A.
4、A【考点】杠杆的分类;摩擦力大小的影响因素;压强.
【分析】(1)对于杠杆类型的判断可从动力臂与阻力臂的大小关系上入手;
(2)压强的大小与压力的大小和受力面积的大小有关;
(3)滑动摩擦力的大小与压力的大小和接触面的粗糙程度有关.
【解答】解:A、对于ABC,如图所示,在使用时,它的动力臂大于阻力臂,所以它是省力杠杆,符合题意;
B、在相同的压力下,D处刀刃较薄,受力面积小,产生的压强大,压力的作用效果明显,并不是压力增大了,不符合题意;
C、杠杆ABC上有粗糙的花纹,增大接触面的粗糙程度,可以增大摩擦,不符合题意;
D、指甲刀中有三个杠杆:ABC、OBD、0ED,其中ABC是省力杠杆,其它两个都是费力杠杆,不符合题意.
故选A.
5、D
6、A
7、C【考点】杠杆的平衡条件.
【分析】(1)根据杠杆的平衡条件可知,杠杆倾斜时,杠杆的重心偏向杠杆下沉的一端,左、右两端的螺母(或一端的螺母)要向杠杆上翘的一端调节;
(2)根据杠杆的平衡条件分析解答;
(3)分析动力臂与阻力臂的大小,来确定是否为省力杠杆;
(4)由杠杆的平衡条件,在阻力阻力臂不变时,动力臂减小,动力变大.
【解答】解:
A、如图甲可知,杠杆左端下沉,则需要将平衡螺母向右调节,故A错误;
B、左侧力与力臂的乘积3G×4L=12GL;在D点挂3个相同钩码,右侧力与力臂的乘积3G×3L=9GL,左右两侧力与力臂的乘积不相等,故杠杆不平衡,B错误;
C、若在A点用弹簧测力计拉杠杆使杠杆平衡,由于没有明确力的方向,动力臂可能小于阻力臂,则此时杠杆可能是费力杠杆,故C正确;
D、为了保持杠杆在水平位置平衡,在D点施加力的方向由①位置到②位置的过程中,阻力和阻力臂不变,动力臂减小,由杠杆平衡条件可知,动力变大,故D错误.
故选C.
8、B
9、B
10、C【考点】杠杆的平衡条件.
【分析】利用杠杆平衡条件分析,当阻力和阻力臂不变时,如果动力臂不变,只改动用力方向,其动力不变,据此分析解答.
【解答】解:设拉力的力臂为L,则由题意可知,当杠杆在水平位置平衡时:G×OD=F×L
由此可得:F=
因为G,OD不变,OD=L=r,故F=G,由于F1、F2、F3的力臂都为圆的半径,相等,故F1=F2=F3=G
故选:C
11、A【考点】杠杆的应用;增大压强的方法及其应用.
【分析】多功能剪刀的不同部位有不同的用途,那是因为它的不同部位可以构成不同的简单机械或者是利用了不同的物理学原理.
【解答】解:A、做剪刀使用时:当所剪物体放在边缘时,动力臂小于阻力臂,是费力杠杆;当所剪物体放在靠里边时,动力臂大于阻力臂,是省力杠杆;当放在与动力臂相同的地方,是等臂杠杆,即不省力也不费力;所以物体越靠近O点越省力,故A正确;
B、做为启瓶器使用时,应用了杠杆的知识,动力臂大于阻力臂,是一个省力杠杆,故B错误.
C、做削皮刀使用时:刀刃很锋利,是在压力一定的条件下,减小接触面积增大压强,故C错误;
D、做挤压钳:应用了压强和摩擦力的知识.挤压齿尖且参差不齐,不仅通过减小受力面积的方法增大了压强;还通过增加表面粗糙程度的方法增大了摩擦力,既利于挤压果壳.又避免坚果滑落,故D错误;
12、C【考点】杠杆的平衡条件;杠杆中最小力的问题.
【分析】根据杠杆平衡的条件和杠杆中最小力的问题进行分析,即动力乘以动力臂等于阻力乘以阻力臂,支点与力的作用点的连线为最长力臂.
【解答】解:根据杠杆平衡的条件求出在B处施加最小的力为:
F1L1=F2L2
由题意可知,只有杠杆自重等不计,力的方向与杠杆垂直时,力的大小才是1N,但如果力的方向与杠杆不垂直,则力将会大于1N,即有可能是2N.
故选C.
13、【考点】杠杆的平衡分析法及其应用.
【分析】(1)根据动力臂与阻力臂的大小关系判断杠杆的类型.
(2)根据杠杆的平衡条件计算动力的大小.
【解答】解:(1)如图,抬独轮车车把时,动力臂L1大于阻力臂L2,所以它属于省力杠杆.
(2)由杠杆的平衡条件:F1 L1=F2 L2得:
F1=,
又因为动力臂是阻力臂的3倍
则F1====400N.
故答案为:省力;400.
14、A【考点】杠杆的平衡分析法及其应用.
【分析】从题知,OA处于水平位置,GA对杠杆的拉力为竖直向下,所以G1对杠杆拉力的力臂即为杠杆AO的长度,G2对杠杆拉力的方向也是竖直向下,但OB不是处于水平,所以GB对杠杆拉力的力臂OB′小于OB的长度,根据杠杆的平衡条件分析,即可得出两个物体重力的大小.
【解答】解:根据杠杆的平衡条件:F1L1=F2L2可知,力与相应的力臂成反比关系,
它们的杠杆示意图如右,∵AO=BO,
∴LOA>LOB′,所以物体的重力G1<G2.
故选A.
15、C【考点】杠杆的平衡条件.
【分析】原来杠杆平衡是因为两边的力和力臂的乘积相等.杠杆是否再次平衡要看两边的力和力臂的乘积是否相等.
【解答】解:
设一个钩码的重力为G,横梁上一个格的长度为L,原来杠杆处于平衡状态,则有2G×3L=3G×2L;
A、两边各向外移一格,左边2G×4L=8GL,右边3G×3L=9GL,8GL<9GL,杠杆右端下沉;故A错误;
B、两边各往内移一格,左边2G×2L=4GL,右边3G×1L=3GL,4GL>3GL,杠杆左端下沉;故B错误;
C、左侧的钩码向内移一格,右侧减去一个钩码,左边2G×2L=4GL,右边2G×2L=4GL;4GL=4GL,杠杆平衡;故C正确;
D、在两侧钩码下方,同时加挂一个相同的钩码,左边3G×2L=6GL,右边4G×2L=8GL,6GL<8GL,杠杆右端下沉,故D错误.
故选C.
16、C【考点】杠杆的分类;杠杆及其五要素.
【分析】本题主要考查杠杆的五要素和判断杠杆是否省力的方法.在杠杆中硬棒绕着转动的点叫做支点;动力臂大于阻力臂的杠杆为省力杠杆.
【解答】解:由图可知车厢绕着点C转动,所以C点为支点;
当物体A放在车厢的后部时,动力臂大于阻力臂,因此省力,所以选项A、B、D都不正确.
故选C.
17、C.
18、C.
19、A.
20、C.
21、A.
二、填空题
22、【考点】杠杆的平衡条件.
【分析】(1)当动力臂小于阻力臂时,动力大于阻力,杠杆是费力力杠杆;
(2)根据杠杆平衡的条件F1L1=F2L2可直接求出动力F1的大小;
(3)若仅增加物重,根据杠杆平衡的条件F1L1=F2L2可直接求出;
(4)若拉力方向变为图中虚线所示方向,阻力的力臂不变,拉力的力臂变小,根据杠杆的平衡条件可知拉力的变化.
【解答】解:由图可知,O点为支点,OA为动力臂,OB为阻力臂,阻力大小等于所挂物体的重力,在A点的拉力为动力;
(1)由图可知,OB小于OA,即动力臂小于阻力臂,所以是费力杠杆;钓鱼竿就是此杠杆类型;
(2)已知OB和BA长度之比为3:5,则OB:OA=3:8,由杠杆的平衡条件可知:F OB=G OA,
所以,F==×15N=40N;
(3)若仅增加物重,则F2=G+△G,F1=F+△F;
由杠杆的平衡条件可知:F1 OB=F2 OA,即:(F+△F) OB=(G+△G) OA,
所以,F OB+△F OB=G OA+△G OA,
由于F OB=G OA,所以,△F OB=△G OA,则==;
(4)若拉力方向变为图中虚线所示方向,阻力及阻力臂不变,拉力的力臂变小,由杠杆的平衡条件F1L1=F2L2可知拉力将变大.
故答案为:(1)钓鱼竿;(2)40;(3)8:3;(4)大.
23、【考点】杠杆的动态平衡分析.
【分析】一个铁块和一个体积较小的铁块挂在杠杆的两端,杠杆处于平衡状态,则F1L1=F2L2,两个铁块同时浸没到水中,杠杆受到的动力和阻力都发生改变,杠杆是否还平衡,取决于F′1L1与F′2L2的乘积,若F′1L1=F′2L2,杠杆平衡;若F′1L1≠F′2L2,杠杆就不平衡,将会向较大的方向转动.
【解答】解:两个铁块的质量不相等,杠杆平衡时,根据杠杆的平衡条件:
M1gL1=M2gL2,
又M1>M2,所以L1<L2,即M2离支点较远些;
M1>M2,密度相同,所以V1>V2,设杠杆处于平衡状态;
则F1=G1=ρ铁V1g,F2=G2=ρ铁V2g,
根据杠杆的平衡条件可得:
F1L1=F2L2,即:ρ铁V1gL1=ρ铁V2gL2;
V1L1=V2L2.
将两个同时浸没到水中,两个铁块受到浮力作用,对杠杆的拉力分别为:
F′1=G1﹣F浮1=ρ铁V1g﹣ρ水V1g=(ρ铁﹣ρ水)V1g;
F′2=G2﹣F浮2=ρ铁V2g﹣ρ水V2g=(ρ铁﹣ρ水)V2g;
F′1L1=(ρ铁﹣ρ水)V1gL1;
F′2L2=(ρ铁﹣ρ水)V2gL2;
又V1L1=V2L2;
所以F′1L1=F′2L2,表明杠杆处于平衡状态.
故答案为:M2;能.
24、【分析】要使在B端施加的力最小,就要使动力臂最长,过B做杠杆的垂线,沿此方向用力动力臂最长,动力最小,利用杠杆的平衡条件求用力大小.
【解答】解:如图,过B做杠杆的垂线,沿此方向(竖直向下)用力动力臂最长为OB,最省力,
OB:OA=5:2,
∵杠杆平衡,
∴F×OB=G×OA,
∴.
故答案为:4,竖直向下.
25、900
费力
26、【考点】杠杆的平衡分析法及其应用.
【分析】观察图,从中找出杠杆的几个要素,再根据杠杆的平衡条件可知,要想得到一个最小的力,应使力臂达到最大,可判断力的方向.并结合已知条件计算所施加力的大小.
【解答】解:读图可知,图中AB相当于杠杆,O为支点,FA可视为动力,阻力施到B点,此时为了使用力最小,应使力臂最长,且所施力的方向应阻碍杠杆的转动,故想让转盘反方向转动,乙应沿图中F2方向施力.
此时动力的力臂为L1=50cm=0.5m,阻力的力臂L2=40cm=0.4m,
由杠杆的平衡条件得,FA L1=F2 L2,
则F2===25N.
故答案为:F2;25.
27、【考点】杠杆的平衡条件.
【分析】要解决此题,首先掌握杠杆的平衡条件:F1L1=F2L2.确定支点、力及力臂,代入公式便可求出.同时要掌握重力和质量的计算,掌握G=mg并会对其进行变形.
【解答】解:设每个小格的长度为L,则LA=3L、LB=4L.
根据杠杆的平衡条件:F1L1=F2L2
则F LB=G LA
代入数据得,F×4L=2N×3L
所以F=1.5N
F<G,所以是省力杠杆.
测力计的最大示数为5N,当测力计竖直向上拉并且拉力为5N时,动力臂最长,测出的物体质量最大.
测力计的最大力臂是6L,最大示数为5N,物体拉力的最小力臂为L,
F′ LF′=G′ LG′
代入数据得,5N×6L=G′×L
G′=30N
根据G=mg得,m===3kg
故答案为:1.5;省力;3.
三、实验,探究题
28、【考点】杠杆的应用.
【分析】(1)做出力臂L2的示意图,当α角增大时,由图分析得出力臂L2变化,根据杠杆平衡条件即可判断中F1的变化;
(2)如果考虑到人上半身的重力,根据重力对杠杆的作用,利用杠杆平衡条件即可判断实际拉力的变化;
(3)比较两种状态下力臂L1变化,利用杠杆平衡条件即可判断拉力的不同;根据拉力的大小变化可判断姿势的产生的后果.
【解答】解:(1)如图为杠杆示意图:
由图可知:当α角增大时,力臂L2变小;由于拉力F1的方向与脊柱夹角始终为12°,且OA这段距离不变,则O点到F1作用线的距离不变,即动力臂不变,阻力为箱子的重力不变,根据杠杆平衡条件可知,F1变小;
(2)如果考虑到人上半身的重力,由于上半身的重力会阻碍杠杆的转动,根据杠杆平衡条件可知:实际拉力将变大;
(3)比较甲、乙两种姿势可知:甲的支点太高,在搬起物体时,阻力臂减小得慢,则腰背部复杂肌肉的等效拉力F1要比较长时间的使用较大的力,所以甲姿势不正确,乙姿势比较正确.
故答案为:(1)变小;变小;(2)大;(3);(4)乙.
29、 (1)左
(2)1.5
(3)变大
30、【考点】探究杠杆的平衡条件实验.
【分析】(1)调节杠杆在水平位置平衡时,平衡螺母向上翘的一端移动;探究杠杆平衡条件时,使杠杆在水平位置平衡,这样方便测量力臂;
(2)设一个钩码重为G,杠杆一个小格是L,根据杠杆平衡条件判断在B点挂钩码的数量;根据杠杆平衡条件判断是否平衡;
(3)根据钩码个数与每个钩码的重力求出测力计拉力;当拉力F向右倾斜时,保持B点不动,弹簧测力计的方向向右倾斜,这时杠杆右侧的力臂变短,根据杠杆的平衡条件可知,使杠杆仍在水平位置平衡,则弹簧测力计的示数将变大;
(4)当弹簧测力计在C点斜向上拉(与水平方向成30°角)动力臂是OC,根据杠杆的平衡条件求出弹簧测力计的读数.
【解答】解:(1)调节杠杆在水平位置平衡,杠杆右端偏高,左端的平衡螺母应向上翘的右端移动,使杠杆在水平位置平衡,力臂在杠杆上,便于测量力臂大小,同时消除杠杆自重对杠杆平衡的影响;
(2)设杠杆每个格的长度为L,每个钩码的重力为G,根据杠杆的平衡条件:FALA=FBLB,即4G×3L=FB×2L,解得FB=6G,需挂6个钩码;
若A、B两点的钩码同时向远离支点的方向移动一个格,则左侧4G×4L=16GL,右侧6G×3L=18GL,因为16GL<18GL
杠杆不能平衡;
(3)保持B点不变,若拉力F向右倾斜时,此时F的力臂变短,根据杠杆的平衡条件,力变大;
(4)当弹簧测力计在C点斜向上拉(与水平方向成30°角)杠杆,此时动力臂等于OC=×4×2cm=4cm;根据杠杆的平衡条件F1L1=F2L2得F1===3N.
故答案为:(1)右;力臂的大小;(2)6;不能;(3)变大(4)4;3.
31、【考点】探究杠杆的平衡条件实验.
【分析】(1)调节杠杆的平衡时,应将平衡螺母向较高一侧调节;
(2)力臂是支点到力的作用线的垂直距离.由此分析为便于测量力臂,弹簧测力计拉力的方向应竖直向下;
(3)根据杠杆平衡条件分析;
(4)弹簧测力计读数时首先认清分度值,然后再读数;弹簧测力计竖直向下拉杠杆时,力臂在杠杆上,当弹簧测力计倾斜拉杠杆时,力臂变短,阻力、阻力臂不变,动力臂变短,动力变大.
【解答】解:(1)调节杠杆的平衡时,由图a杠杆左高右低,应将两端的平衡螺母向左调节;
(2)力臂是支点到力的作用线的垂直距离.当弹簧测力计拉力方向与杠杆垂直时,拉力作用点到支点的距离就是其力臂,这样便于从杠杆上直接读出力臂,由图杠杆水平平衡时拉力方向应竖直向下;
(3)当弹簧测力计的示数达到量程仍不能使杠杆水平平衡,根据杠杆的平衡条件,可以减少左侧钩码的数量或者左侧钩码悬挂点右移.
(4)图中所示的弹簧测力计的分度值是0.2N,故示数为1.8N,弹簧测力计沿虚线方向拉,仍然使杠杆在原来的位置平衡时,动力臂变小,阻力、阻力臂不变,根据杠杆平衡条件得,动力变大,弹簧测力计示数变大;
因为所以动力阻力、阻力臂不变,所以阻力和阻力臂乘积不变,根据杠杆平衡条件可知,动力和动力臂乘积也不变,当弹簧测力计逆时针转动60°,沿图示虚线方向拉时,动力臂变为原来的,则动力为原来的2倍,即F=2×1.8N=3.6N,则弹簧测力计的示数将为3.6N.
故答案为:(1)左;(2)竖直向下;(3)左侧钩码悬挂点右移;(4)1.8;3.6;
【点评】本题考查了学生对杠杆平衡条件的掌握和运用,根据动力臂最长时最省力,力臂变小,力就变大,此类题型要熟练掌握.
