数学六年级下浙教版5.27比和比例 课件
文档属性
| 名称 | 数学六年级下浙教版5.27比和比例 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 299.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-06 00:00:00 | ||
图片预览










文档简介
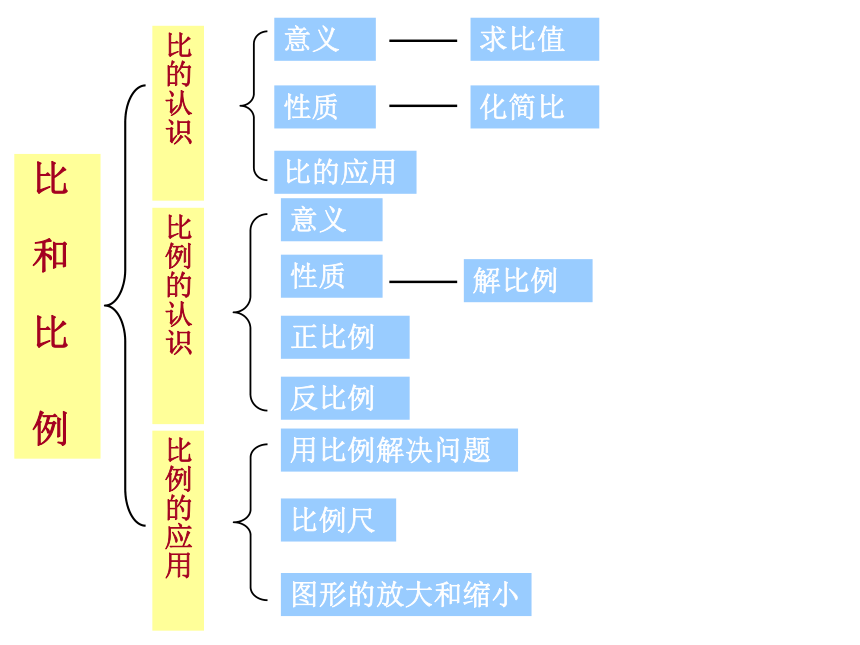
课件65张PPT。 小学数学总复习就是注重帮助学生把分散在各年级、各章节中有关的数学知识上下串联,左右沟通起来。其过程就是把学生的内容、知识,不断重组,并形成良好的认知结构的过程。 比 和 比 例比的认识比例的认识比例的应用意义性质求比值化简比意义性质正比例反比例解比例用比例解决问题比例尺图形的放大和缩小比的应用第一部分:复习内容要点第二部分:复习目标第三部分:复习重、难点第四部分:复习内容分析第五部分:复习课时安排第六部分:复习设想及措施一、复习内容要点●比和比例的意义 ●基本性质 ●解比例 ●按比例分配问题 ●比例尺 ●正比例和反比例的概念 ●用比和比例知识解答的应用题 二、教学目标 ●分清比和比例、正比例和反比例概念间的联系和区别。 ●掌握用比和比例的知识解答应用题的方法。 ●理清应用题与比和比例知识之间的联系。 ●培养学生综合运用数学知识和灵活解题的能力。 三、教学重点、难点 重点:用比和比例知识解答应用题。
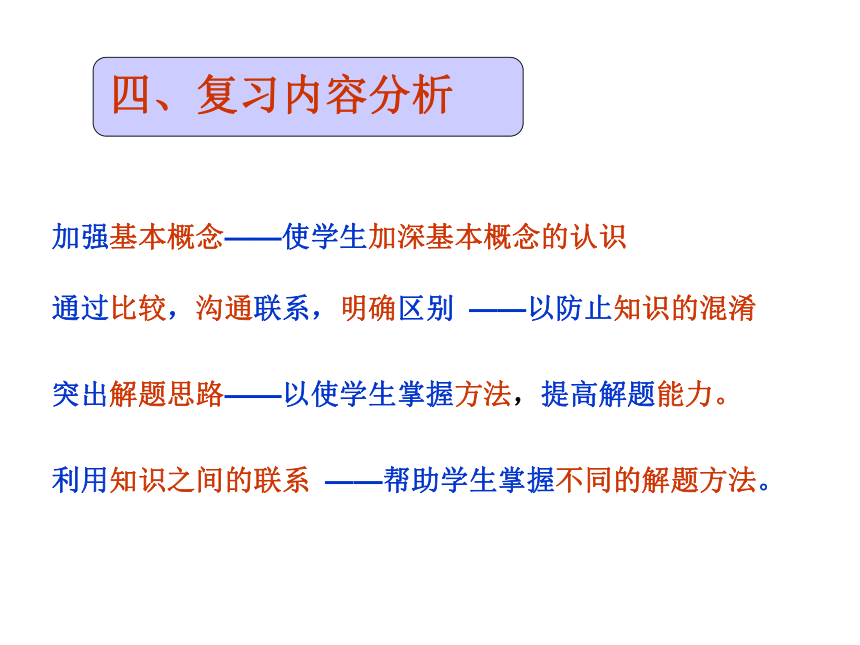
难点:用不同方法灵活解答应用题。四、复习内容分析加强基本概念——使学生加深基本概念的认识 通过比较,沟通联系,明确区别 ——以防止知识的混淆 突出解题思路——以使学生掌握方法,提高解题能力。 利用知识之间的联系 ——帮助学生掌握不同的解题方法。 四、复习内容分析 1、比的概念●比的意义两个数相除又叫做两个数的比。●比值的概念比的前项除以后项所得的商,叫做比值。 例如: 5÷6 可记作 5∶6。 例如:5÷6 = →就是5:6的比值。——是借助于除法的概念建立的。比——表示两个数量之间的关系而且是相除关系。生活中比赛得分2 :1是不是比? 它不是比,它没有一种相除关系在里面,所以它可以用0 :0来表示,而比是不能用0作为后项。 例:一个平行四边形花坛,底是6米,高是4米,6÷4表示( ),这一关系还可以用( )来表示。6 :4四、复习内容分析引导学生思考并归纳比与除法和分数的关系 a :b = a÷b = (b≠0)比的前项相当于分数的分子和除式中的被除数;
比的后项相当于分数的分母和除式中的除数;
比值相当于分数的分数值和除式中的商 比、除法和分数的关系一种
关系被除数分子除号分数线除数分母商分
数
值一种
运算一个数
比值的意义:同类数量的比值:不同类数量的比值:能加单位不能加单位 例:两辆汽车在公路上行驶,甲车行了75千米,耗油10升,乙车行了60千米,耗油9升。75千米:10升=7.5千米/升表示甲车每升汽油能行7.5千米。60千米:75千米= ,表示乙车行的路程是甲车的 。——产生新的量。表示倍数关系或几分之几。四、复习内容分析2、比基本性质: 比的前项和后项同时乘上或者除以相同的数(0除外),比值不变,这叫做比的基本性质。作用: 1、化简比——能让复杂的比依据比的基本性质化简成简单整数比。如0.314:1.256=1:2,也为后面图形的放大和缩小做铺垫。2、求比值——有时候比除法计算简单。四、复习内容分析求比值和化简比 学生容易混淆发生错误 列表对比 引导弄清求比值和化简比的区别 根据比的意义,用前项除以后项。 是一个数,可以是整数、小数或分数。 根据比的基本性质,把比的前项和后项同时乘或除以相同的数(0除外)。 是一个比,它的前项和后项是互质数(两个互质的整数比)。四、复习内容分析 应用比的知识 计算按比例分配问题 引导学生思考按比例分配应用题的解题依据、解题思路和方法。 3、按比例分配问题:四、复习内容分析 在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配的方法通常叫做按比例分配。
●特点:
已知总量和部分量的比,求各部分量是多少。
●解题方法:
先求总份数,再求个部分量占总量的几分之几,最后用总量乘以这个几分之几,求出个部分量。 例:周长32厘米,长和宽的比是5:3,面积多少平方厘米?
2:33:7例:将这两种浓缩液混在一起制成新的清洁液,那么这种新的清洁液中浓缩液是清洁液的百分之几?
(百分号前保留一位小数)250ml 500ml
2:33:7250ml 500ml浓缩液是清洁液的百分之几?250 x + 500 x =150(ml)150÷750×100% ≈33.3%250+500=750(ml)(百分号前保留一位小数) 例:3克的蚂蚁能搬动45克的物体;3吨的大象能拉动4.5吨的物体,蚂蚁和大象谁的力气大?(要求:用学过的知识说明你的观点,回答要全面) 从物体的重量与动物本身的重量的比或比值看是蚂蚁的力气大,但是如果从动物驮的物体的重量来看是大象的力气大。3:45 =1:15 或 45:3=15
3:4.5 =1:1.5 4.5:3=1.5黄金比我的上半身的高度是65cm,下半身高度是98cm。当一个人上半身的高度与下半身的比是0.618:1时,这个人身材看上去就很美。四、复习内容分析 4、比例的意义表示两个比相等的式子叫做比例。 与图形的放大和缩小联系比较紧密,图形放大和缩小的结果,就组成了比例。能组成比例的两个图形,形状相同,大小不同。 例:将上题中的平行四边形按照一定比例缩小,画在平面图上,量得图上平行四边形的底是3厘米,高是2厘米。那么图上平行四边形的底与实际底的比是( ),我们把这个比叫做( );这个比还和( )和( )的比相等,组成的比例是( )。1.2m0.8m1:40比例尺图上的高实际的高3:120=2:80注意变量和常量: 例:将一个平行四边形往外拉,如下图所示,在变化过程中,下列说法正确的有( )。
①平行四边形的周长是常量。
②平行四边形的底和高是变量,底随着高的减少而增加。
③平行四边形的面积和高是变量,面积随着高的减少而减少。
④长方形的底和高都是常量。与图形结合长方形面积的 =小长方形面积的S1×= S2 ×S1:S2 =12:512:5例:一个三角形分成两个小三角形(如右图,单位:厘米),
其中甲的底为8厘米,那么乙的底为( )厘米。
比与速度时间结合 1、甲、乙两人都从A地出发到B地,所用时间的比是4:5,则速度的比是( )。 2、甲乙两人步行的速度比是2:3,从A地到B地,甲走了21分钟,乙走了( )分钟.
A.31.5 B.28 C.14 D.10.5比例和方程和等式之间的联系。例:在①4×5=20,②4+x=30,③4:6= a:9,④5+b>7
这些子中,是等式的有( ),是方程的有( ),是比例的有( )。(填序号)①②③②③③ 5、比例的基本性质四、复习内容分析 在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。 提供了一种解比例的方法,原来用除法也可以解决。例: 25:7=X:35?????????= 0.8:1.2 解比例的方法就是应用比例的基本性质。四、复习内容分析比例尺数值比例尺线段比例尺比的形式分数形式图上距离实际距离=1 :100 ( )0 100 200 300千米实质上是一种比,是图上距离与实际距离的比。5、比例尺比例尺的类型题线段比例尺改写成数值比例尺
利用已知条件求比例尺
已知比例尺求图上距离或实际距离
应用比例尺画图
1.确定比例尺
2.根据比例尺求出图上距离
3.画图
4.标出实际距离和比例尺(1)画出下图中三角形按1:3的比缩小后的图形;
(2)画出下图中平行四边形形按2:1的比放大后的图形。 图形的放大与缩小1、图形的放大与缩小的特点:
形状相同,大小不同
2、图形的放大或缩小的方法:
一看,二算,三画四、复习内容分析6、正比例和反比例 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。用字母表示y/x=k(一定) 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。用字母表示x×y=k(一定) 判断下面各题中的两种量是不是成比例.如果
成比例,成什么比例. 1、收入一定,支出和结余。 2、出米率一定,稻谷的重量和大米的重量。 3、圆柱的侧面积一定,它的底面周长和高。 不成比例成正比例成反比例y=8x = 8 如果y=8x,x和y成( )比例。如果=和成( )比例y=Xy=8四、复习内容分析6、正比例和反比例 描述的是两种相关联的变量,他们的变化符合某种规律。 正比例符合两种变量的比值一定,反比例符合两种变量的积一定。 正比例和反比例的概念成为用比例知识解答应用题的基础。 小明带了60元钱去买笔记本,不同笔记本的单价和数量情况如下:其中广博这种笔记本的数量和总价如下: 从上表中可以知道:当钱数一定时,笔记本的单价和数量和成( );当购买同一种笔记本时,总价和数量成( ),小明最终选择了买广博笔记本,你觉得是ABCD中的( )种。反比例正比例C四、复习内容分析 7、正比例和反比例应用题。 用比例知识解答应用题的关键,是判断题中的数量是不是成比例,成什么比例。根据题中的比例关系,找出等量关系,再把其中未知数用 x 代替,列出方程解答。 四、复习内容分析 8、不同的知识灵活地解答应用题。 。 根据比与除法、分数之间的关系,再把比转化成分数或倍数来表示,沟通知识间的联系。根据它们之间的关系可以用不同的方法解答应用题,引导学生灵活运用知识解答应用题。 用不同的知识灵活地解答应用题 例1:少先队员在山坡上栽种松树和柏树,一共栽种了120棵,松树的棵数是柏树的4倍。松树和柏树各栽多少棵? (1)因为:松树的棵数+柏树的棵数=120棵
所以:我们可以根据这个等式列方程解应用题.
解:设柏树种了X棵,列方程得:
120-24=96(棵)
解:设松树种了
棵,列方程得:
120-96=24(棵)
答:柏树种了24棵,松树种了96棵.松树:柏树:X棵X棵120棵(2)因为松树的棵树是柏树的4倍,所以松树和
柏树棵树的比是4∶1.所以根据转化的比的关系,
可以用按比分配的知识来解答.
4+1=5
120× =96(棵)
120×
=24(棵)
答:柏树种了24棵,松树种了96棵. (3)因为松树的棵树是柏树的4倍,所以松树和柏树棵树的和是柏树棵树的5倍,根据倍数的数量关系可以运用算术方法解题.
120÷(4+1)=24(棵)
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.松树:柏树:“1”120棵120棵 根据倍数的数量关系可以运用算术方法解题.
120÷(1+ )(4)因为松树的棵树是柏树的4倍,所以柏树的棵数
就是松树棵树的 。 如果把松树的棵数看作单位1,那么,120棵对应的率就是1+ 根据倍数的数量关系可以运用算术方法解题.
120÷(1+ )=96(棵)
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.(5)因为松树的棵树是柏树的4倍,所以松树和柏树棵树的
比是4∶1,松树和松树、柏树棵树和的比是1∶5,所以根据
转化的比的关系,我可以用比例的知识来解答.
解:设柏树有X棵。 棵.
X∶120=1∶5
5X=120×1
X=24 =120
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.4.请你以小组为单位,讨论、交流你最喜欢那种方法.
为什么?
5、提问:若把“4倍”改写成“1/4”“25%”“0.25”的计算方
法会是怎样呢?
让学生自己发现数字发生改变,数量关系不变,所以
计算方法还是一样的。
在我们解应用题时,一道应用题的数量关系,可以转
化成不同解决形式.在解答时,我们选择我们熟练、简便
的方法进行解答.五、复习课时的安排●比的意义和基本性质。按比例分配(1课时)●比例的意义和基本性质,解比例、比例尺(1课时)●正比例和反比例的概念和正、反比例应用题(1课时)●用不同知识灵活解答应用题 (1课时)六、教学设想及措施1、突出概念和性质的比较,拓宽学生的基础知识。 在复习比和比例的知识时,要突出比和比例意义的本质属性。 1、 比和比例的意义和基本性质两个数相除,又叫做两个数的比。
表示两个比相等的式子,叫做比例。0.9 :0.6 = 1.5前项后项比值5 : 6 = 20 : 24内项外项比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
在比例里,两个外项的
积等于两个内项的积.
化简比解比例
正、反比例的联系与区别两种相关联的量一种量增加(减少)另一种量也随着增加(减少)比值(一定)一种量增加(减少)另一种量也随着减少(增加)积(一定)xy=k(一定)六、教学设想及措施2、突出知识的联系和区别,完善学生的认知结构。 在重视知识纵向、横向联系的同时,还要注意各类知识的不同点,让学生通过比较加以区别,以防混淆。 例如:▲ 比和分数、除法之间的联系和区别▲用比和比例知识以及其他知识解应用题方法的联系和区别▲数值比例尺和线段比例尺的联系和区别六、教学设想及措施3、突出解题方法的对比训练,培养学生的分析能力。 复习课,重在学生对解决数学问题的方法掌握,而不在于大量的习题练习。 ▲反比例和归总应用题的解题方法对比。 ▲化简比和求比值的方法对比▲判断正比例和反比例的方法对比▲求比例尺里三种类型问题的解题方法对比▲正比例应用题和归一应用题的解题方法对比六、教学设想及措施4、突出习题的变式训练,提高学生的应用能力。 我们要善于分析教材中的习题,练习时既要依据教材,又要跳出教材,设计新颖有趣的变式习题,加强知识在实际情境和生活中的应用。 一种药水是由药液和水按1:150配制而成,那么药液与药水的比是多少?水与药水的比是多少?六、教学设想及措施4、突出习题的变式训练,提高学生的应用能力。 如果有1510克药液,需要多少克水来配制?可配制这种药水多少克?
如果有1510克水,需要多少克药液来配制?可配制这种药水多少克?
如果配制1510克这种药水,需水和药液各多少克?药液 :水 = 1 :150 1 150 药水: 151 如果有1510克药液,需要多少克水来配制?可配制这种药水多少克?
1510克 X克药液 :水 = 1 :150 1 150 药水: 151 X克 1510克 如果有1510克水,需要多少克药液来配制?可配制这种药水多少克?
药液 :水 = 1 :150 1 150 药水: 151
1510克如果配制1510克这种药水,需水和药液各多少克?①男生人数与女生人数比是( )﹕( )
②男生人数与女生人数比是( )﹕( )
③男生人数是女生人数的几分之几?
④女生人数是男生人数的几分之几?
⑤男生人数是男、女生总人数的几分之几?
⑥女生人数是男、女生总人数的几分之几?
⑦男生人数比女生人数少几分之几?
⑧女生人数比男生人数多( )%分率转化的变式练习:
如果男生人数的40﹪与女生人数的3/5相等,那么 4、突出习题的变式训练,提高学生的应用能力。六、教学设想及措施六、教学设想及措施5、突出一题多解的训练,加深学生对数量关系的认识。 一题多解,既能加深学生对数量关系的认识,进一步理解和掌握数学知识,又能促进学生更好地把握知识之间的联系,使之融为一体。 六、教学设想及措施5、突出一题多解的训练,加深学生对数量关系的认识。 李庄要筑一条1200米的道路,前3天完成了40﹪。照这样计算,筑这条路一共要用多少天? 解法一:1÷(40﹪÷3)=7.5(天)
解法二:3÷40﹪=7.5(天)
解法三:3 ﹕40﹪= x ﹕ 1 x=7.5(天)
解法四:1200÷(1200×40﹪÷3)=7.5(天)
解法五:1200×(1-40﹪)÷(1200×40﹪÷3)+3=7.5(天)“1”
1200米
40%已修米数工效一定“1”(总天数)40%(已修3天)工效一定要有正确的复习理念
讲究复习的策略 但愿我们的复习课,
充满着生长的力量!
难点:用不同方法灵活解答应用题。四、复习内容分析加强基本概念——使学生加深基本概念的认识 通过比较,沟通联系,明确区别 ——以防止知识的混淆 突出解题思路——以使学生掌握方法,提高解题能力。 利用知识之间的联系 ——帮助学生掌握不同的解题方法。 四、复习内容分析 1、比的概念●比的意义两个数相除又叫做两个数的比。●比值的概念比的前项除以后项所得的商,叫做比值。 例如: 5÷6 可记作 5∶6。 例如:5÷6 = →就是5:6的比值。——是借助于除法的概念建立的。比——表示两个数量之间的关系而且是相除关系。生活中比赛得分2 :1是不是比? 它不是比,它没有一种相除关系在里面,所以它可以用0 :0来表示,而比是不能用0作为后项。 例:一个平行四边形花坛,底是6米,高是4米,6÷4表示( ),这一关系还可以用( )来表示。6 :4四、复习内容分析引导学生思考并归纳比与除法和分数的关系 a :b = a÷b = (b≠0)比的前项相当于分数的分子和除式中的被除数;
比的后项相当于分数的分母和除式中的除数;
比值相当于分数的分数值和除式中的商 比、除法和分数的关系一种
关系被除数分子除号分数线除数分母商分
数
值一种
运算一个数
比值的意义:同类数量的比值:不同类数量的比值:能加单位不能加单位 例:两辆汽车在公路上行驶,甲车行了75千米,耗油10升,乙车行了60千米,耗油9升。75千米:10升=7.5千米/升表示甲车每升汽油能行7.5千米。60千米:75千米= ,表示乙车行的路程是甲车的 。——产生新的量。表示倍数关系或几分之几。四、复习内容分析2、比基本性质: 比的前项和后项同时乘上或者除以相同的数(0除外),比值不变,这叫做比的基本性质。作用: 1、化简比——能让复杂的比依据比的基本性质化简成简单整数比。如0.314:1.256=1:2,也为后面图形的放大和缩小做铺垫。2、求比值——有时候比除法计算简单。四、复习内容分析求比值和化简比 学生容易混淆发生错误 列表对比 引导弄清求比值和化简比的区别 根据比的意义,用前项除以后项。 是一个数,可以是整数、小数或分数。 根据比的基本性质,把比的前项和后项同时乘或除以相同的数(0除外)。 是一个比,它的前项和后项是互质数(两个互质的整数比)。四、复习内容分析 应用比的知识 计算按比例分配问题 引导学生思考按比例分配应用题的解题依据、解题思路和方法。 3、按比例分配问题:四、复习内容分析 在农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配的方法通常叫做按比例分配。
●特点:
已知总量和部分量的比,求各部分量是多少。
●解题方法:
先求总份数,再求个部分量占总量的几分之几,最后用总量乘以这个几分之几,求出个部分量。 例:周长32厘米,长和宽的比是5:3,面积多少平方厘米?
2:33:7例:将这两种浓缩液混在一起制成新的清洁液,那么这种新的清洁液中浓缩液是清洁液的百分之几?
(百分号前保留一位小数)250ml 500ml
2:33:7250ml 500ml浓缩液是清洁液的百分之几?250 x + 500 x =150(ml)150÷750×100% ≈33.3%250+500=750(ml)(百分号前保留一位小数) 例:3克的蚂蚁能搬动45克的物体;3吨的大象能拉动4.5吨的物体,蚂蚁和大象谁的力气大?(要求:用学过的知识说明你的观点,回答要全面) 从物体的重量与动物本身的重量的比或比值看是蚂蚁的力气大,但是如果从动物驮的物体的重量来看是大象的力气大。3:45 =1:15 或 45:3=15
3:4.5 =1:1.5 4.5:3=1.5黄金比我的上半身的高度是65cm,下半身高度是98cm。当一个人上半身的高度与下半身的比是0.618:1时,这个人身材看上去就很美。四、复习内容分析 4、比例的意义表示两个比相等的式子叫做比例。 与图形的放大和缩小联系比较紧密,图形放大和缩小的结果,就组成了比例。能组成比例的两个图形,形状相同,大小不同。 例:将上题中的平行四边形按照一定比例缩小,画在平面图上,量得图上平行四边形的底是3厘米,高是2厘米。那么图上平行四边形的底与实际底的比是( ),我们把这个比叫做( );这个比还和( )和( )的比相等,组成的比例是( )。1.2m0.8m1:40比例尺图上的高实际的高3:120=2:80注意变量和常量: 例:将一个平行四边形往外拉,如下图所示,在变化过程中,下列说法正确的有( )。
①平行四边形的周长是常量。
②平行四边形的底和高是变量,底随着高的减少而增加。
③平行四边形的面积和高是变量,面积随着高的减少而减少。
④长方形的底和高都是常量。与图形结合长方形面积的 =小长方形面积的S1×= S2 ×S1:S2 =12:512:5例:一个三角形分成两个小三角形(如右图,单位:厘米),
其中甲的底为8厘米,那么乙的底为( )厘米。
比与速度时间结合 1、甲、乙两人都从A地出发到B地,所用时间的比是4:5,则速度的比是( )。 2、甲乙两人步行的速度比是2:3,从A地到B地,甲走了21分钟,乙走了( )分钟.
A.31.5 B.28 C.14 D.10.5比例和方程和等式之间的联系。例:在①4×5=20,②4+x=30,③4:6= a:9,④5+b>7
这些子中,是等式的有( ),是方程的有( ),是比例的有( )。(填序号)①②③②③③ 5、比例的基本性质四、复习内容分析 在比例里,两个外项的积等于两个内项的积。这叫做比例的基本性质。 提供了一种解比例的方法,原来用除法也可以解决。例: 25:7=X:35?????????= 0.8:1.2 解比例的方法就是应用比例的基本性质。四、复习内容分析比例尺数值比例尺线段比例尺比的形式分数形式图上距离实际距离=1 :100 ( )0 100 200 300千米实质上是一种比,是图上距离与实际距离的比。5、比例尺比例尺的类型题线段比例尺改写成数值比例尺
利用已知条件求比例尺
已知比例尺求图上距离或实际距离
应用比例尺画图
1.确定比例尺
2.根据比例尺求出图上距离
3.画图
4.标出实际距离和比例尺(1)画出下图中三角形按1:3的比缩小后的图形;
(2)画出下图中平行四边形形按2:1的比放大后的图形。 图形的放大与缩小1、图形的放大与缩小的特点:
形状相同,大小不同
2、图形的放大或缩小的方法:
一看,二算,三画四、复习内容分析6、正比例和反比例 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,他们的关系叫做正比例关系。用字母表示y/x=k(一定) 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,这两种量就叫做成反比例的量,他们的关系叫做反比例关系。用字母表示x×y=k(一定) 判断下面各题中的两种量是不是成比例.如果
成比例,成什么比例. 1、收入一定,支出和结余。 2、出米率一定,稻谷的重量和大米的重量。 3、圆柱的侧面积一定,它的底面周长和高。 不成比例成正比例成反比例y=8x = 8 如果y=8x,x和y成( )比例。如果=和成( )比例y=Xy=8四、复习内容分析6、正比例和反比例 描述的是两种相关联的变量,他们的变化符合某种规律。 正比例符合两种变量的比值一定,反比例符合两种变量的积一定。 正比例和反比例的概念成为用比例知识解答应用题的基础。 小明带了60元钱去买笔记本,不同笔记本的单价和数量情况如下:其中广博这种笔记本的数量和总价如下: 从上表中可以知道:当钱数一定时,笔记本的单价和数量和成( );当购买同一种笔记本时,总价和数量成( ),小明最终选择了买广博笔记本,你觉得是ABCD中的( )种。反比例正比例C四、复习内容分析 7、正比例和反比例应用题。 用比例知识解答应用题的关键,是判断题中的数量是不是成比例,成什么比例。根据题中的比例关系,找出等量关系,再把其中未知数用 x 代替,列出方程解答。 四、复习内容分析 8、不同的知识灵活地解答应用题。 。 根据比与除法、分数之间的关系,再把比转化成分数或倍数来表示,沟通知识间的联系。根据它们之间的关系可以用不同的方法解答应用题,引导学生灵活运用知识解答应用题。 用不同的知识灵活地解答应用题 例1:少先队员在山坡上栽种松树和柏树,一共栽种了120棵,松树的棵数是柏树的4倍。松树和柏树各栽多少棵? (1)因为:松树的棵数+柏树的棵数=120棵
所以:我们可以根据这个等式列方程解应用题.
解:设柏树种了X棵,列方程得:
120-24=96(棵)
解:设松树种了
棵,列方程得:
120-96=24(棵)
答:柏树种了24棵,松树种了96棵.松树:柏树:X棵X棵120棵(2)因为松树的棵树是柏树的4倍,所以松树和
柏树棵树的比是4∶1.所以根据转化的比的关系,
可以用按比分配的知识来解答.
4+1=5
120× =96(棵)
120×
=24(棵)
答:柏树种了24棵,松树种了96棵. (3)因为松树的棵树是柏树的4倍,所以松树和柏树棵树的和是柏树棵树的5倍,根据倍数的数量关系可以运用算术方法解题.
120÷(4+1)=24(棵)
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.松树:柏树:“1”120棵120棵 根据倍数的数量关系可以运用算术方法解题.
120÷(1+ )(4)因为松树的棵树是柏树的4倍,所以柏树的棵数
就是松树棵树的 。 如果把松树的棵数看作单位1,那么,120棵对应的率就是1+ 根据倍数的数量关系可以运用算术方法解题.
120÷(1+ )=96(棵)
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.(5)因为松树的棵树是柏树的4倍,所以松树和柏树棵树的
比是4∶1,松树和松树、柏树棵树和的比是1∶5,所以根据
转化的比的关系,我可以用比例的知识来解答.
解:设柏树有X棵。 棵.
X∶120=1∶5
5X=120×1
X=24 =120
120-24=96(棵)
答:柏树种了24棵,松树种了96棵.4.请你以小组为单位,讨论、交流你最喜欢那种方法.
为什么?
5、提问:若把“4倍”改写成“1/4”“25%”“0.25”的计算方
法会是怎样呢?
让学生自己发现数字发生改变,数量关系不变,所以
计算方法还是一样的。
在我们解应用题时,一道应用题的数量关系,可以转
化成不同解决形式.在解答时,我们选择我们熟练、简便
的方法进行解答.五、复习课时的安排●比的意义和基本性质。按比例分配(1课时)●比例的意义和基本性质,解比例、比例尺(1课时)●正比例和反比例的概念和正、反比例应用题(1课时)●用不同知识灵活解答应用题 (1课时)六、教学设想及措施1、突出概念和性质的比较,拓宽学生的基础知识。 在复习比和比例的知识时,要突出比和比例意义的本质属性。 1、 比和比例的意义和基本性质两个数相除,又叫做两个数的比。
表示两个比相等的式子,叫做比例。0.9 :0.6 = 1.5前项后项比值5 : 6 = 20 : 24内项外项比的前项和后项同时乘上或者同时除以相同的数(0除外),比值不变.
在比例里,两个外项的
积等于两个内项的积.
化简比解比例
正、反比例的联系与区别两种相关联的量一种量增加(减少)另一种量也随着增加(减少)比值(一定)一种量增加(减少)另一种量也随着减少(增加)积(一定)xy=k(一定)六、教学设想及措施2、突出知识的联系和区别,完善学生的认知结构。 在重视知识纵向、横向联系的同时,还要注意各类知识的不同点,让学生通过比较加以区别,以防混淆。 例如:▲ 比和分数、除法之间的联系和区别▲用比和比例知识以及其他知识解应用题方法的联系和区别▲数值比例尺和线段比例尺的联系和区别六、教学设想及措施3、突出解题方法的对比训练,培养学生的分析能力。 复习课,重在学生对解决数学问题的方法掌握,而不在于大量的习题练习。 ▲反比例和归总应用题的解题方法对比。 ▲化简比和求比值的方法对比▲判断正比例和反比例的方法对比▲求比例尺里三种类型问题的解题方法对比▲正比例应用题和归一应用题的解题方法对比六、教学设想及措施4、突出习题的变式训练,提高学生的应用能力。 我们要善于分析教材中的习题,练习时既要依据教材,又要跳出教材,设计新颖有趣的变式习题,加强知识在实际情境和生活中的应用。 一种药水是由药液和水按1:150配制而成,那么药液与药水的比是多少?水与药水的比是多少?六、教学设想及措施4、突出习题的变式训练,提高学生的应用能力。 如果有1510克药液,需要多少克水来配制?可配制这种药水多少克?
如果有1510克水,需要多少克药液来配制?可配制这种药水多少克?
如果配制1510克这种药水,需水和药液各多少克?药液 :水 = 1 :150 1 150 药水: 151 如果有1510克药液,需要多少克水来配制?可配制这种药水多少克?
1510克 X克药液 :水 = 1 :150 1 150 药水: 151 X克 1510克 如果有1510克水,需要多少克药液来配制?可配制这种药水多少克?
药液 :水 = 1 :150 1 150 药水: 151
1510克如果配制1510克这种药水,需水和药液各多少克?①男生人数与女生人数比是( )﹕( )
②男生人数与女生人数比是( )﹕( )
③男生人数是女生人数的几分之几?
④女生人数是男生人数的几分之几?
⑤男生人数是男、女生总人数的几分之几?
⑥女生人数是男、女生总人数的几分之几?
⑦男生人数比女生人数少几分之几?
⑧女生人数比男生人数多( )%分率转化的变式练习:
如果男生人数的40﹪与女生人数的3/5相等,那么 4、突出习题的变式训练,提高学生的应用能力。六、教学设想及措施六、教学设想及措施5、突出一题多解的训练,加深学生对数量关系的认识。 一题多解,既能加深学生对数量关系的认识,进一步理解和掌握数学知识,又能促进学生更好地把握知识之间的联系,使之融为一体。 六、教学设想及措施5、突出一题多解的训练,加深学生对数量关系的认识。 李庄要筑一条1200米的道路,前3天完成了40﹪。照这样计算,筑这条路一共要用多少天? 解法一:1÷(40﹪÷3)=7.5(天)
解法二:3÷40﹪=7.5(天)
解法三:3 ﹕40﹪= x ﹕ 1 x=7.5(天)
解法四:1200÷(1200×40﹪÷3)=7.5(天)
解法五:1200×(1-40﹪)÷(1200×40﹪÷3)+3=7.5(天)“1”
1200米
40%已修米数工效一定“1”(总天数)40%(已修3天)工效一定要有正确的复习理念
讲究复习的策略 但愿我们的复习课,
充满着生长的力量!
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
