陕西省黄陵中学2016-2017学年高二(重点班)下学期第三学月考数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二(重点班)下学期第三学月考数学(理)试题 Word版含答案 | 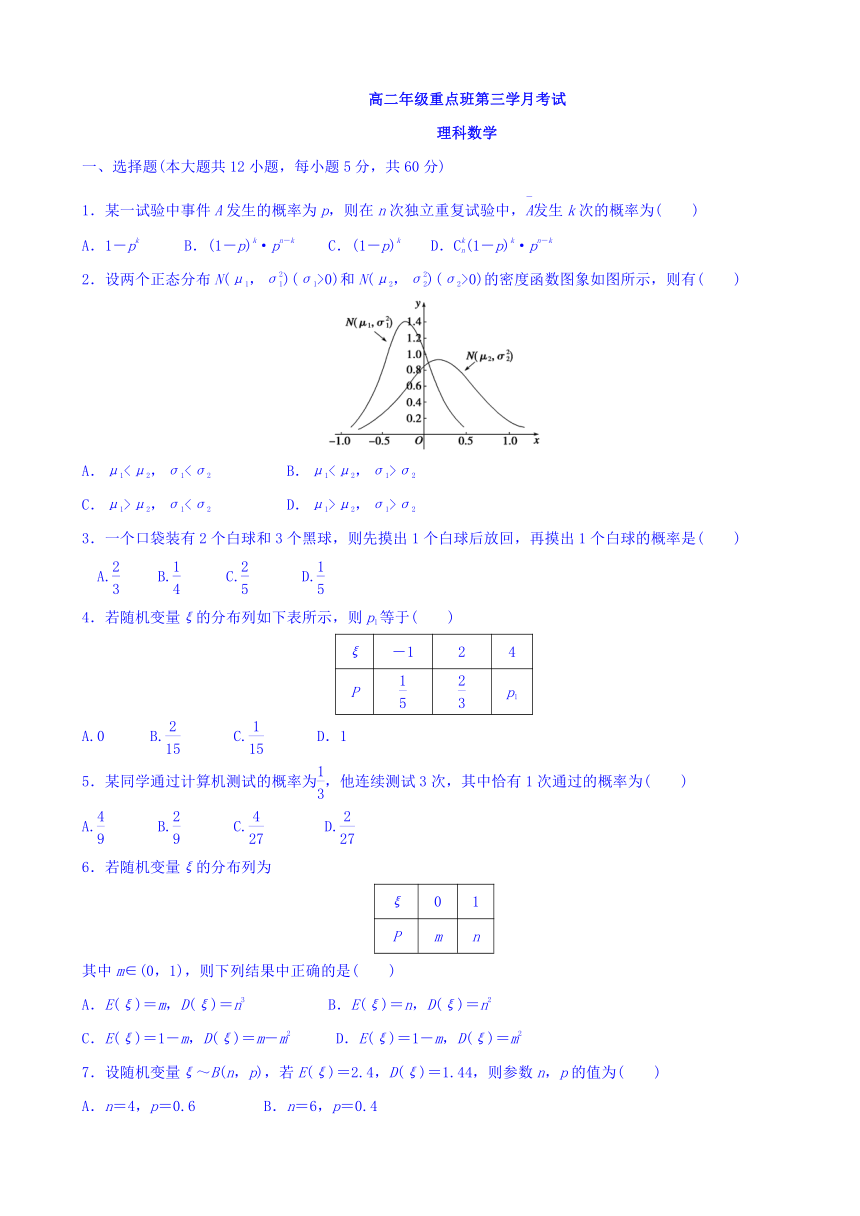 | |
| 格式 | zip | ||
| 文件大小 | 238.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-10 15:12:38 | ||
图片预览



文档简介
高二年级重点班第三学月考试
理科数学
一、选择题(本大题共12小题,每小题5分,共60分)
1.某一试验中事件A发生的概率为p,则在n次独立重复试验中,发生k次的概率为( )
A.1-pk
B.(1-p)k·pn-k
C.(1-p)k
D.C(1-p)k·pn-k
2.设两个正态分布N(μ1,σ)(σ1>0)和N(μ2,σ)(σ2>0)的密度函数图象如图所示,则有( )
A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1>σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2
3.一个口袋装有2个白球和3个黑球,则先摸出1个白球后放回,再摸出1个白球的概率是( )
A.
B.
C.
D.
4.若随机变量ξ的分布列如下表所示,则p1等于( )
ξ
-1
2
4
P
p1
A.0
B.
C.
D.1
5.某同学通过计算机测试的概率为,他连续测试3次,其中恰有1次通过的概率为( )
A.
B.
C.
D.
6.若随机变量ξ的分布列为
ξ
0
1
P
m
n
其中m∈(0,1),则下列结果中正确的是( )
A.E(ξ)=m,D(ξ)=n3
B.E(ξ)=n,D(ξ)=n2
C.E(ξ)=1-m,D(ξ)=m-m2
D.E(ξ)=1-m,D(ξ)=m2
7.设随机变量ξ~B(n,p),若E(ξ)=2.4,D(ξ)=1.44,则参数n,p的值为( )
A.n=4,p=0.6
B.n=6,p=0.4
C.n=8,p=0.3
D.n=24,p=0.1
盒中有1个黑球,9个白球,它们除颜色不同外,其他方面没什么差别,现由
10人依次摸出1个球后放回,设第1个人摸出黑球的概率是P1,第10个人摸
出黑球的概率是P10,则( )
A.P10=P1
B.P10=P1
C.P10=0
D.P10=P1
9.将一个骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
A.
B.
C.
D.
10.对标有不同编号的6件正品和4件次品的产品进行检测,不放回地依次摸出2件.在第一次摸出正品的条件下,第二次也摸到正品的概率是( )
A.
B.
C.
D.
11.甲、乙两工人在同样的条件下生产,日产量相等,每天出废品的情况如下表所列:
工人
甲
乙
废品数
0
1
2
3
0
1
2
3
概率
0.4
0.3
0.2
0.1
0.3
0.5
0.2
0
则有结论
( )
A.甲的产品质量比乙的产品质量好一些
B.乙的产品质量比甲的产品质量好一些
C.两人的产品质量一样好
D.无法判断谁的质量好一些
12.如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为
( )
A.0.504
B.0.994
C.0.496
D.0.06
二、填空题(本大题共4小题,每小题5分,共20分)
13.某大厦的一部电梯从底层出发后只能在第18,19,20层停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为,用X表示这5位乘客在第20层下电梯的人数,则P(X=4)=________.
14.已知随机变量ξ~B(5,),随机变量η=2ξ-1,则E(η)=________.
15.设离散型随机变量X~N(0,1),则P(X≤0)=________;P(-216.在某次学校的游园活动中,高二(2)班设计了这样一个游戏:在一个纸箱里放进了5个红球和5个白球,这些球除了颜色不同外完全相同,一次性从中摸出5个球,摸到4个或4个以上红球即为中奖,则中奖的概率是________.(精确到0.001)
三、解答题(本大题共5小题,共50分)
17、中国乒乓球队备战里约奥运会热身赛暨选拔赛于2016年7月14日在山东威海开赛.种子选手与,,三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,获胜的概率分别为,,,且各场比赛互不影响.
(1)若至少获胜两场的概率大于,则入选征战里约奥运会的最终大名单,否则不予入选,问是否会入选最终的大名单?
(2)求获胜场数的分布列和数学期望.
18.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将4次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
(1)求小球落入A袋中的概率P(A);
(2)在容器入口处依次放入4个小球,记ξ为落入A袋中小球的个数,试求ξ=3的概率与ξ的数学期望E(ξ).
19.在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似地服从正态分布
N(70,100).已知成绩在90分以上(含90分)的学生有12人.
(1)试问此次参赛学生的总数约为多少人?
(2)若成绩在80分以上(含80分)为优,试问此次竞赛成绩为优的学生约为多少人?
20.
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准
备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另
外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮
料.若4杯都选对,则月工资定为3
500元;若4杯选对3杯,则月工资定为2
800元;否则月工资定为2
100元.令X表示此人选对A饮料的杯数.假设此人
对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的数学期望.
21.生产工艺工程中产品的尺寸偏差X(mm)~N(0,22),如果产品的尺寸与现实
的尺寸偏差的绝对值不超过4
mm的为合格品,求生产5件产品的合格率不小
于80%的概率.(精确到0.001)((0.954
4)5≈0.791
9;(0.954
4)4≈0.8297)
答案
一、选择题(本大题共12小题,每小题5分,共60分)
1. D
2.A
3.C
4.B
5.A
6.C
7.B
8.D
9.B
10.D
11.B
12.B
二、填空题(本大题共4小题,每小题5分,共20分)
13.
14.
15. 0.954
4
16.0.103
三、解答题本大题共6小题,共70分)
17、【答案】(1)会入选最终的大名单;(2)
(2)获胜场数的可能取值为0,1,2,3,则
,…………………………
…7分
…………………………………………………………………………………………………8分
…9分
………………………………………………10分
所以获胜场数的分布列为:
…………………………………………………………………………………………11分
数学期望为.……………………………………12分
18.解 (1)法一 记小球落入B袋中的概率为P(B),
则P(A)+P(B)=1.
由于小球每次遇到黑色障碍物时一直向左或者一直向右下落,小球将落入B袋,
∴P(B)=()3+()3=,
∴P(A)=1-=.
法二 由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时小球将落入A袋,
∴P(A)=C()3+C()3=.
(2)由题意:ξ~B(4,),
所以有P(ξ=3)=C()3()1=,
∴E(ξ)=4×=3.
19.解 (1)设参赛学生的成绩为X,因为X~N(70,100),所以μ=70,σ=10.
则P(X≥90)=P(X≤50)=
==×(1-0.954
4)
=0.022
8,12÷0.022
8≈526(人).
因此,此次参赛学生的总数约为526人.
(2)由P(X≥80)=P(X≤60)=
==×(1-0.682
6)
=0.158
7,得526×0.158
7≈83.
因此,此次竞赛成绩为优的学生约为83人.
20.解 (1)依题意知X所有可能取值为0,1,2,3,4,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
P(X=4)==.所以X的分布列为:
X
0
1
2
3
4
P
(2)令Y表示此员工的月工资,则Y的所有可能取值为2
100,2
800,3
500,则P(Y=3
500)=P(X=4)=,
P(Y=2
800)=P(X=3)=,
P(Y=2
100)=P(X≤2)=++=.
所以E(Y)=×3
500+×2
800+×2
100=2
280.所以此员工月工资的数学期望为2
280元.
21.解 由题意X~N(0,22),求得P(|X|≤4)=P(-4≤X≤4)=0.954
4.
设Y表示5件产品中合格品个数,则Y~B(5,0.954
4).
∴P(Y≥5×0.8)=P(Y≥4)=C×(0.954
4)4×0.045
6+C×(0.954
4)5≈0.189
2+0.791
9≈0.981.
故生产的5件产品的合格率不小于80%的概率为0.981.
理科数学
一、选择题(本大题共12小题,每小题5分,共60分)
1.某一试验中事件A发生的概率为p,则在n次独立重复试验中,发生k次的概率为( )
A.1-pk
B.(1-p)k·pn-k
C.(1-p)k
D.C(1-p)k·pn-k
2.设两个正态分布N(μ1,σ)(σ1>0)和N(μ2,σ)(σ2>0)的密度函数图象如图所示,则有( )
A.μ1<μ2,σ1<σ2
B.μ1<μ2,σ1>σ2
C.μ1>μ2,σ1<σ2
D.μ1>μ2,σ1>σ2
3.一个口袋装有2个白球和3个黑球,则先摸出1个白球后放回,再摸出1个白球的概率是( )
A.
B.
C.
D.
4.若随机变量ξ的分布列如下表所示,则p1等于( )
ξ
-1
2
4
P
p1
A.0
B.
C.
D.1
5.某同学通过计算机测试的概率为,他连续测试3次,其中恰有1次通过的概率为( )
A.
B.
C.
D.
6.若随机变量ξ的分布列为
ξ
0
1
P
m
n
其中m∈(0,1),则下列结果中正确的是( )
A.E(ξ)=m,D(ξ)=n3
B.E(ξ)=n,D(ξ)=n2
C.E(ξ)=1-m,D(ξ)=m-m2
D.E(ξ)=1-m,D(ξ)=m2
7.设随机变量ξ~B(n,p),若E(ξ)=2.4,D(ξ)=1.44,则参数n,p的值为( )
A.n=4,p=0.6
B.n=6,p=0.4
C.n=8,p=0.3
D.n=24,p=0.1
盒中有1个黑球,9个白球,它们除颜色不同外,其他方面没什么差别,现由
10人依次摸出1个球后放回,设第1个人摸出黑球的概率是P1,第10个人摸
出黑球的概率是P10,则( )
A.P10=P1
B.P10=P1
C.P10=0
D.P10=P1
9.将一个骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
A.
B.
C.
D.
10.对标有不同编号的6件正品和4件次品的产品进行检测,不放回地依次摸出2件.在第一次摸出正品的条件下,第二次也摸到正品的概率是( )
A.
B.
C.
D.
11.甲、乙两工人在同样的条件下生产,日产量相等,每天出废品的情况如下表所列:
工人
甲
乙
废品数
0
1
2
3
0
1
2
3
概率
0.4
0.3
0.2
0.1
0.3
0.5
0.2
0
则有结论
( )
A.甲的产品质量比乙的产品质量好一些
B.乙的产品质量比甲的产品质量好一些
C.两人的产品质量一样好
D.无法判断谁的质量好一些
12.如图所示,A,B,C表示3种开关,若在某段时间内它们正常工作的概率分别为0.9,0.8,0.7,那么此系统的可靠性为
( )
A.0.504
B.0.994
C.0.496
D.0.06
二、填空题(本大题共4小题,每小题5分,共20分)
13.某大厦的一部电梯从底层出发后只能在第18,19,20层停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为,用X表示这5位乘客在第20层下电梯的人数,则P(X=4)=________.
14.已知随机变量ξ~B(5,),随机变量η=2ξ-1,则E(η)=________.
15.设离散型随机变量X~N(0,1),则P(X≤0)=________;P(-2
三、解答题(本大题共5小题,共50分)
17、中国乒乓球队备战里约奥运会热身赛暨选拔赛于2016年7月14日在山东威海开赛.种子选手与,,三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,获胜的概率分别为,,,且各场比赛互不影响.
(1)若至少获胜两场的概率大于,则入选征战里约奥运会的最终大名单,否则不予入选,问是否会入选最终的大名单?
(2)求获胜场数的分布列和数学期望.
18.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将4次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.
(1)求小球落入A袋中的概率P(A);
(2)在容器入口处依次放入4个小球,记ξ为落入A袋中小球的个数,试求ξ=3的概率与ξ的数学期望E(ξ).
19.在某校举行的数学竞赛中,全体参赛学生的竞赛成绩近似地服从正态分布
N(70,100).已知成绩在90分以上(含90分)的学生有12人.
(1)试问此次参赛学生的总数约为多少人?
(2)若成绩在80分以上(含80分)为优,试问此次竞赛成绩为优的学生约为多少人?
20.
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准
备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另
外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮
料.若4杯都选对,则月工资定为3
500元;若4杯选对3杯,则月工资定为2
800元;否则月工资定为2
100元.令X表示此人选对A饮料的杯数.假设此人
对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的数学期望.
21.生产工艺工程中产品的尺寸偏差X(mm)~N(0,22),如果产品的尺寸与现实
的尺寸偏差的绝对值不超过4
mm的为合格品,求生产5件产品的合格率不小
于80%的概率.(精确到0.001)((0.954
4)5≈0.791
9;(0.954
4)4≈0.8297)
答案
一、选择题(本大题共12小题,每小题5分,共60分)
1. D
2.A
3.C
4.B
5.A
6.C
7.B
8.D
9.B
10.D
11.B
12.B
二、填空题(本大题共4小题,每小题5分,共20分)
13.
14.
15. 0.954
4
16.0.103
三、解答题本大题共6小题,共70分)
17、【答案】(1)会入选最终的大名单;(2)
(2)获胜场数的可能取值为0,1,2,3,则
,…………………………
…7分
…………………………………………………………………………………………………8分
…9分
………………………………………………10分
所以获胜场数的分布列为:
…………………………………………………………………………………………11分
数学期望为.……………………………………12分
18.解 (1)法一 记小球落入B袋中的概率为P(B),
则P(A)+P(B)=1.
由于小球每次遇到黑色障碍物时一直向左或者一直向右下落,小球将落入B袋,
∴P(B)=()3+()3=,
∴P(A)=1-=.
法二 由于小球每次遇到黑色障碍物时,有一次向左和两次向右或两次向左和一次向右下落时小球将落入A袋,
∴P(A)=C()3+C()3=.
(2)由题意:ξ~B(4,),
所以有P(ξ=3)=C()3()1=,
∴E(ξ)=4×=3.
19.解 (1)设参赛学生的成绩为X,因为X~N(70,100),所以μ=70,σ=10.
则P(X≥90)=P(X≤50)=
==×(1-0.954
4)
=0.022
8,12÷0.022
8≈526(人).
因此,此次参赛学生的总数约为526人.
(2)由P(X≥80)=P(X≤60)=
==×(1-0.682
6)
=0.158
7,得526×0.158
7≈83.
因此,此次竞赛成绩为优的学生约为83人.
20.解 (1)依题意知X所有可能取值为0,1,2,3,4,
P(X=0)==,P(X=1)==,
P(X=2)==,P(X=3)==,
P(X=4)==.所以X的分布列为:
X
0
1
2
3
4
P
(2)令Y表示此员工的月工资,则Y的所有可能取值为2
100,2
800,3
500,则P(Y=3
500)=P(X=4)=,
P(Y=2
800)=P(X=3)=,
P(Y=2
100)=P(X≤2)=++=.
所以E(Y)=×3
500+×2
800+×2
100=2
280.所以此员工月工资的数学期望为2
280元.
21.解 由题意X~N(0,22),求得P(|X|≤4)=P(-4≤X≤4)=0.954
4.
设Y表示5件产品中合格品个数,则Y~B(5,0.954
4).
∴P(Y≥5×0.8)=P(Y≥4)=C×(0.954
4)4×0.045
6+C×(0.954
4)5≈0.189
2+0.791
9≈0.981.
故生产的5件产品的合格率不小于80%的概率为0.981.
同课章节目录
