人教A版数学必修五1.1.1 正弦定理 课件 (共33张PPT)
文档属性
| 名称 | 人教A版数学必修五1.1.1 正弦定理 课件 (共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-10 15:25:12 | ||
图片预览



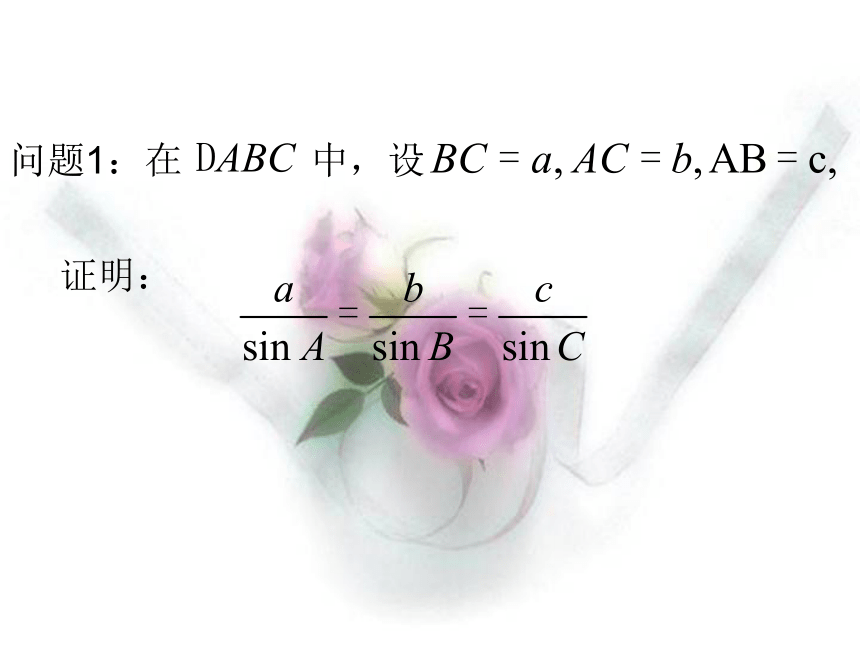



文档简介
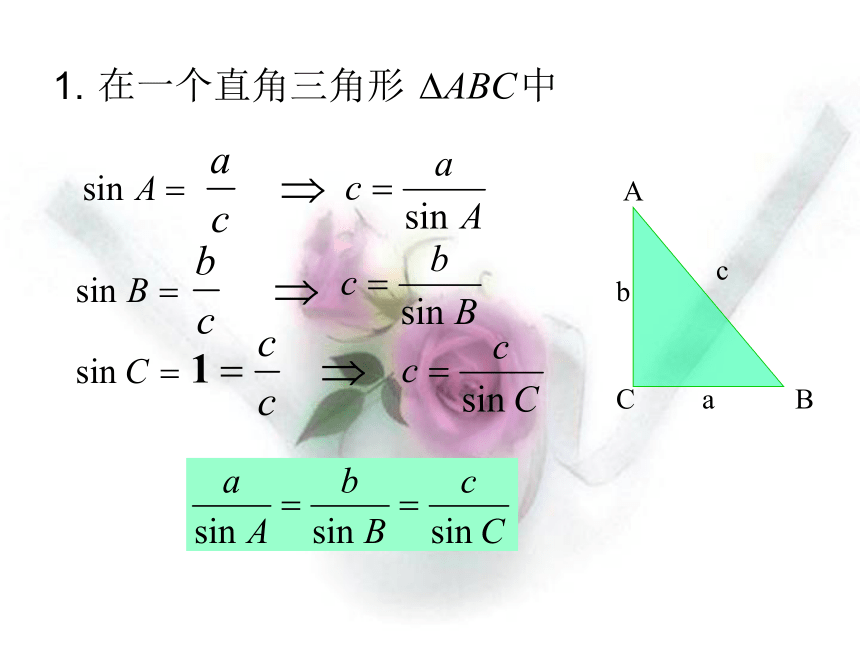
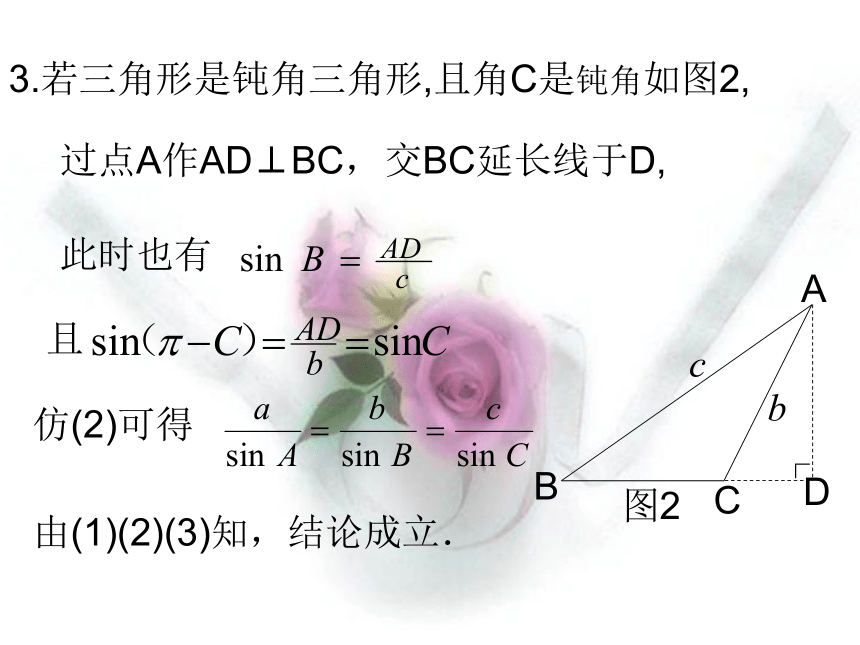
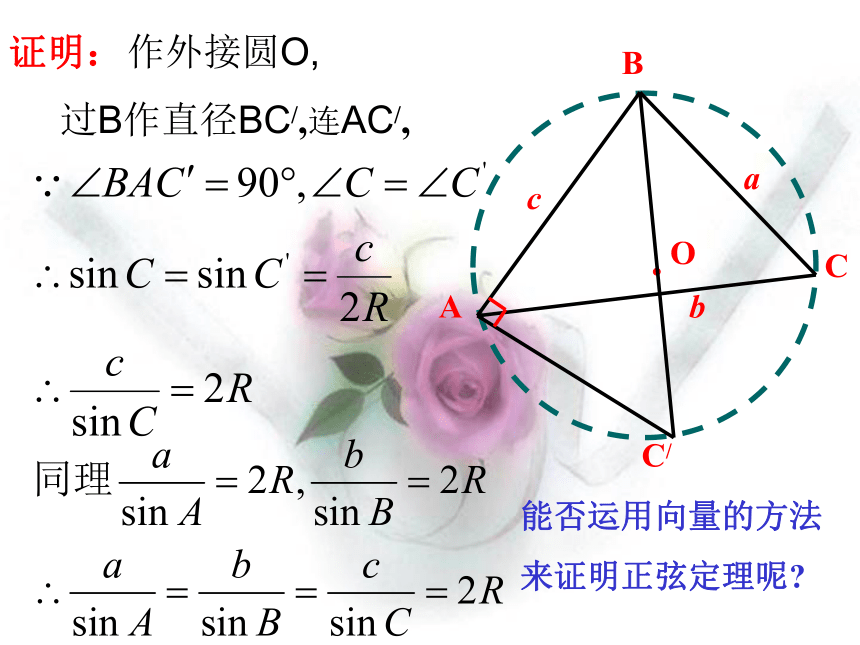
课件33张PPT。解三角形 定义:把三角形的三个角A,B,C和三条边a,b,c叫做三角形的元素,已知三角形的几个元素求其它元素的过程叫做解三角形。解三角形就是:由已知的边和角,求未知的边和角。正弦定理请你回顾一下:同一三角形中的边角关系知识回顾:a+b>c, a+c>b, b+c>a(1)三边:(2)三角:(3)边角:大边对大角课前检测在 中,求b , c ?证明:ACBcba所以AD=csinB=bsinC, 即同理可得过点A作AD⊥BC于D,此时有 2.若三角形是锐角三角形, 如图1,由(1)(2)(3)知,结论成立.3.若三角形是钝角三角形,且角C是钝角如图2, 交BC延长线于D,过点A作AD⊥BC,(1)文字叙述正弦定理:在一个三角形中,各边和它所对角 的正弦的比相等.(2)结构特点(3)方程的观点正弦定理实际上是已知其中三个,求另一个.能否运用向量的方法来证明正弦定理呢?和谐美、对称美.正弦定理:(2R为△ABC外接圆直径)=2R求证:4.有没有其他的方法证明以上的等式成立?证明:作外接圆O,过B作直径BC/,连AC/,能否运用向量的方法
来证明正弦定理呢?AcbCBDa向量法 利用向量的数量积,产生边的长与内角的三角函数的关系来证明.在直角三角形中在锐角三角形中由向量加法的三角形法则在钝角三角形中ABC具体证明过程
马上完成!You tryYou try正弦定理应用一:
已知两角和任意一边,求其余两边和一角
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解)
点拨:已知两角和任意一边,求其余两边和一角,
此时的解是唯一的.课堂练习:点拨:已知两边和其中一边的对角解三角形时,通常要用到三角形内角定理和定理或大边对大角定理等三角形有关性质.自我提高!
A、等腰三角形 B、直角三角形
C、等腰直角三角形 D、不能确定自我提高!
A、等腰三角形 B、直角三角形
C、等腰直角三角形 D、不能确定CCB
二种 —— 平面几何法 向量法定理应用方法 课时小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 作业:P 习题 1, 2, 4
来证明正弦定理呢?AcbCBDa向量法 利用向量的数量积,产生边的长与内角的三角函数的关系来证明.在直角三角形中在锐角三角形中由向量加法的三角形法则在钝角三角形中ABC具体证明过程
马上完成!You tryYou try正弦定理应用一:
已知两角和任意一边,求其余两边和一角
正弦定理应用二:
已知两边和其中一边对角,求另一边的对角,进
而可求其它的边和角。(要注意可能有两解)
点拨:已知两角和任意一边,求其余两边和一角,
此时的解是唯一的.课堂练习:点拨:已知两边和其中一边的对角解三角形时,通常要用到三角形内角定理和定理或大边对大角定理等三角形有关性质.自我提高!
A、等腰三角形 B、直角三角形
C、等腰直角三角形 D、不能确定自我提高!
A、等腰三角形 B、直角三角形
C、等腰直角三角形 D、不能确定CCB
二种 —— 平面几何法 向量法定理应用方法 课时小结二个 —— 已知两角和一边(只有一解)
已知两边和其中一边的对角
(有一解,两解,无解) 作业:P 习题 1, 2, 4
