人教版数学必修五1.1.2 余弦定理 课件 (共17张PPT)
文档属性
| 名称 | 人教版数学必修五1.1.2 余弦定理 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 845.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-10 15:27:26 | ||
图片预览






文档简介
课件17张PPT。第一章 三角公式及应用1.2.1 余弦定理授课班级:14普教
授课教师:郭清山
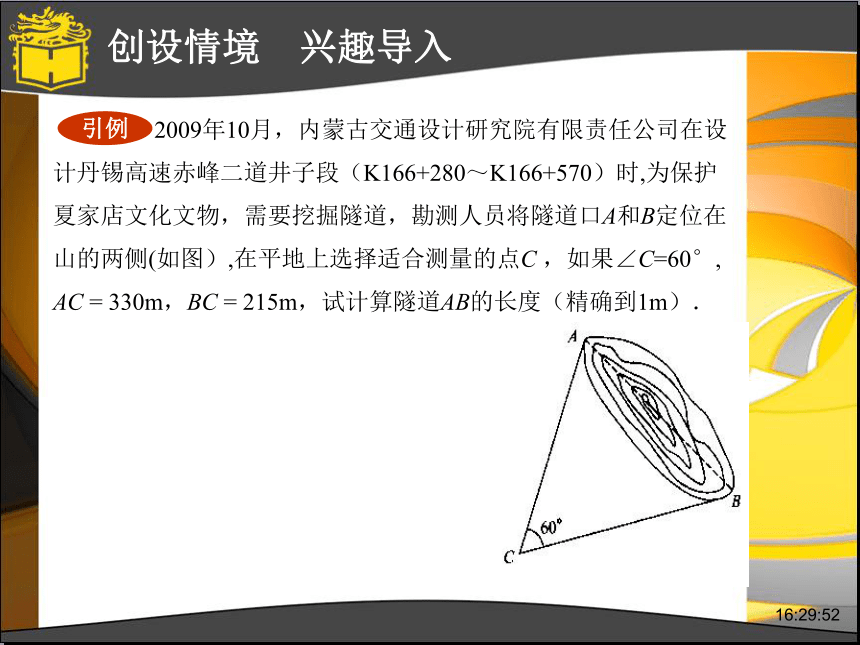
2016年11月6日21:40:40知识积累 复习巩固1、正弦二倍角公式2、余弦二倍角公式3、正切二倍角公式cos2α-sin2αcos2α=2cos2α-11-2sin2αsin2α=2sinαcosαtan2α=21:40:40创设情境 兴趣导入21:40:40创设情境 兴趣导入问题:如果知道三角形的两条边及它们的夹角,如何求第三条边呢?21:40:40动脑思考 探索新知在△ABC中(如图),我们用a,b,c分别表示∠A,∠B, ∠C可以证明,上述结论对于任意三角形都成立.于是得到余弦定理. 证明:a = b – c ,=b2 +c2-2bc cosA 即 a2=b2+c2-2bccosA的对边及其长度。21:40:40动脑思考 探索新知余弦定理 三角形任何一边的平方等于其它两边的平方和减去这两边的长与它们的夹角的余弦乘积的2倍. 即 (1.21) 是余弦定理的特例. 公式(1.21)经变形后可以写成 (1.22) 21:40:40动脑思考 探索新知利用余弦定理可以解决下列解三角形的问题: (1)已知三角形的两边及其夹角,求其它元素;(2)已知三角形的三边,求其它元素. 21:40:40解:巩固知识 典型例题∵ c2=a2+b2-2abcosC=63,查表或计算器可得∠A=40°54′.查表或计算器可得∠B=19°06′.21:40:40运用知识 强化练习解 : 在△ABC中,由余弦定理知 =84175. 所以 AB≈290m. 答:隧道AB的长度约为290m. =3302+2152-2×330×215×cos60°21:40:40运用知识 强化练习1.在△ABC中,a=35,b=24,∠C=60°,求c.73121:40:40解 :巩固知识 典型例题由余弦定理,得查表或计算器可得∠A=44°25′,∠B=101°32′,∠C=180°-∠A-∠B=34°3′.21:40:40运用知识 强化练习3.在△ABC中,a=2,b=5,c=4,求三个内角.∠A=78°8′
∠B=54°38′
∠C=47°14′∠A=22°20′
∠B=108°13′
∠C=49°27′4.在△ABC中,a=12,b=10,c=9,求三个内角.21:40:40拓展知识 联系实际约为12.12m.21:40:41归纳总结 理论升华21:40:41夜半偶句余弦定理考夹角,两边平方和求好;
减去倍乘抠塞角,三边平方见分晓。继续探索 活动探究21:40:41自我反思 目标检测21:40:41自我反思 目标检测21:40:41
授课教师:郭清山
2016年11月6日21:40:40知识积累 复习巩固1、正弦二倍角公式2、余弦二倍角公式3、正切二倍角公式cos2α-sin2αcos2α=2cos2α-11-2sin2αsin2α=2sinαcosαtan2α=21:40:40创设情境 兴趣导入21:40:40创设情境 兴趣导入问题:如果知道三角形的两条边及它们的夹角,如何求第三条边呢?21:40:40动脑思考 探索新知在△ABC中(如图),我们用a,b,c分别表示∠A,∠B, ∠C可以证明,上述结论对于任意三角形都成立.于是得到余弦定理. 证明:a = b – c ,=b2 +c2-2bc cosA 即 a2=b2+c2-2bccosA的对边及其长度。21:40:40动脑思考 探索新知余弦定理 三角形任何一边的平方等于其它两边的平方和减去这两边的长与它们的夹角的余弦乘积的2倍. 即 (1.21) 是余弦定理的特例. 公式(1.21)经变形后可以写成 (1.22) 21:40:40动脑思考 探索新知利用余弦定理可以解决下列解三角形的问题: (1)已知三角形的两边及其夹角,求其它元素;(2)已知三角形的三边,求其它元素. 21:40:40解:巩固知识 典型例题∵ c2=a2+b2-2abcosC=63,查表或计算器可得∠A=40°54′.查表或计算器可得∠B=19°06′.21:40:40运用知识 强化练习解 : 在△ABC中,由余弦定理知 =84175. 所以 AB≈290m. 答:隧道AB的长度约为290m. =3302+2152-2×330×215×cos60°21:40:40运用知识 强化练习1.在△ABC中,a=35,b=24,∠C=60°,求c.73121:40:40解 :巩固知识 典型例题由余弦定理,得查表或计算器可得∠A=44°25′,∠B=101°32′,∠C=180°-∠A-∠B=34°3′.21:40:40运用知识 强化练习3.在△ABC中,a=2,b=5,c=4,求三个内角.∠A=78°8′
∠B=54°38′
∠C=47°14′∠A=22°20′
∠B=108°13′
∠C=49°27′4.在△ABC中,a=12,b=10,c=9,求三个内角.21:40:40拓展知识 联系实际约为12.12m.21:40:41归纳总结 理论升华21:40:41夜半偶句余弦定理考夹角,两边平方和求好;
减去倍乘抠塞角,三边平方见分晓。继续探索 活动探究21:40:41自我反思 目标检测21:40:41自我反思 目标检测21:40:41
