2017-2018学年高一数学北师大版必修4学业分层测评:第1章 §1 周期现象 §2 角的概念的推广
文档属性
| 名称 | 2017-2018学年高一数学北师大版必修4学业分层测评:第1章 §1 周期现象 §2 角的概念的推广 |

|
|
| 格式 | zip | ||
| 文件大小 | 174.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-10 00:00:00 | ||
图片预览

文档简介
学业分层测评
(建议用时:45分钟)
[学业达标]
一、选择题
1.钟表分针的运动是一个周期现象,其周期为60分,现在分针恰好指在2点处,则100分钟后分针指在( )
A.8点处 B.10点处 C.11点处 D.12点处
【解析】 由题意知60分钟后分针仍指在2点处,100分钟后指在2+=10点处.
【答案】 B
2.集合M={x|x=
k·90°±45°,k∈Z
}与P={x|x=m·45°,m∈Z}之间的关系为( )A.MP
B.PM
C.M=P
D.M∩P=
【解析】 M={x|x=
k·90°±45°,k∈Z}
={x|x=2k·45°±45°,k∈±1)·45°,k∈Z}.
P={x|x=m·45°,m∈Z},故选A.
【答案】 A
3.若α是第二象限的角,则180°-α是( )
A.第一象限的角
B.第二象限的角
C.第三象限的角
D.第四象限的角
【解析】 α为第二象限的角,不妨设α=100°,则180°-α=180°-100°=80°为第一象限的角.
【答案】 A
4.与-457°角终边相同的角的集合是( )
A.{α|α=457°+k×360°,k∈Z}
B.{α|α=97°+k×360°,k∈Z}
C.{α|α=263°+k×360°,k∈Z}
D.{α|α=-263°+k×360°,k∈Z}
【解析】 在0°~360°内与-457°终边相同的角为-457°+2×360°=263°,故与-457°角终边相同的角的集合为{α|α=263°+k×360°,k∈Z}.【答案】 C
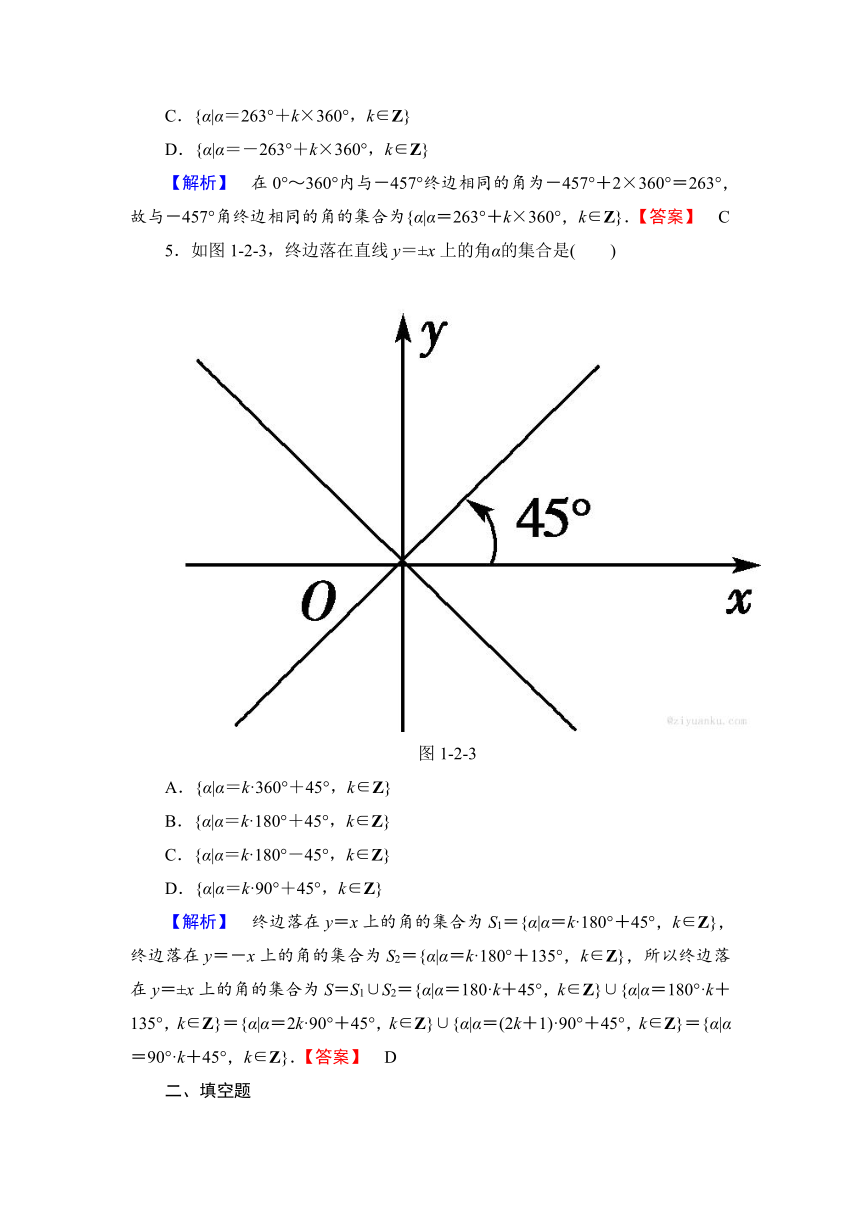
5.如图1 2 3,终边落在直线y=±x上的角α的集合是( )
图1 2 3
A.{α|α=k·360°+45°,k∈Z}
B.{α|α=k·180°+45°,k∈Z}
C.{α|α=k·180°-45°,k∈Z}
D.{α|α=k·90°+45°,k∈Z}
【解析】 终边落在y=x上的角的集合为S1={α|α=k·180°+45°,k∈Z},终边落在y=-x上的角的集合为S2={α|α=k·180°+135°,k∈Z},所以终边落在y=±x上的角的集合为S=S1∪S2={α|α=180·k+45°,k∈Z}∪{α|α=180°·k+135°,k∈Z}={α|α=2k·90°+45°,k∈Z}∪{α|α=(2k+1)·90°+45°,k∈Z}={α|α=90°·k+45°,k∈Z}.【答案】 D
二、填空题
6.与2
016°终边相同的最小正角是________,绝对值最小的角是________.
【解析】 2
016°=360°×5+216°,所以与2
016°终边相同的最小正角为216°.又2
016°=360°×6+(-144°),所以绝对值最小的角为-144°.
【答案】 216° -144°
7.设集合M={α|α=-36°+k×90°,k∈Z},N={α|-180°<α<180°},则M∩N=________.
【解析】 分别令k=-1,0,1,2,可得α=-126°,-36°,54°,144°.【答案】 {-126°,-36°,54°,144°}
8.终边落在阴影部分的角的集合是________.
图1 2 4
【解析】 终边落在OA上的角的集合为k·360°-45°,终边落在OB上的角的集合为k·360°+120°,终边落在阴影部分的角的集合为{α|-45°+360°·k≤α≤120°+360°·k,k∈Z}.
【答案】 {α|-45°+360°·k≤α≤120°+360°·k,k∈Z}
三、解答题
9.在平面直角坐标系中,画出下列集合所表示的角的终边所在区域(用阴影表示).
(1){α|k·360°≤α≤135°+k·360°,k∈Z};
(2){α|k·180°≤α≤135°+k·180°,k∈Z}.
【解】 如图所示:
10.已知角α是第三象限角,求:
(1)角是第几象限的角;
(2)角2α终边的位置.
【解】 (1)因为k·360°+180°<α(2)因为k·360°+180°<α所以2k·360°+360°<2α<2k·360°+540°,k∈Z,则无论k取何整数,表示的角的终边都在x轴的上半平面,故2α的终边在x轴的上半平面.
[能力提升]
1.在直角坐标系中,若α与β的终边互相垂直,则α与β的关系为( )
A.β=α+90°
B.β=α±90°C.β=α+90°-k·360°,k∈Z
D.β=α±90°+k·360°,k∈Z
【解析】 ∵α与β的终边互相垂直,故β-α=±90°+k·360°,k∈Z,∴β=α±90°+k·360°,k∈Z.
【答案】 D
2.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一或二象限角
C.第一或三象限角
D.第一或四象限角
【解析】 由于角2α的终边在x轴的上方,所以k·360°<2α【答案】 C
3.设集合A={x|k·360°+60°【解析】 因为A={x|k·360°+60°【答案】 {x|k·360°+150°4.探索如图1 2 5所示呈现的规律,判断2
014至2
016箭头的方向是________.(填序号)
图1 2 5
【解析】 观察题图可知,0到4为一个周期,
则从2
014到2
016对应着2到3到4.
【答案】 ③
(建议用时:45分钟)
[学业达标]
一、选择题
1.钟表分针的运动是一个周期现象,其周期为60分,现在分针恰好指在2点处,则100分钟后分针指在( )
A.8点处 B.10点处 C.11点处 D.12点处
【解析】 由题意知60分钟后分针仍指在2点处,100分钟后指在2+=10点处.
【答案】 B
2.集合M={x|x=
k·90°±45°,k∈Z
}与P={x|x=m·45°,m∈Z}之间的关系为( )A.MP
B.PM
C.M=P
D.M∩P=
【解析】 M={x|x=
k·90°±45°,k∈Z}
={x|x=2k·45°±45°,k∈±1)·45°,k∈Z}.
P={x|x=m·45°,m∈Z},故选A.
【答案】 A
3.若α是第二象限的角,则180°-α是( )
A.第一象限的角
B.第二象限的角
C.第三象限的角
D.第四象限的角
【解析】 α为第二象限的角,不妨设α=100°,则180°-α=180°-100°=80°为第一象限的角.
【答案】 A
4.与-457°角终边相同的角的集合是( )
A.{α|α=457°+k×360°,k∈Z}
B.{α|α=97°+k×360°,k∈Z}
C.{α|α=263°+k×360°,k∈Z}
D.{α|α=-263°+k×360°,k∈Z}
【解析】 在0°~360°内与-457°终边相同的角为-457°+2×360°=263°,故与-457°角终边相同的角的集合为{α|α=263°+k×360°,k∈Z}.【答案】 C
5.如图1 2 3,终边落在直线y=±x上的角α的集合是( )
图1 2 3
A.{α|α=k·360°+45°,k∈Z}
B.{α|α=k·180°+45°,k∈Z}
C.{α|α=k·180°-45°,k∈Z}
D.{α|α=k·90°+45°,k∈Z}
【解析】 终边落在y=x上的角的集合为S1={α|α=k·180°+45°,k∈Z},终边落在y=-x上的角的集合为S2={α|α=k·180°+135°,k∈Z},所以终边落在y=±x上的角的集合为S=S1∪S2={α|α=180·k+45°,k∈Z}∪{α|α=180°·k+135°,k∈Z}={α|α=2k·90°+45°,k∈Z}∪{α|α=(2k+1)·90°+45°,k∈Z}={α|α=90°·k+45°,k∈Z}.【答案】 D
二、填空题
6.与2
016°终边相同的最小正角是________,绝对值最小的角是________.
【解析】 2
016°=360°×5+216°,所以与2
016°终边相同的最小正角为216°.又2
016°=360°×6+(-144°),所以绝对值最小的角为-144°.
【答案】 216° -144°
7.设集合M={α|α=-36°+k×90°,k∈Z},N={α|-180°<α<180°},则M∩N=________.
【解析】 分别令k=-1,0,1,2,可得α=-126°,-36°,54°,144°.【答案】 {-126°,-36°,54°,144°}
8.终边落在阴影部分的角的集合是________.
图1 2 4
【解析】 终边落在OA上的角的集合为k·360°-45°,终边落在OB上的角的集合为k·360°+120°,终边落在阴影部分的角的集合为{α|-45°+360°·k≤α≤120°+360°·k,k∈Z}.
【答案】 {α|-45°+360°·k≤α≤120°+360°·k,k∈Z}
三、解答题
9.在平面直角坐标系中,画出下列集合所表示的角的终边所在区域(用阴影表示).
(1){α|k·360°≤α≤135°+k·360°,k∈Z};
(2){α|k·180°≤α≤135°+k·180°,k∈Z}.
【解】 如图所示:
10.已知角α是第三象限角,求:
(1)角是第几象限的角;
(2)角2α终边的位置.
【解】 (1)因为k·360°+180°<α
[能力提升]
1.在直角坐标系中,若α与β的终边互相垂直,则α与β的关系为( )
A.β=α+90°
B.β=α±90°C.β=α+90°-k·360°,k∈Z
D.β=α±90°+k·360°,k∈Z
【解析】 ∵α与β的终边互相垂直,故β-α=±90°+k·360°,k∈Z,∴β=α±90°+k·360°,k∈Z.
【答案】 D
2.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一或二象限角
C.第一或三象限角
D.第一或四象限角
【解析】 由于角2α的终边在x轴的上方,所以k·360°<2α
3.设集合A={x|k·360°+60°
014至2
016箭头的方向是________.(填序号)
图1 2 5
【解析】 观察题图可知,0到4为一个周期,
则从2
014到2
016对应着2到3到4.
【答案】 ③
