甘肃省张掖市临泽县九年级数学下册1.2《30°,45°,60°角的三角函数值》教案(新版)北师大版
文档属性
| 名称 | 甘肃省张掖市临泽县九年级数学下册1.2《30°,45°,60°角的三角函数值》教案(新版)北师大版 |  | |
| 格式 | zip | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-10 13:35:59 | ||
图片预览

文档简介
《30°,45°,60°角的三角函数值》
一、教材分析
本节课是在学生已有的直角三角形有关知识的基础上,根据三角函数的定义,探究30°,45°,60°三个特殊角的三角函数值,要求能利用特殊角的三角函数值进行基本的运算,并能根据三角函数特殊值求出特殊角;能根据生活中一些较简单的实际问题抽象出一定的几何模型,并由抽象出来的几何模型进行分析和计算,得出实际问题中需要的结果,在教学中要进一步渗透三角函数中量与量之间的相互联系、以及相互转化的观点,培养学生观察、分析、比较、概括的思维能力.对已学习能力较高的学生要求很理解并掌握任意两个锐角互余时,正、余弦之间的关系和正切之间的关系,并能利用这一性质进行简单的三角变换或相应计算.
二、教学目标
知识目标
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理.进一步体会三角函数的意义.
2.能够进行30°,45°,60°角的三角函数值的计算.
3.能够根据30°,45°,60°的三角函数值说明相应的锐角的大小.
能力目标
1.经历探索30°,45°,60°角的三角函数值的过程,发展学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
情感目标
1.积极参与数学活动,对数学产生好奇心.培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重点
1.探索30°,45°,60°角的三角函数值.
2.能够进行含30°,45°,60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点:三角函数值的应用
三、教学过程
复习旧知
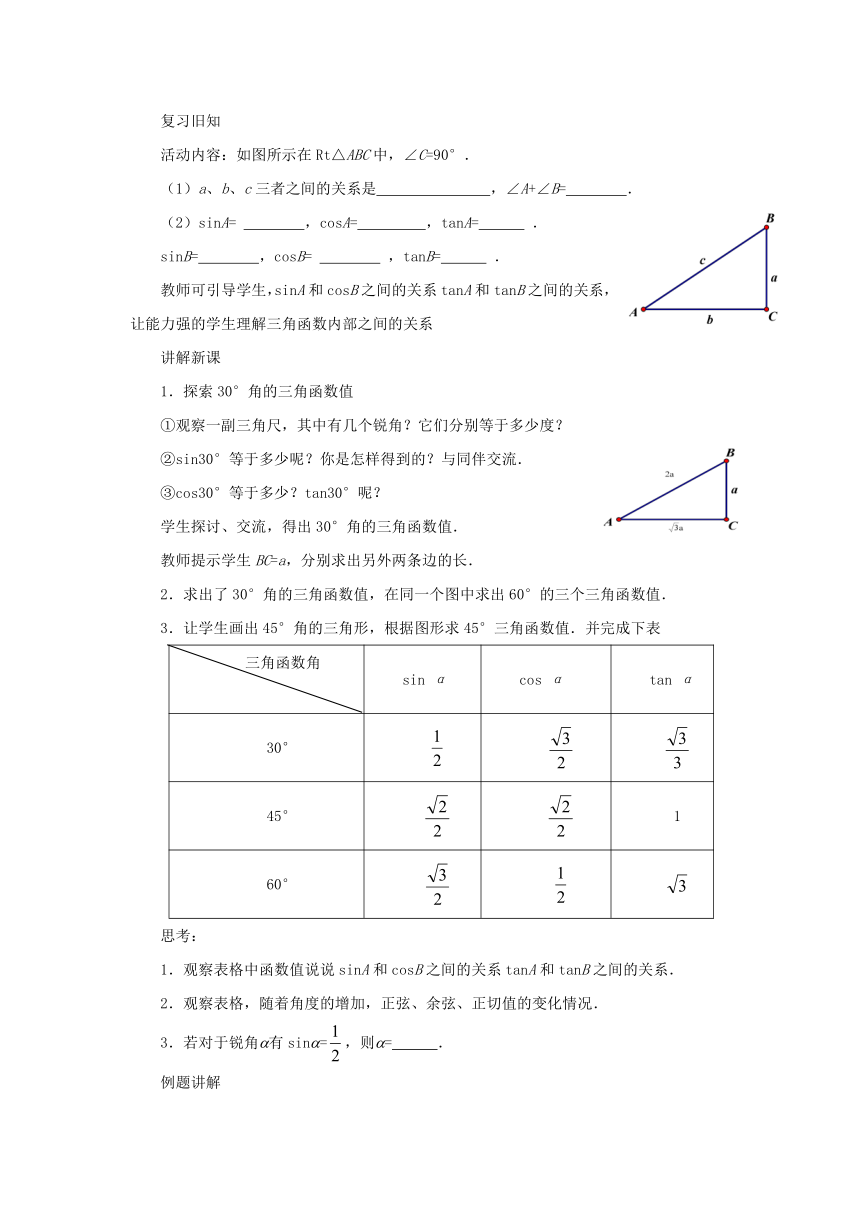
活动内容:如图所示在Rt△ABC中,∠C=90°.
(1)a、b、c三者之间的关系是
,∠A+∠B=
.
(2)sinA=
,cosA=
,tanA=
.
sinB=
,cosB=
,tanB=
.
教师可引导学生,sinA和cosB之间的关系tanA和tanB之间的关系,让能力强的学生理解三角函数内部之间的关系
讲解新课
1.探索30°角的三角函数值
①观察一副三角尺,其中有几个锐角?它们分别等于多少度?
②sin30°等于多少呢?你是怎样得到的?与同伴交流.
③cos30°等于多少?tan30°呢?
学生探讨、交流,得出30°角的三角函数值.
教师提示学生BC=a,分别求出另外两条边的长.
2.求出了30°角的三角函数值,在同一个图中求出60°的三个三角函数值.
3.让学生画出45°角的三角形,根据图形求45°三角函数值.并完成下表
三角函数角
sin
α
cos
α
tan
α
30°
45°
1
60°
思考:
1.观察表格中函数值说说sinA和cosB之间的关系tanA和tanB之间的关系.
2.观察表格,随着角度的增加,正弦、余弦、正切值的变化情况.
3.若对于锐角有sin=,则=
.
例题讲解
例1计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
解:(1)原式
(2)原式==0
基础练习
(1)sin60°-cos45°
(2)cos60°+tan60°
(3)
(4)
知识运用
例2:一个小孩荡秋千,秋千链子的长度为2.5
m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01
m)
目的
1.让学生能从实际问题中抽象出几何图形,利用几何图形解答实际问题
2.熟练30°、45°、60°角的三角函数值的计算.
巩固练习
1.某商场有一自动扶梯,其倾斜角为30°.高为7m,扶梯的长度是多少?
2.
如图,在Rt△ABC中,∠C=90°,∠A,∠B
,∠C的对边分别是a,b,c.
证明:sin2A+cos2A=1.
课堂小结
1.直角三角形三边的关系.
2.直角三角形两锐角的关系.
3.直角三角形边与角之间的关系.
4.特殊角30°,45°,60°角的三角函数值.
5.互余两角之间的三角函数关系.
6.同角之间的三角函数关系
课后作业
习题1.3
1、2、3、4
一、教材分析
本节课是在学生已有的直角三角形有关知识的基础上,根据三角函数的定义,探究30°,45°,60°三个特殊角的三角函数值,要求能利用特殊角的三角函数值进行基本的运算,并能根据三角函数特殊值求出特殊角;能根据生活中一些较简单的实际问题抽象出一定的几何模型,并由抽象出来的几何模型进行分析和计算,得出实际问题中需要的结果,在教学中要进一步渗透三角函数中量与量之间的相互联系、以及相互转化的观点,培养学生观察、分析、比较、概括的思维能力.对已学习能力较高的学生要求很理解并掌握任意两个锐角互余时,正、余弦之间的关系和正切之间的关系,并能利用这一性质进行简单的三角变换或相应计算.
二、教学目标
知识目标
1.经历探索30°,45°,60°角的三角函数值的过程,能够进行有关的推理.进一步体会三角函数的意义.
2.能够进行30°,45°,60°角的三角函数值的计算.
3.能够根据30°,45°,60°的三角函数值说明相应的锐角的大小.
能力目标
1.经历探索30°,45°,60°角的三角函数值的过程,发展学生观察、分析、发现的能力.
2.培养学生把实际问题转化为数学问题的能力.
情感目标
1.积极参与数学活动,对数学产生好奇心.培养学生独立思考问题的习惯.
2.在数学活动中获得成功的体验,锻炼克服困难的意志,建立自信心.
教学重点
1.探索30°,45°,60°角的三角函数值.
2.能够进行含30°,45°,60°角的三角函数值的计算.
3.比较锐角三角函数值的大小.
教学难点:三角函数值的应用
三、教学过程
复习旧知
活动内容:如图所示在Rt△ABC中,∠C=90°.
(1)a、b、c三者之间的关系是
,∠A+∠B=
.
(2)sinA=
,cosA=
,tanA=
.
sinB=
,cosB=
,tanB=
.
教师可引导学生,sinA和cosB之间的关系tanA和tanB之间的关系,让能力强的学生理解三角函数内部之间的关系
讲解新课
1.探索30°角的三角函数值
①观察一副三角尺,其中有几个锐角?它们分别等于多少度?
②sin30°等于多少呢?你是怎样得到的?与同伴交流.
③cos30°等于多少?tan30°呢?
学生探讨、交流,得出30°角的三角函数值.
教师提示学生BC=a,分别求出另外两条边的长.
2.求出了30°角的三角函数值,在同一个图中求出60°的三个三角函数值.
3.让学生画出45°角的三角形,根据图形求45°三角函数值.并完成下表
三角函数角
sin
α
cos
α
tan
α
30°
45°
1
60°
思考:
1.观察表格中函数值说说sinA和cosB之间的关系tanA和tanB之间的关系.
2.观察表格,随着角度的增加,正弦、余弦、正切值的变化情况.
3.若对于锐角有sin=,则=
.
例题讲解
例1计算:
(1)sin30°+cos45°;
(2)sin260°+cos260°-tan45°.
解:(1)原式
(2)原式==0
基础练习
(1)sin60°-cos45°
(2)cos60°+tan60°
(3)
(4)
知识运用
例2:一个小孩荡秋千,秋千链子的长度为2.5
m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差.(结果精确到0.01
m)
目的
1.让学生能从实际问题中抽象出几何图形,利用几何图形解答实际问题
2.熟练30°、45°、60°角的三角函数值的计算.
巩固练习
1.某商场有一自动扶梯,其倾斜角为30°.高为7m,扶梯的长度是多少?
2.
如图,在Rt△ABC中,∠C=90°,∠A,∠B
,∠C的对边分别是a,b,c.
证明:sin2A+cos2A=1.
课堂小结
1.直角三角形三边的关系.
2.直角三角形两锐角的关系.
3.直角三角形边与角之间的关系.
4.特殊角30°,45°,60°角的三角函数值.
5.互余两角之间的三角函数关系.
6.同角之间的三角函数关系
课后作业
习题1.3
1、2、3、4
