2017-2018学年高二数学人教A版选修2-2章末综合测评2 推理与证明
文档属性
| 名称 | 2017-2018学年高二数学人教A版选修2-2章末综合测评2 推理与证明 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-13 00:00:00 | ||
图片预览




文档简介
章末综合测评(二) 推理与证明
(时间120分钟,满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面四个推理不是合情推理的是( )
A.由圆的性质类比推出球的有关性质
B.由直角三角形、等腰三角形、等边三角形的内角和都是180°,归纳出所有三角形的内角和都是180°
C.某次考试张军的成绩是100分,由此推出全班同学的成绩都是100分
D.蛇、海龟、蜥蜴是用肺呼吸的,蛇、海龟、蜥蜴是爬行动物,所以所有的爬行动物都是用肺呼吸的
【解析】 逐项分析可知,A项属于类比推理,B项和D项属于归纳推理,而C项中各个学生的成绩不能类比,不是合情推理.
【答案】 C
2.下列几种推理是演绎推理的是( )
A.在数列{an}中,a1=1,an=(n≥2),由此归纳出{an}的通项公式
B.某校高三共有12个班,其中(1)班有55人,(2)班有54人,(3)班有52人,由此得出高三所有班级的人数都超过50人
C.由平面三角形的性质,推测出空间四面体的性质
D.两条直线平行,同旁内角互补.如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=π
【解析】 A,B为归纳推理,C为类比推理.
【答案】 D
3.下列推理是归纳推理的是( )
A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆
B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式C.由圆x2+y2=r2的面积πr2,猜出椭圆+=1的面积S=πab
D.科学家利用鱼的沉浮原理制造潜艇
【解析】 由归纳推理的特点知,选B.
【答案】 B
4.“凡是自然数都是整数,4是自然数,所以4是整数.”以上三段论推理( )
A.完全正确
B.推理形式不正确
C.不正确,两个“自然数”概念不一致
D.不正确,两个“整数”概念不一致
【解析】 大前提“凡是自然数都是整数”正确.小前提“4是自然数”也正确,推理形式符合演绎推理规则,所以结论正确.
【答案】 A
5.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用假设,应将5k+1-2k+1变形为( )
A.(5k-2k)+4×5k-2k
B.5(5k-2k)+3×2k
C.(5-2)(5k-2k)
D.2(5k-2k)-3×5k
【解析】 5k+1-2k+1=5k·5-2k·2=5k·5-2k·5+2k·5-2k·2=5(5k-2k)+3·2k.
【答案】 B
6.已知n为正偶数,用数学归纳法证明1-+-+…-=2时,若已假设n=k(k≥2且k为偶数)时等式成立,则还需要用归纳假设再证n=________时等式成立.( )
A.k+1
B.k+2
C.2k+2
D.2(k+2)
【解析】 根据数学归纳法的步骤可知,n=k(k≥2且k为偶数)的下一个偶数为n=k+2,故选B.
【答案】 B
7.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
A.28
B.76
C.123
D.199
【解析】 利用归纳法,a+b=1,a2+b2=3,a3+b3=4=3+1,a4+b4=4+3=7,a5+b5=7+4=11,a6+b6=11+7=18,a7+b7=18+11=29,a8+b8=29+18=47,a9+b9=47+29=76,a10+b10=76+47=123,规律为从第三组开始,其结果为前两组结果的和.
【答案】 C
8.分析法又叫执果索因法,若使用分析法证明:“设a>b>c,且a+b+c=0,求证:A.a-b>0
B.a-c>0
C.(a-b)(a-c)>0
D.(a-b)(a-c)<0
【解析】 因为a>b>c,且a+b+c=0,
所以3c0,c<0.
要证明0,只需证明2a+c>0(a>0,c<0,则a-c>0),只需证明a+c+(-b-c)>0,即证明a-b>0,这显然成立,故选A.
【答案】 A
9.在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19且n∈N
)成立,类比上述性质,在等比数列{bn}中,若b11=1,则有( )
A.b1·b2·…·bn=b1·b2·…·b19-n
B.b1·b2·…·bn=b1·b2·…·b21-n
C.b1+b2+…+bn=b1+b2+…+b19-n
D.b1+b2+…+bn=b1+b2+…+b21-n
【解析】 令n=10时,验证即知选B.
【答案】 B
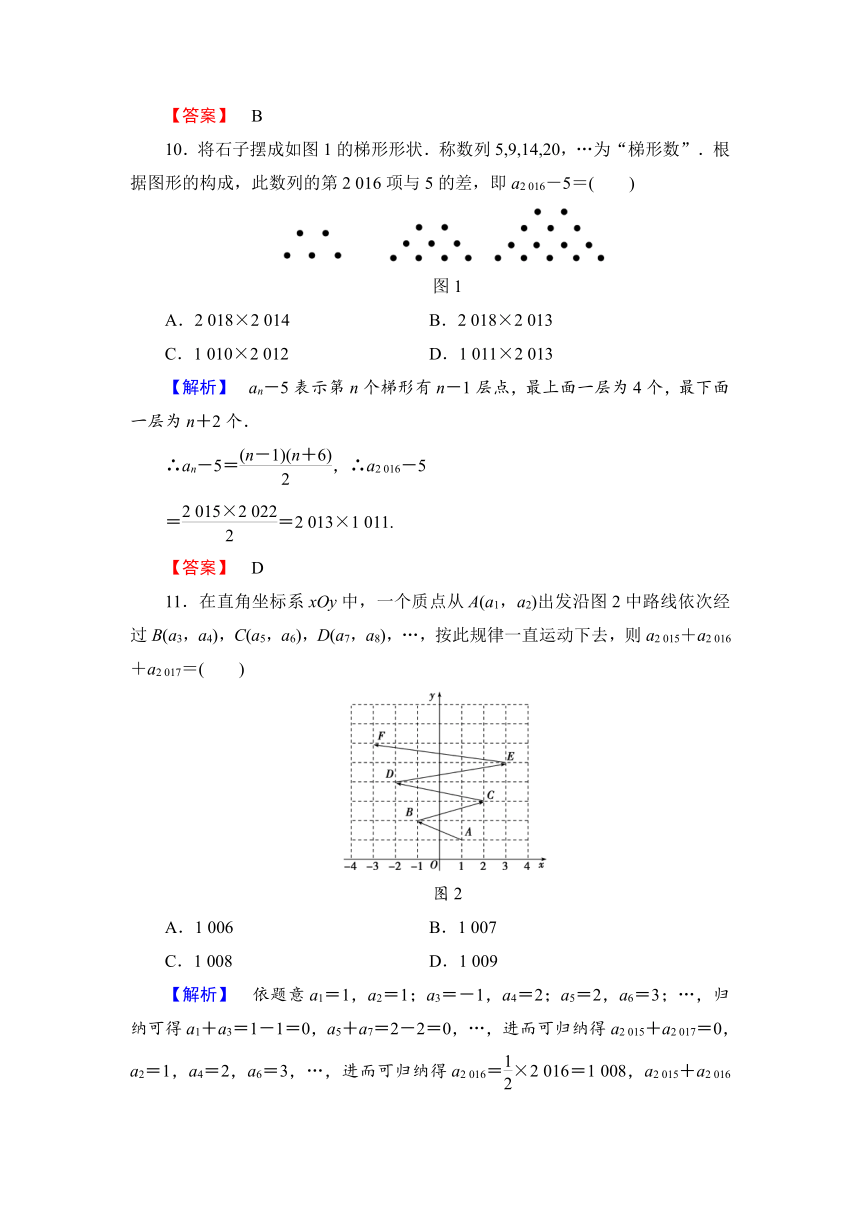
10.将石子摆成如图1的梯形形状.称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2
016项与5的差,即a2
016-5=( )
图1
A.2
018×2
014
B.2
018×2
013
C.1
010×2
012
D.1
011×2
013
【解析】 an-5表示第n个梯形有n-1层点,最上面一层为4个,最下面一层为n+2个.
∴an-5=,∴a2
016-5
==2
013×1
011.
【答案】 D
11.在直角坐标系xOy中,一个质点从A(a1,a2)出发沿图2中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此规律一直运动下去,则a2
015+a2
016+a2
017=( )
图2
A.1
006
B.1
007
C.1
008
D.1
009
【解析】 依题意a1=1,a2=1;a3=-1,a4=2;a5=2,a6=3;…,归纳可得a1+a3=1-1=0,a5+a7=2-2=0,…,进而可归纳得a2
015+a2
017=0,a2=1,a4=2,a6=3,…,进而可归纳得a2
016=×2
016=1
008,a2
015+a2
016+a2
017=1
008.故选C.
【答案】 C
12.记集合T={0,1,2,3,4,5,6,7,8,9},M=,将M中的元素按从大到小排列,则第2
016个数是( )
A.+++
B.+++
C.+++
D.+++
【解析】 因为+++
=(a1×103+a2×102+a3×101+a4),括号内表示的10进制数,其最大值为9
999,从大到小排列,第2
016个数为9
999-2
016+1=7
984,
所以a1=7,a2=9,a3=8,a4=4.【答案】 A
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.已知圆的方程是x2+y2=r2,则经过圆上一点M(x0,y0)的切线方程为x0x+y0y=r2.类比上述性质,可以得到椭圆+=1类似的性质为__________.
【解析】 圆的性质中,经过圆上一点M(x0,y0)的切线方程就是将圆的方程中的一个x与y分别用M(x0,y0)的横坐标与纵坐标替换.故可得椭圆+=1类似的性质为:过椭圆+=1上一点P(x0,y0)的切线方程为+=1.
【答案】 经过椭圆+=1上一点P(x0,y0)的切线方程为+=1
14.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是________
.
【解析】 依题意,把“整数对”的和相同的分为一组,不难得知第n组中每个“整数对”的和均为n+1,且第n组共有n个“整数对”,这样的前n组一共有个“整数对”,注意到<60<,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).
【答案】 (5,7)
15.当n=1时,有(a-b)(a+b)=a2-b2,当n=2时,有(a-b)(a2+ab+b2)=a3-b3,当n=3时,有(a-b)(a3+a2b+ab2+b3)=a4-b4,当n∈N
时,你能得到的结论是__________.
【解析】 根据题意,由于当n=1时,有(a-b)(a+b)=a2-b2,当n=2时,有(a-b)(a2+ab+b2)=a3-b3,
当n=3时,有(a-b)(a3+a2b+ab2+b3)=a4-b4,
当n∈N
时,左边第二个因式可知为an+an-1b+…+abn-1+bn,那么对应的表达式为(a-b)·(an+an-1b+…+abn-1+bn)=an+1-bn+1.
【答案】 (a-b)(an+an-1b+…+abn-1+bn)=an+1-bn+1
16.如图3,如果一个凸多面体是n(n∈N
)棱锥,那么这个凸多面体的所有顶点所确定的直线共有________条,这些直线共有f(n)对异面直线,则f(4)=________,f(n)=__________.(答案用数字或n的解析式表示)
图3
【解析】 所有顶点所确定的直线共有棱数+底边数+对角线数=n+n+=.从题图中能看出四棱锥中异面直线的对数为f(4)=4×2+×2=12,所以f(n)=n(n-2)+·(n-2)=.
【答案】 12
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)用综合法或分析法证明:
(1)如果a,b>0,则lg
≥;
(2)+>2+2.
【证明】 (1)当a,b>0时,有≥,
∴lg≥lg,
∴lg
≥lg
ab=.
(2)要证+>2+2,
只要证(+)2>(2+2)2,
即2>2,这是显然成立的,
所以,原不等式成立.
18.(本小题满分12分)观察以下各等式:
sin230°+cos260°+sin
30°cos
60°=,
sin220°+cos250°+sin
20°cos
50°=,
sin215°+cos245°+sin
15°cos
45°=.
分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性作出证明.
【解】 猜想:sin2α+cos2(α+30°)+sin
αcos(α+30°)=.
证明如下:
sin2α+cos2(α+30°)+sin
αcos(α+30°)
=sin2α++sin
α
=sin2α+cos2α-sin
αcos
α+sin2α+sin
α·cos
α-sin2α
=sin2α+cos2α
=.
19.(本小题满分12分)等差数列{an}的前n项和为Sn,a1=1+,S3=9+3.
(1)求数列{an}的通项an与前n项和Sn;
(2)设bn=(n∈N
),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
【解】 (1)由已知得∴d=2.
故an=2n-1+,Sn=n(n+).
(2)由(1)得bn==n+.
假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则b=bpbr,
即(q+)2=(p+)(r+),
∴(q2-pr)+(2q-p-r)=0,
∵p,q,r∈N
,
∴∴=pr,(p-r)2=0.
∴p=r,与p≠r矛盾.
∴数列{bn}中任意不同的三项都不可能成等比数列.
20.(本小题满分12分)点P为斜三棱柱ABC A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EF·cos∠DFE.扩展到空间类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
【解】 (1)因为PM⊥BB1,PN⊥BB1,又PM∩PN=P,
所以BB1⊥平面PMN,所以BB1⊥MN.
又CC1∥BB1,所以CC1⊥MN.
(2)在斜三棱柱ABC A1B1C1中,有S2=S2+S2-2SScos
α.
其中α为平面BCC1B1与平面ACC1A1所成的二面角.
证明如下:
因为CC1⊥平面PMN,所以上述的二面角的平面角为∠MNP.
在△PMN中,
因为PM2=PN2+MN2-2PN·MNcos∠MNP,
所以PM2·CC=PN2·CC+MN2·CC-2(PN·CC1)·(MN·CC1)cos∠MNP,
由于S=PN·CC1,S=MN·CC1,
S=PM·BB1=PM·CC1,
所以S2=S2+S2-2S·S·cos
α.
21.(本小题满分12分)如图4,在三棱锥P ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:
图4
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
【证明】 (1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.
又因为PA 平面DEF,DE 平面DEF,
所以直线PA∥平面DEF.
(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=PA=3,EF=BC=4.
又因为DF=5,故DF2=DE2+EF2,
所以∠DEF=90°,即DE⊥EF.
又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC 平面ABC,EF 平面ABC,
所以DE⊥平面ABC.
又DE 平面BDE,
所以平面BDE⊥平面ABC.
22.(本小题满分12分)在数列{an}中,a1=1,a2=,且an+1=(n≥2).
(1)求a3,a4,猜想an的表达式,并加以证明;
(2)设bn=,
求证:对任意的n∈N
,都有b1+b2+…+bn<.
【解】 (1)容易求得:a3=,a4=.
故可以猜想an=,n∈N
.
下面利用数学归纳法加以证明:
①显然当n=1,2,3,4时,结论成立,
②假设当n=k(k≥4,k∈N
)时,结论也成立,即
ak=.
那么当n=k+1时,由题设与归纳假设可知:
ak+1==
==
==.
即当n=k+1时,结论也成立,综上,对任意n∈N
,an=成立.
(2)bn=
=
==(-),
所以b1+b2+…+bn
=[(-1)+(-)+(-)+…+(-)]
=(-1),
所以只需要证明(-1)< <+1 3n+1<3n+2+1 0<2(显然成立),
所以对任意的n∈N
,都有b1+b2+…+bn<.
(时间120分钟,满分150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面四个推理不是合情推理的是( )
A.由圆的性质类比推出球的有关性质
B.由直角三角形、等腰三角形、等边三角形的内角和都是180°,归纳出所有三角形的内角和都是180°
C.某次考试张军的成绩是100分,由此推出全班同学的成绩都是100分
D.蛇、海龟、蜥蜴是用肺呼吸的,蛇、海龟、蜥蜴是爬行动物,所以所有的爬行动物都是用肺呼吸的
【解析】 逐项分析可知,A项属于类比推理,B项和D项属于归纳推理,而C项中各个学生的成绩不能类比,不是合情推理.
【答案】 C
2.下列几种推理是演绎推理的是( )
A.在数列{an}中,a1=1,an=(n≥2),由此归纳出{an}的通项公式
B.某校高三共有12个班,其中(1)班有55人,(2)班有54人,(3)班有52人,由此得出高三所有班级的人数都超过50人
C.由平面三角形的性质,推测出空间四面体的性质
D.两条直线平行,同旁内角互补.如果∠A和∠B是两条平行直线的同旁内角,则∠A+∠B=π
【解析】 A,B为归纳推理,C为类比推理.
【答案】 D
3.下列推理是归纳推理的是( )
A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆
B.由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式C.由圆x2+y2=r2的面积πr2,猜出椭圆+=1的面积S=πab
D.科学家利用鱼的沉浮原理制造潜艇
【解析】 由归纳推理的特点知,选B.
【答案】 B
4.“凡是自然数都是整数,4是自然数,所以4是整数.”以上三段论推理( )
A.完全正确
B.推理形式不正确
C.不正确,两个“自然数”概念不一致
D.不正确,两个“整数”概念不一致
【解析】 大前提“凡是自然数都是整数”正确.小前提“4是自然数”也正确,推理形式符合演绎推理规则,所以结论正确.
【答案】 A
5.用数学归纳法证明“5n-2n能被3整除”的第二步中,当n=k+1时,为了使用假设,应将5k+1-2k+1变形为( )
A.(5k-2k)+4×5k-2k
B.5(5k-2k)+3×2k
C.(5-2)(5k-2k)
D.2(5k-2k)-3×5k
【解析】 5k+1-2k+1=5k·5-2k·2=5k·5-2k·5+2k·5-2k·2=5(5k-2k)+3·2k.
【答案】 B
6.已知n为正偶数,用数学归纳法证明1-+-+…-=2时,若已假设n=k(k≥2且k为偶数)时等式成立,则还需要用归纳假设再证n=________时等式成立.( )
A.k+1
B.k+2
C.2k+2
D.2(k+2)
【解析】 根据数学归纳法的步骤可知,n=k(k≥2且k为偶数)的下一个偶数为n=k+2,故选B.
【答案】 B
7.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10=( )
A.28
B.76
C.123
D.199
【解析】 利用归纳法,a+b=1,a2+b2=3,a3+b3=4=3+1,a4+b4=4+3=7,a5+b5=7+4=11,a6+b6=11+7=18,a7+b7=18+11=29,a8+b8=29+18=47,a9+b9=47+29=76,a10+b10=76+47=123,规律为从第三组开始,其结果为前两组结果的和.
【答案】 C
8.分析法又叫执果索因法,若使用分析法证明:“设a>b>c,且a+b+c=0,求证:
B.a-c>0
C.(a-b)(a-c)>0
D.(a-b)(a-c)<0
【解析】 因为a>b>c,且a+b+c=0,
所以3c
要证明
【答案】 A
9.在等差数列{an}中,若a10=0,则有等式a1+a2+…+an=a1+a2+…+a19-n(n<19且n∈N
)成立,类比上述性质,在等比数列{bn}中,若b11=1,则有( )
A.b1·b2·…·bn=b1·b2·…·b19-n
B.b1·b2·…·bn=b1·b2·…·b21-n
C.b1+b2+…+bn=b1+b2+…+b19-n
D.b1+b2+…+bn=b1+b2+…+b21-n
【解析】 令n=10时,验证即知选B.
【答案】 B
10.将石子摆成如图1的梯形形状.称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2
016项与5的差,即a2
016-5=( )
图1
A.2
018×2
014
B.2
018×2
013
C.1
010×2
012
D.1
011×2
013
【解析】 an-5表示第n个梯形有n-1层点,最上面一层为4个,最下面一层为n+2个.
∴an-5=,∴a2
016-5
==2
013×1
011.
【答案】 D
11.在直角坐标系xOy中,一个质点从A(a1,a2)出发沿图2中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此规律一直运动下去,则a2
015+a2
016+a2
017=( )
图2
A.1
006
B.1
007
C.1
008
D.1
009
【解析】 依题意a1=1,a2=1;a3=-1,a4=2;a5=2,a6=3;…,归纳可得a1+a3=1-1=0,a5+a7=2-2=0,…,进而可归纳得a2
015+a2
017=0,a2=1,a4=2,a6=3,…,进而可归纳得a2
016=×2
016=1
008,a2
015+a2
016+a2
017=1
008.故选C.
【答案】 C
12.记集合T={0,1,2,3,4,5,6,7,8,9},M=,将M中的元素按从大到小排列,则第2
016个数是( )
A.+++
B.+++
C.+++
D.+++
【解析】 因为+++
=(a1×103+a2×102+a3×101+a4),括号内表示的10进制数,其最大值为9
999,从大到小排列,第2
016个数为9
999-2
016+1=7
984,
所以a1=7,a2=9,a3=8,a4=4.【答案】 A
二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)
13.已知圆的方程是x2+y2=r2,则经过圆上一点M(x0,y0)的切线方程为x0x+y0y=r2.类比上述性质,可以得到椭圆+=1类似的性质为__________.
【解析】 圆的性质中,经过圆上一点M(x0,y0)的切线方程就是将圆的方程中的一个x与y分别用M(x0,y0)的横坐标与纵坐标替换.故可得椭圆+=1类似的性质为:过椭圆+=1上一点P(x0,y0)的切线方程为+=1.
【答案】 经过椭圆+=1上一点P(x0,y0)的切线方程为+=1
14.已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是________
.
【解析】 依题意,把“整数对”的和相同的分为一组,不难得知第n组中每个“整数对”的和均为n+1,且第n组共有n个“整数对”,这样的前n组一共有个“整数对”,注意到<60<,因此第60个“整数对”处于第11组(每个“整数对”的和为12的组)的第5个位置,结合题意可知每个“整数对”的和为12的组中的各对数依次为:(1,11),(2,10),(3,9),(4,8),(5,7),…,因此第60个“整数对”是(5,7).
【答案】 (5,7)
15.当n=1时,有(a-b)(a+b)=a2-b2,当n=2时,有(a-b)(a2+ab+b2)=a3-b3,当n=3时,有(a-b)(a3+a2b+ab2+b3)=a4-b4,当n∈N
时,你能得到的结论是__________.
【解析】 根据题意,由于当n=1时,有(a-b)(a+b)=a2-b2,当n=2时,有(a-b)(a2+ab+b2)=a3-b3,
当n=3时,有(a-b)(a3+a2b+ab2+b3)=a4-b4,
当n∈N
时,左边第二个因式可知为an+an-1b+…+abn-1+bn,那么对应的表达式为(a-b)·(an+an-1b+…+abn-1+bn)=an+1-bn+1.
【答案】 (a-b)(an+an-1b+…+abn-1+bn)=an+1-bn+1
16.如图3,如果一个凸多面体是n(n∈N
)棱锥,那么这个凸多面体的所有顶点所确定的直线共有________条,这些直线共有f(n)对异面直线,则f(4)=________,f(n)=__________.(答案用数字或n的解析式表示)
图3
【解析】 所有顶点所确定的直线共有棱数+底边数+对角线数=n+n+=.从题图中能看出四棱锥中异面直线的对数为f(4)=4×2+×2=12,所以f(n)=n(n-2)+·(n-2)=.
【答案】 12
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)用综合法或分析法证明:
(1)如果a,b>0,则lg
≥;
(2)+>2+2.
【证明】 (1)当a,b>0时,有≥,
∴lg≥lg,
∴lg
≥lg
ab=.
(2)要证+>2+2,
只要证(+)2>(2+2)2,
即2>2,这是显然成立的,
所以,原不等式成立.
18.(本小题满分12分)观察以下各等式:
sin230°+cos260°+sin
30°cos
60°=,
sin220°+cos250°+sin
20°cos
50°=,
sin215°+cos245°+sin
15°cos
45°=.
分析上述各式的共同特点,猜想出反映一般规律的等式,并对等式的正确性作出证明.
【解】 猜想:sin2α+cos2(α+30°)+sin
αcos(α+30°)=.
证明如下:
sin2α+cos2(α+30°)+sin
αcos(α+30°)
=sin2α++sin
α
=sin2α+cos2α-sin
αcos
α+sin2α+sin
α·cos
α-sin2α
=sin2α+cos2α
=.
19.(本小题满分12分)等差数列{an}的前n项和为Sn,a1=1+,S3=9+3.
(1)求数列{an}的通项an与前n项和Sn;
(2)设bn=(n∈N
),求证:数列{bn}中任意不同的三项都不可能成为等比数列.
【解】 (1)由已知得∴d=2.
故an=2n-1+,Sn=n(n+).
(2)由(1)得bn==n+.
假设数列{bn}中存在三项bp,bq,br(p,q,r互不相等)成等比数列,则b=bpbr,
即(q+)2=(p+)(r+),
∴(q2-pr)+(2q-p-r)=0,
∵p,q,r∈N
,
∴∴=pr,(p-r)2=0.
∴p=r,与p≠r矛盾.
∴数列{bn}中任意不同的三项都不可能成等比数列.
20.(本小题满分12分)点P为斜三棱柱ABC A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EF·cos∠DFE.扩展到空间类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
【解】 (1)因为PM⊥BB1,PN⊥BB1,又PM∩PN=P,
所以BB1⊥平面PMN,所以BB1⊥MN.
又CC1∥BB1,所以CC1⊥MN.
(2)在斜三棱柱ABC A1B1C1中,有S2=S2+S2-2SScos
α.
其中α为平面BCC1B1与平面ACC1A1所成的二面角.
证明如下:
因为CC1⊥平面PMN,所以上述的二面角的平面角为∠MNP.
在△PMN中,
因为PM2=PN2+MN2-2PN·MNcos∠MNP,
所以PM2·CC=PN2·CC+MN2·CC-2(PN·CC1)·(MN·CC1)cos∠MNP,
由于S=PN·CC1,S=MN·CC1,
S=PM·BB1=PM·CC1,
所以S2=S2+S2-2S·S·cos
α.
21.(本小题满分12分)如图4,在三棱锥P ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:
图4
(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
【证明】 (1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.
又因为PA 平面DEF,DE 平面DEF,
所以直线PA∥平面DEF.
(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=PA=3,EF=BC=4.
又因为DF=5,故DF2=DE2+EF2,
所以∠DEF=90°,即DE⊥EF.
又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC 平面ABC,EF 平面ABC,
所以DE⊥平面ABC.
又DE 平面BDE,
所以平面BDE⊥平面ABC.
22.(本小题满分12分)在数列{an}中,a1=1,a2=,且an+1=(n≥2).
(1)求a3,a4,猜想an的表达式,并加以证明;
(2)设bn=,
求证:对任意的n∈N
,都有b1+b2+…+bn<.
【解】 (1)容易求得:a3=,a4=.
故可以猜想an=,n∈N
.
下面利用数学归纳法加以证明:
①显然当n=1,2,3,4时,结论成立,
②假设当n=k(k≥4,k∈N
)时,结论也成立,即
ak=.
那么当n=k+1时,由题设与归纳假设可知:
ak+1==
==
==.
即当n=k+1时,结论也成立,综上,对任意n∈N
,an=成立.
(2)bn=
=
==(-),
所以b1+b2+…+bn
=[(-1)+(-)+(-)+…+(-)]
=(-1),
所以只需要证明(-1)< <+1 3n+1<3n+2+1 0<2(显然成立),
所以对任意的n∈N
,都有b1+b2+…+bn<.
