山东省威海市乳山市实验中学2017年九年级(五四学制)6月月考数学试卷(含答案)
文档属性
| 名称 | 山东省威海市乳山市实验中学2017年九年级(五四学制)6月月考数学试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 302.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-14 00:00:00 | ||
图片预览

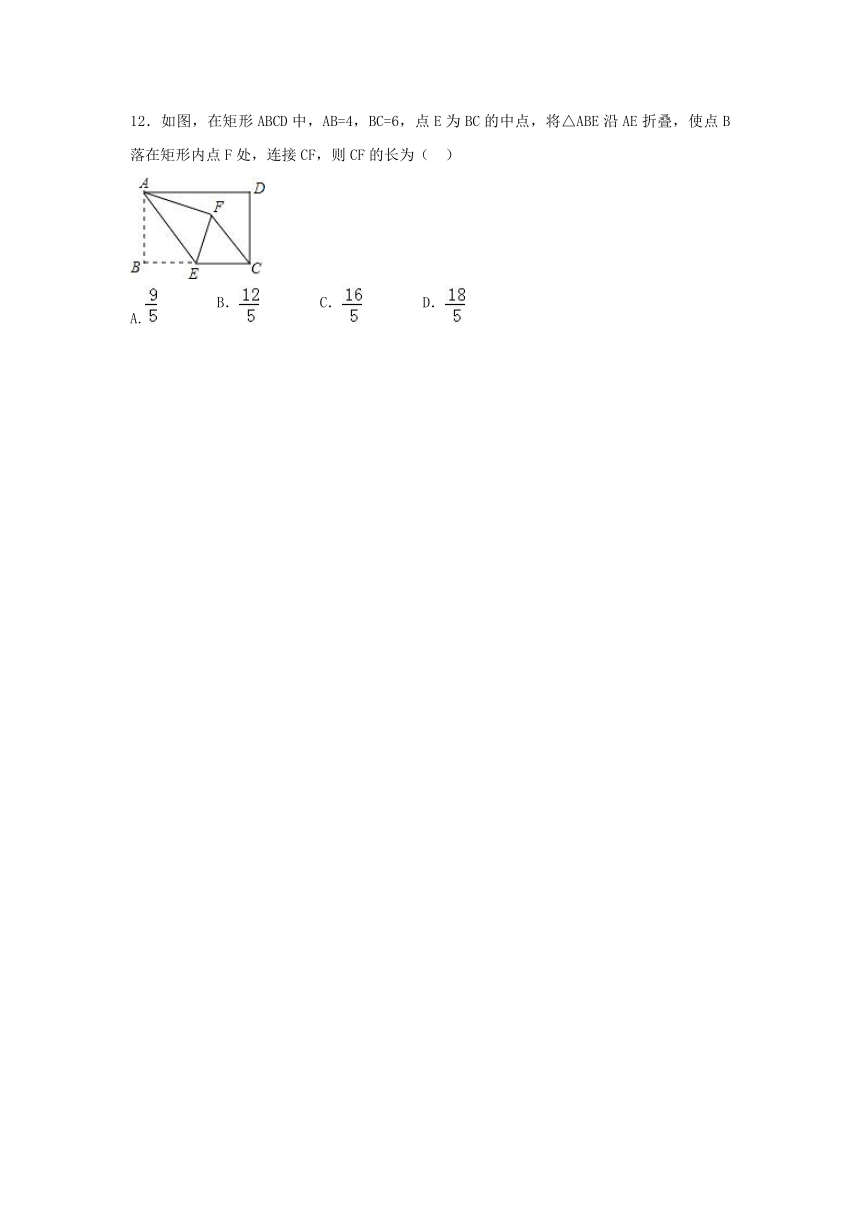

文档简介
山东省威海市乳山市实验中学2017届九年级(五四学制)6月月考数学试卷
第I卷(选择题)
评卷人
得分
一、选择题(题型注释)
1.若|a|=5,b=﹣3,则a﹣b=(
)
A.2或8
B.﹣2或8
C.2或﹣8
D.﹣2或﹣8
2.函数y=自变量x的取值范围为(
)
A.x>﹣1
B.x<﹣1
C.x≠﹣1
D.x≠0
3.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于(
)
A.35°
B.45°
C.55°
D.65°4.下列说法中,不正确的是(
)
A.如果a、b互为相反数,则a+b=0
B.a为任意有理数,则它的倒数为
C.的系数是
D.的算术平方根是3
5.若m、n(n<m)是关于x的一元二次方程1﹣(x﹣a)(x﹣b)=0的两个根,且b<a,则m,n,b,a的大小关系是(
)
A.m<a<b<n
B.a<m<n<b
C.b<n<m<a
D.n<b<a<m
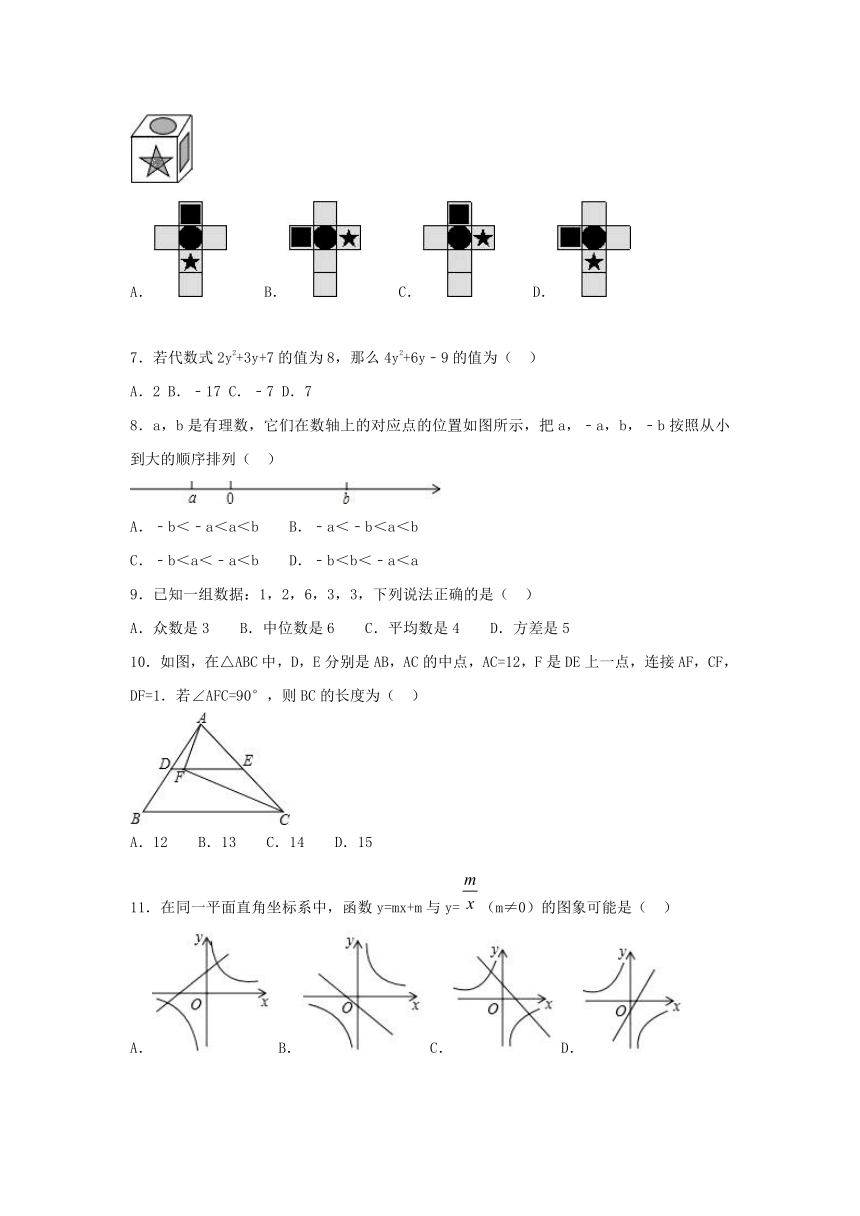
6.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是(
)
A.
B.
C.
D.
7.若代数式2y2+3y+7的值为8,那么4y2+6y﹣9的值为(
)
A.2
B.﹣17
C.﹣7
D.7
8.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,﹣a,b,﹣b按照从小到大的顺序排列(
)
A.﹣b<﹣a<a<b
B.﹣a<﹣b<a<b
C.﹣b<a<﹣a<b
D.﹣b<b<﹣a<a
9.已知一组数据:1,2,6,3,3,下列说法正确的是(
)
A.众数是3
B.中位数是6
C.平均数是4
D.方差是5
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为(
)
A.12
B.13
C.14
D.15
11.在同一平面直角坐标系中,函数y=mx+m与y=(m≠0)的图象可能是(
)
A.
B.
C.
D.
12.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为(
)
A.
B.
C.
D.
第II卷(非选择题)
评卷人
得分
二、填空题(题型注释)
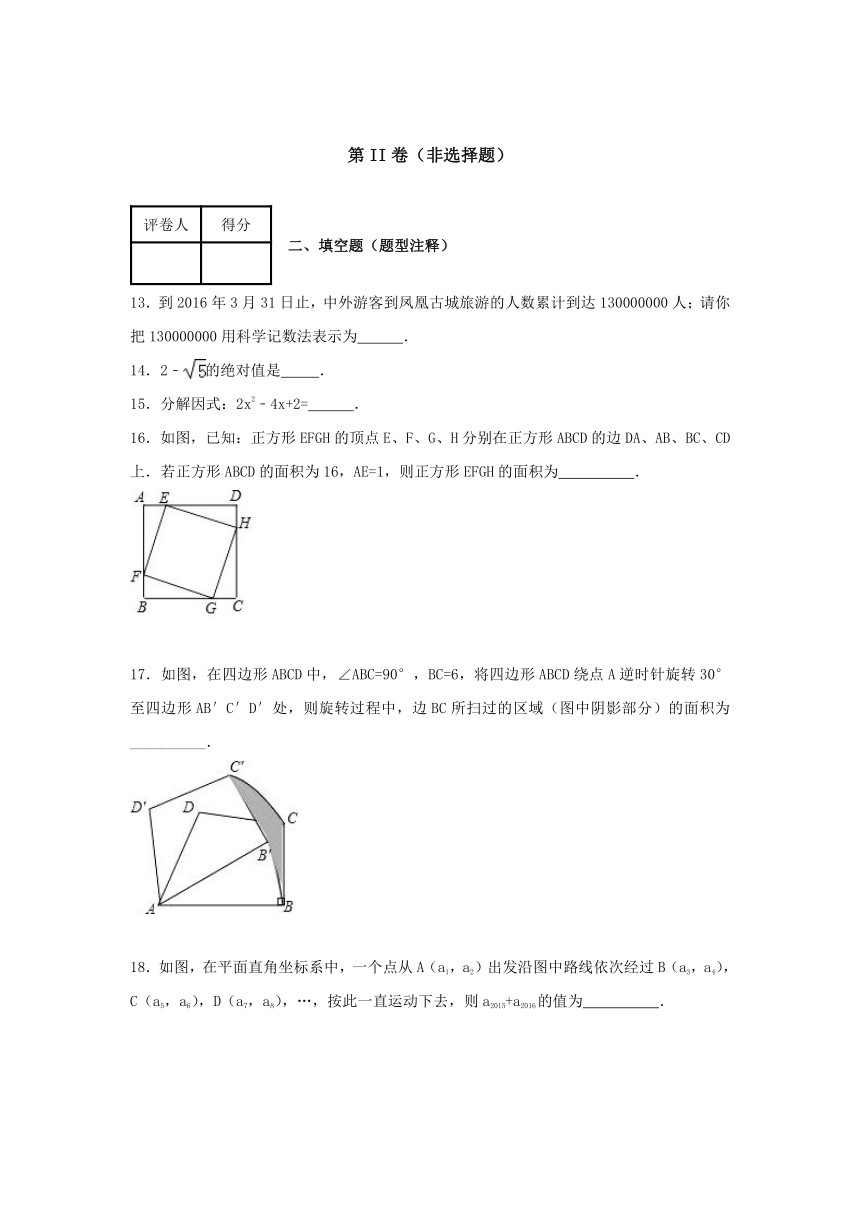
13.到2016年3月31日止,中外游客到凤凰古城旅游的人数累计到达130000000人;请你把130000000用科学记数法表示为
.
14.2﹣的绝对值是
.
15.分解因式:2x2﹣4x+2=
.
16.如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为
.
17.如图,在四边形ABCD中,∠ABC=90°,BC=6,将四边形ABCD绕点A逆时针旋转30°至四边形AB′C′D′处,则旋转过程中,边BC所扫过的区域(图中阴影部分)的面积为__________.
18.如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2015+a2016的值为
.
评卷人
得分
三、解答题(题型注释)
19.解不等式组:
20.(2015 安顺)“母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
21.甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
23.如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.24.已知:如图,在平行四边形ABCD
中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形
BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
25.在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
参考答案
1.B
【解析】
试题分析:首先由绝对值的性质,求得a的值,然后利用有理数的减法法则计算即可.
解:∵|a|=5,
∴a=±5.
当a=5时,a﹣b=5﹣(﹣3)=5+3=8;
当=﹣5时,a﹣b=﹣5﹣(﹣3)=﹣5+3=﹣2.
故选:B.
【点评】本题主要考查的是绝对值的性质和有理数的减法法则的应用,掌握有理数的减法法则是解题的关键.
2.C
【解析】
试题分析:根据分式有意义的条件,分母不为0,得出x的取值范围即可.
解:∵x+1≠0,
∴x≠﹣1,
∴函数y=自变量x的取值范围为x≠﹣1,
故选C.
【点评】本题考查了函数自变量的取值范围问题,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
3.C
【解析】
试题分析:由已知条件和观察图形,利用对顶角相等、角平分线的性质和垂直的定义,再结合平角为180度,就可求出角的度数.
解:∵∠B0C=∠AOD=70°,
又∵OE平分∠BOC,
∴∠BOE=∠BOC=35°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选C.
点评:本题利用垂直的定义,对顶角和角平分线的性质计算,要注意领会由垂直得直角这一要点.
4.B
【解析】
试题分析:应用排除法逐项分析即可.
解:A:根据有理数的加法法则:如果两个数互为相反数,那么它们的和为0,故选项A正确;
B:如果a为0,则它的倒数没有意义,故选项B错误;
C:单项式中的数字因数叫做单项式的系数,而π是数而不是字母,故是系数,即选项C正确;
D:因为,而9的算术平方根是3,故选项D正确;
故:选B
点评:本题考查了算术平方根、相反数、倒数、单项式,解题的关键是概念要清楚.
5.D.
【解析】
试题分析:如图抛物线y=(x﹣a)(x﹣b)与x轴交于点(a,0),(b,0),抛物线与直线y=1的交点为(n,1),(m,1),由图象可知,n<b<a<m.故选D.
考点:抛物线与x轴的交点.
6.C.
【解析】
试题分析:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图的位置正好相反,所以能得到的图形是C.故选C.
考点:几何体的展开图.
7.C
【解析】解:∵2y2+3y+7的值为8,
∴2y2+3y+7=8,
∴2y2+3y=1,
∴2(2y2+3y)=2=4y2+6y,
把4y2+6y=2代入4y2+6y﹣9得:
4y2+6y﹣9=2﹣9=﹣7.
故选C.
【点评】代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取代数式4y2+6y的值,然后利用“整体代入法”求代数式的值.8.C
【解析】
试题分析:利用有理数大小的比较方法可得﹣a<b,﹣b<a,b>0>a进而求解.
解:观察数轴可知:b>0>a,且b的绝对值大于a的绝对值.
在b和﹣a两个正数中,﹣a<b;在a和﹣b两个负数中,绝对值大的反而小,则﹣b<a.
因此,﹣b<a<﹣a<b.
故选:C.
【点评】有理数大小的比较方法:正数大于0;负数小于0;正数大于一切负数;两个负数,绝对值大的反而小.
9.A
【解析】
试题分析:利用众数、算术平均数、中位数及方差的定义分别求解后即可确定正确的选项.
解:A、数据3出现2次,最多,故众数为3,故A选项正确;
B、排序后位于中间位置的数为3,故中位数为3,故B选项错误;
C、平均数为3,故C选项错误;
D、方差为2.8,故D选项错误.
故选:A.点评:本题考查了众数、算术平均数、中位数及方差的定义,属于基础题,比较简单.
10.C
【解析】
试题分析:如图,首先证明EF=6,继而得到DE=7;证明DE为△ABC的中位线,即可解决问题.
解:如图,∵∠AFC=90°,AE=CE,
∴EF==6,DE=1+6=7;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=14,
故选C.
【点评】该题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题;牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键.
11.A
【解析】
试题分析:A、由函数y=mx+m的图象可知m>0,由函数y=的图象可知m>0,故A选项正确;
B、由函数y=mx+m的图象可知m<0,由函数y=的图象可知m>0,相矛盾,故B选项错误;
C、由函数y=mx+m的图象y随x的增大而减小,则m<0,而该直线与y轴交于正半轴,则m>0,相矛盾,故C选项错误;
D、由函数y=mx+m的图象y随x的增大而增大,则m>0,而该直线与y轴交于负半轴,则m<0,相矛盾,故D选项错误;
故选:A.
考点:反比例函数的图象;一次函数的图象
12.D.
【解析】
试题分析:如图,连接BF,已知BC=6,点E为BC的中点,可得BE=3,根据勾股定理求得AE=5,根据三角形的面积公式求出BH=,即可得BF=,因FE=BE=EC,可得∠BFC=90°,再由勾股定理可得CF=.
故答案选D.
考点:翻折变换;矩形的性质;勾股定理.13.1.3×108.
【解析】
试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:将13000
0000用科学记数法表示为1.3×108.
故答案为:1.3×108.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
14.﹣2.
【解析】
试题分析:先判断2﹣的正负值,再根据“正数的绝对值是它本身,负数的绝对值是其相反数”即可求解.
解:2﹣的绝对值是|2﹣|=﹣2.
故本题的答案﹣2.
点评:此题考查了绝对值的性质,要求掌握绝对值的性质及其定义,并能熟练运用到实际当中.
15.2(x﹣1)2.
【解析】
试题分析:先提取公因数2,再利用完全平方公式进行二次分解.完全平方公式:(a±b)2=a2±2ab+b2.
解:2x2﹣4x+2,
=2(x2﹣2x+1),
=2(x﹣1)2.
点评:本题主要考查提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
16.10
【解析】
试题分析:根据正方形的性质找出相等的边角关系,从而证出△AFE≌△BGF≌△CHG≌△DEH,再由正方形ABCD的面积为16,AE=1,找出AF的长度,根据S正方形EFGH=S正方形ABCD﹣4S△AFE即可得出结论.
解:∵四边形ABCD、EFGH均为正方形,
∴∠A=∠B=90°,∠EFG=90°,EF=FG.
∵∠AFE+∠BFG=90°,∠BFG+∠BGF=90°,
∴∠AFE=∠BGF.
在△AFE和△BGF中,,
∴△AFE≌△BGF(AAS),
∴BF=AE=1.
∵正方形ABCD的面积为16,
∴AB=4,AF=AB﹣BF=3.
同理可证出△AFE≌△BGF≌△CHG≌△DEH.
∴S正方形EFGH=S正方形ABCD﹣4S△AFE=16﹣4××1×3=10.
故答案为:10.
【点评】本题考查了正方形的性质、全等三角形的判定与性质以及三角形的面积公式,解题的关键是找出△AFE≌△BGF≌△CHG≌△DEH.本题属于中档题,难度不大,解决该题型题目时,利用分割图形求面积法求出面积是关键.
17.3π.
【解析】
试题分析:∵在四边形ABCD中,∠ABC=90°,BC=6,∠BAC=30°,∴AC=12,AB==6,S△ABC=×6×6=18,∴S扇形BAB′=π×6()2=9π,∴S1=18﹣9π.∵S△AB′C′=S△ABC=18,S扇形CAC′=π×122=12π,∴S2=12π﹣18,∴S阴影=S1+S2=18﹣9π+12π﹣18=3π.故答案为:3π.
考点:①扇形面积的计算;②旋转的性质.
18.504
【解析】
试题分析:,,根据题意可得:,当n+1为4的倍数时,则=.2016÷4=504.
考点:规律题
19.-1≤x<3
【解析】
试题分析:先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集.
试题解析:
由①得2x+5≤3x+6,即x≥-1;
由②得3(x-1)<2x,3x-3<2x,即x<3;
由以上可得-1≤x<3.
考点:一元一次不等式解集
20.30元
【解析】
试题分析:设第一批盒装花的进价是x元/盒,则第一批进的数量是:,第二批进的数量是:,再根据等量关系:第二批进的数量=第一批进的数量×2可得方程.
解:设第一批盒装花的进价是x元/盒,则
2×=,
解得
x=30
经检验,x=30是原方程的根.
答:第一批盒装花每盒的进价是30元.
考点:分式方程的应用.
21.(1)(2)不公平
【解析】
试题分析:(1)由把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,直接利用概率公式求解即可求得答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲胜,乙胜的情况,即可求得求概率,比较大小,即可知这个游戏是否公平.
解:(1)由于三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,
故从袋中随机摸出一球,标号是1的概率为:;
(2)这个游戏不公平.
画树状图得:
∵共有9种等可能的结果,两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=,P(乙胜)=.
∴P(甲胜)≠P(乙胜),
故这个游戏不公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
22.(1)见解析(2)20
【解析】
试题分析:(1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,∵OE=10.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴=,
∴BC=2OE=20,即BC的长是20.
【点评】本题考查了切线的判定与性质.解答(2)题时,也可以根据三角形中位线定理来求线段BC的长度.
23.(1)y=;(2)点C在双曲线上;理由见解析.
【解析】
试题分析:(1)∵AB∥x轴,∴∠ABO=∠BOD,∵∠ABO=∠CBD,∴∠BOD=∠OBD,∵OB=BD,∴∠BOD=∠BDO,∴△BOD是等边三角形,∴∠BOD=60°,∴B(1,);∵双曲线y=经过点B,∴k=1×=.∴双曲线的解析式为y=.
(2)∵∠ABO=60°,∠AOB=90°,∴∠A=30°,∴AB=2OB,∵AB=BC,∴BC=2OB,∴OC=OB,∴C(﹣1,﹣),∵﹣1×(﹣)=,∴点C在双曲线上.
考点:①反比例函数图象上点的坐标特征;②坐标与图形变化-旋转.
24.(1)证明见解析;(2)四边形AGBD是矩形.证明见解析.
【解析】
试题分析:(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;
(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=AB,CF=CD.
∴AE=CF.
在△AED和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴ 四边形AGBD是矩形.
考点:1.全等三角形的判定;2.平行四边形的性质;3.菱形的性质;4.矩形的判定.
25.(1);(2)①;②.
【解析】
试题分析:(1)∵直线y=x+4经过A,C两点,∴A点坐标是(﹣4,0),点C坐标是(0,4),又∵抛物线过A,C两点,∴,解得:,∴抛物线的解析式为.
(2)①如图1∵,∴抛物线的对称轴是直线x=﹣1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,∴PQ∥AO,PQ=AO=4.∵P,Q都在抛物线上,∴P,Q关于直线x=﹣1对称,∴P点的横坐标是﹣3,∴当x=﹣3时,,∴P点的坐标是;
②过P点作PF∥OC交AC于点F,∵PF∥OC,∴△PEF∽△OEC,∴.又∵,∴,设点F(x,x+4),∴,化简得:x2+4x+3=0,解得:x1=﹣1,x2=﹣3.当x=﹣1时,;当x=﹣3时,,即P点坐标是或.又∵点P在直线y=kx上,∴.
考点:二次函数综合题.
第I卷(选择题)
评卷人
得分
一、选择题(题型注释)
1.若|a|=5,b=﹣3,则a﹣b=(
)
A.2或8
B.﹣2或8
C.2或﹣8
D.﹣2或﹣8
2.函数y=自变量x的取值范围为(
)
A.x>﹣1
B.x<﹣1
C.x≠﹣1
D.x≠0
3.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于(
)
A.35°
B.45°
C.55°
D.65°4.下列说法中,不正确的是(
)
A.如果a、b互为相反数,则a+b=0
B.a为任意有理数,则它的倒数为
C.的系数是
D.的算术平方根是3
5.若m、n(n<m)是关于x的一元二次方程1﹣(x﹣a)(x﹣b)=0的两个根,且b<a,则m,n,b,a的大小关系是(
)
A.m<a<b<n
B.a<m<n<b
C.b<n<m<a
D.n<b<a<m
6.将如图所示表面带有图案的正方体沿某些棱展开后,得到的图形是(
)
A.
B.
C.
D.
7.若代数式2y2+3y+7的值为8,那么4y2+6y﹣9的值为(
)
A.2
B.﹣17
C.﹣7
D.7
8.a,b是有理数,它们在数轴上的对应点的位置如图所示,把a,﹣a,b,﹣b按照从小到大的顺序排列(
)
A.﹣b<﹣a<a<b
B.﹣a<﹣b<a<b
C.﹣b<a<﹣a<b
D.﹣b<b<﹣a<a
9.已知一组数据:1,2,6,3,3,下列说法正确的是(
)
A.众数是3
B.中位数是6
C.平均数是4
D.方差是5
10.如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为(
)
A.12
B.13
C.14
D.15
11.在同一平面直角坐标系中,函数y=mx+m与y=(m≠0)的图象可能是(
)
A.
B.
C.
D.
12.如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为(
)
A.
B.
C.
D.
第II卷(非选择题)
评卷人
得分
二、填空题(题型注释)
13.到2016年3月31日止,中外游客到凤凰古城旅游的人数累计到达130000000人;请你把130000000用科学记数法表示为
.
14.2﹣的绝对值是
.
15.分解因式:2x2﹣4x+2=
.
16.如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为
.
17.如图,在四边形ABCD中,∠ABC=90°,BC=6,将四边形ABCD绕点A逆时针旋转30°至四边形AB′C′D′处,则旋转过程中,边BC所扫过的区域(图中阴影部分)的面积为__________.
18.如图,在平面直角坐标系中,一个点从A(a1,a2)出发沿图中路线依次经过B(a3,a4),C(a5,a6),D(a7,a8),…,按此一直运动下去,则a2015+a2016的值为
.
评卷人
得分
三、解答题(题型注释)
19.解不等式组:
20.(2015 安顺)“母亲节”前夕,某商店根据市场调查,用3000元购进第一批盒装花,上市后很快售完,接着又用5000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花盒数的2倍,且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价是多少元?
21.甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
22.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线;
(2)当OE=10时,求BC的长.
23.如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.24.已知:如图,在平行四边形ABCD
中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形
BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
25.在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
参考答案
1.B
【解析】
试题分析:首先由绝对值的性质,求得a的值,然后利用有理数的减法法则计算即可.
解:∵|a|=5,
∴a=±5.
当a=5时,a﹣b=5﹣(﹣3)=5+3=8;
当=﹣5时,a﹣b=﹣5﹣(﹣3)=﹣5+3=﹣2.
故选:B.
【点评】本题主要考查的是绝对值的性质和有理数的减法法则的应用,掌握有理数的减法法则是解题的关键.
2.C
【解析】
试题分析:根据分式有意义的条件,分母不为0,得出x的取值范围即可.
解:∵x+1≠0,
∴x≠﹣1,
∴函数y=自变量x的取值范围为x≠﹣1,
故选C.
【点评】本题考查了函数自变量的取值范围问题,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
3.C
【解析】
试题分析:由已知条件和观察图形,利用对顶角相等、角平分线的性质和垂直的定义,再结合平角为180度,就可求出角的度数.
解:∵∠B0C=∠AOD=70°,
又∵OE平分∠BOC,
∴∠BOE=∠BOC=35°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠AOF=180°﹣∠EOF﹣∠BOE=55°.故选C.
点评:本题利用垂直的定义,对顶角和角平分线的性质计算,要注意领会由垂直得直角这一要点.
4.B
【解析】
试题分析:应用排除法逐项分析即可.
解:A:根据有理数的加法法则:如果两个数互为相反数,那么它们的和为0,故选项A正确;
B:如果a为0,则它的倒数没有意义,故选项B错误;
C:单项式中的数字因数叫做单项式的系数,而π是数而不是字母,故是系数,即选项C正确;
D:因为,而9的算术平方根是3,故选项D正确;
故:选B
点评:本题考查了算术平方根、相反数、倒数、单项式,解题的关键是概念要清楚.
5.D.
【解析】
试题分析:如图抛物线y=(x﹣a)(x﹣b)与x轴交于点(a,0),(b,0),抛物线与直线y=1的交点为(n,1),(m,1),由图象可知,n<b<a<m.故选D.
考点:抛物线与x轴的交点.
6.C.
【解析】
试题分析:由原正方体知,带图案的三个面相交于一点,而通过折叠后A、B都不符合,且D折叠后图的位置正好相反,所以能得到的图形是C.故选C.
考点:几何体的展开图.
7.C
【解析】解:∵2y2+3y+7的值为8,
∴2y2+3y+7=8,
∴2y2+3y=1,
∴2(2y2+3y)=2=4y2+6y,
把4y2+6y=2代入4y2+6y﹣9得:
4y2+6y﹣9=2﹣9=﹣7.
故选C.
【点评】代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取代数式4y2+6y的值,然后利用“整体代入法”求代数式的值.8.C
【解析】
试题分析:利用有理数大小的比较方法可得﹣a<b,﹣b<a,b>0>a进而求解.
解:观察数轴可知:b>0>a,且b的绝对值大于a的绝对值.
在b和﹣a两个正数中,﹣a<b;在a和﹣b两个负数中,绝对值大的反而小,则﹣b<a.
因此,﹣b<a<﹣a<b.
故选:C.
【点评】有理数大小的比较方法:正数大于0;负数小于0;正数大于一切负数;两个负数,绝对值大的反而小.
9.A
【解析】
试题分析:利用众数、算术平均数、中位数及方差的定义分别求解后即可确定正确的选项.
解:A、数据3出现2次,最多,故众数为3,故A选项正确;
B、排序后位于中间位置的数为3,故中位数为3,故B选项错误;
C、平均数为3,故C选项错误;
D、方差为2.8,故D选项错误.
故选:A.点评:本题考查了众数、算术平均数、中位数及方差的定义,属于基础题,比较简单.
10.C
【解析】
试题分析:如图,首先证明EF=6,继而得到DE=7;证明DE为△ABC的中位线,即可解决问题.
解:如图,∵∠AFC=90°,AE=CE,
∴EF==6,DE=1+6=7;
∵D,E分别是AB,AC的中点,
∴DE为△ABC的中位线,
∴BC=2DE=14,
故选C.
【点评】该题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题;牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键.
11.A
【解析】
试题分析:A、由函数y=mx+m的图象可知m>0,由函数y=的图象可知m>0,故A选项正确;
B、由函数y=mx+m的图象可知m<0,由函数y=的图象可知m>0,相矛盾,故B选项错误;
C、由函数y=mx+m的图象y随x的增大而减小,则m<0,而该直线与y轴交于正半轴,则m>0,相矛盾,故C选项错误;
D、由函数y=mx+m的图象y随x的增大而增大,则m>0,而该直线与y轴交于负半轴,则m<0,相矛盾,故D选项错误;
故选:A.
考点:反比例函数的图象;一次函数的图象
12.D.
【解析】
试题分析:如图,连接BF,已知BC=6,点E为BC的中点,可得BE=3,根据勾股定理求得AE=5,根据三角形的面积公式求出BH=,即可得BF=,因FE=BE=EC,可得∠BFC=90°,再由勾股定理可得CF=.
故答案选D.
考点:翻折变换;矩形的性质;勾股定理.13.1.3×108.
【解析】
试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
解:将13000
0000用科学记数法表示为1.3×108.
故答案为:1.3×108.
【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
14.﹣2.
【解析】
试题分析:先判断2﹣的正负值,再根据“正数的绝对值是它本身,负数的绝对值是其相反数”即可求解.
解:2﹣的绝对值是|2﹣|=﹣2.
故本题的答案﹣2.
点评:此题考查了绝对值的性质,要求掌握绝对值的性质及其定义,并能熟练运用到实际当中.
15.2(x﹣1)2.
【解析】
试题分析:先提取公因数2,再利用完全平方公式进行二次分解.完全平方公式:(a±b)2=a2±2ab+b2.
解:2x2﹣4x+2,
=2(x2﹣2x+1),
=2(x﹣1)2.
点评:本题主要考查提公因式法分解因式和利用完全平方公式分解因式,难点在于需要进行二次分解因式.
16.10
【解析】
试题分析:根据正方形的性质找出相等的边角关系,从而证出△AFE≌△BGF≌△CHG≌△DEH,再由正方形ABCD的面积为16,AE=1,找出AF的长度,根据S正方形EFGH=S正方形ABCD﹣4S△AFE即可得出结论.
解:∵四边形ABCD、EFGH均为正方形,
∴∠A=∠B=90°,∠EFG=90°,EF=FG.
∵∠AFE+∠BFG=90°,∠BFG+∠BGF=90°,
∴∠AFE=∠BGF.
在△AFE和△BGF中,,
∴△AFE≌△BGF(AAS),
∴BF=AE=1.
∵正方形ABCD的面积为16,
∴AB=4,AF=AB﹣BF=3.
同理可证出△AFE≌△BGF≌△CHG≌△DEH.
∴S正方形EFGH=S正方形ABCD﹣4S△AFE=16﹣4××1×3=10.
故答案为:10.
【点评】本题考查了正方形的性质、全等三角形的判定与性质以及三角形的面积公式,解题的关键是找出△AFE≌△BGF≌△CHG≌△DEH.本题属于中档题,难度不大,解决该题型题目时,利用分割图形求面积法求出面积是关键.
17.3π.
【解析】
试题分析:∵在四边形ABCD中,∠ABC=90°,BC=6,∠BAC=30°,∴AC=12,AB==6,S△ABC=×6×6=18,∴S扇形BAB′=π×6()2=9π,∴S1=18﹣9π.∵S△AB′C′=S△ABC=18,S扇形CAC′=π×122=12π,∴S2=12π﹣18,∴S阴影=S1+S2=18﹣9π+12π﹣18=3π.故答案为:3π.
考点:①扇形面积的计算;②旋转的性质.
18.504
【解析】
试题分析:,,根据题意可得:,当n+1为4的倍数时,则=.2016÷4=504.
考点:规律题
19.-1≤x<3
【解析】
试题分析:先解不等式组中的每一个不等式的解集,再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集.
试题解析:
由①得2x+5≤3x+6,即x≥-1;
由②得3(x-1)<2x,3x-3<2x,即x<3;
由以上可得-1≤x<3.
考点:一元一次不等式解集
20.30元
【解析】
试题分析:设第一批盒装花的进价是x元/盒,则第一批进的数量是:,第二批进的数量是:,再根据等量关系:第二批进的数量=第一批进的数量×2可得方程.
解:设第一批盒装花的进价是x元/盒,则
2×=,
解得
x=30
经检验,x=30是原方程的根.
答:第一批盒装花每盒的进价是30元.
考点:分式方程的应用.
21.(1)(2)不公平
【解析】
试题分析:(1)由把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,直接利用概率公式求解即可求得答案;(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与甲胜,乙胜的情况,即可求得求概率,比较大小,即可知这个游戏是否公平.
解:(1)由于三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中,
故从袋中随机摸出一球,标号是1的概率为:;
(2)这个游戏不公平.
画树状图得:
∵共有9种等可能的结果,两次摸出的球的标号之和为偶数的有5种情况,两次摸出的球的标号之和为奇数的有4种情况,
∴P(甲胜)=,P(乙胜)=.
∴P(甲胜)≠P(乙胜),
故这个游戏不公平.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.
22.(1)见解析(2)20
【解析】
试题分析:(1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,∵OE=10.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴=,
∴BC=2OE=20,即BC的长是20.
【点评】本题考查了切线的判定与性质.解答(2)题时,也可以根据三角形中位线定理来求线段BC的长度.
23.(1)y=;(2)点C在双曲线上;理由见解析.
【解析】
试题分析:(1)∵AB∥x轴,∴∠ABO=∠BOD,∵∠ABO=∠CBD,∴∠BOD=∠OBD,∵OB=BD,∴∠BOD=∠BDO,∴△BOD是等边三角形,∴∠BOD=60°,∴B(1,);∵双曲线y=经过点B,∴k=1×=.∴双曲线的解析式为y=.
(2)∵∠ABO=60°,∠AOB=90°,∴∠A=30°,∴AB=2OB,∵AB=BC,∴BC=2OB,∴OC=OB,∴C(﹣1,﹣),∵﹣1×(﹣)=,∴点C在双曲线上.
考点:①反比例函数图象上点的坐标特征;②坐标与图形变化-旋转.
24.(1)证明见解析;(2)四边形AGBD是矩形.证明见解析.
【解析】
试题分析:(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS,ASA,SSS)来证明全等;
(2)先由菱形的性质得出AE=BE=DE,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD是矩形.
试题解析:(1)∵四边形ABCD是平行四边形,
∴∠4=∠C,AD=CB,AB=CD.
∵点E、F分别是AB、CD的中点,
∴AE=AB,CF=CD.
∴AE=CF.
在△AED和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)当四边形BEDF是菱形时,四边形AGBD是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵AG∥BD,
∴四边形AGBD是平行四边形.
∵四边形BEDF是菱形,
∴DE=BE.
∵AE=BE,
∴AE=BE=DE.
∴∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°.
即∠ADB=90°.
∴ 四边形AGBD是矩形.
考点:1.全等三角形的判定;2.平行四边形的性质;3.菱形的性质;4.矩形的判定.
25.(1);(2)①;②.
【解析】
试题分析:(1)∵直线y=x+4经过A,C两点,∴A点坐标是(﹣4,0),点C坐标是(0,4),又∵抛物线过A,C两点,∴,解得:,∴抛物线的解析式为.
(2)①如图1∵,∴抛物线的对称轴是直线x=﹣1.
∵以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,∴PQ∥AO,PQ=AO=4.∵P,Q都在抛物线上,∴P,Q关于直线x=﹣1对称,∴P点的横坐标是﹣3,∴当x=﹣3时,,∴P点的坐标是;
②过P点作PF∥OC交AC于点F,∵PF∥OC,∴△PEF∽△OEC,∴.又∵,∴,设点F(x,x+4),∴,化简得:x2+4x+3=0,解得:x1=﹣1,x2=﹣3.当x=﹣1时,;当x=﹣3时,,即P点坐标是或.又∵点P在直线y=kx上,∴.
考点:二次函数综合题.
同课章节目录
