1.5定积分的概念1
图片预览




文档简介
课件17张PPT。1.5 定积分的概念1.5.1 曲边梯形的面积牛顿
英国著名的物理学家、数学家和天文学家,是十七世纪最伟大的科学巨匠。
牛顿在前人工作的基础上建立了二项式定理。并和莱布尼茨几乎同时创立微积分学,得出了导数、积分的概念和运算法则,阐明了求导数和求积分是互逆的两种运算。 莱布尼兹
17、18世纪之交德国最重要的数学家、物理学家和哲学家,一个举世罕见的科学天才,和牛顿同为微积分的创建人。他博览群书,涉猎百科,对丰富人类的科学知识宝库做出了不可磨灭的贡献。1.连续函数:
一般地,如果函数y=f(x)在某个区间I上的图象是一条连续不断的曲线,那么我们就把它称为区间I上的连续函数.2.曲边梯形:
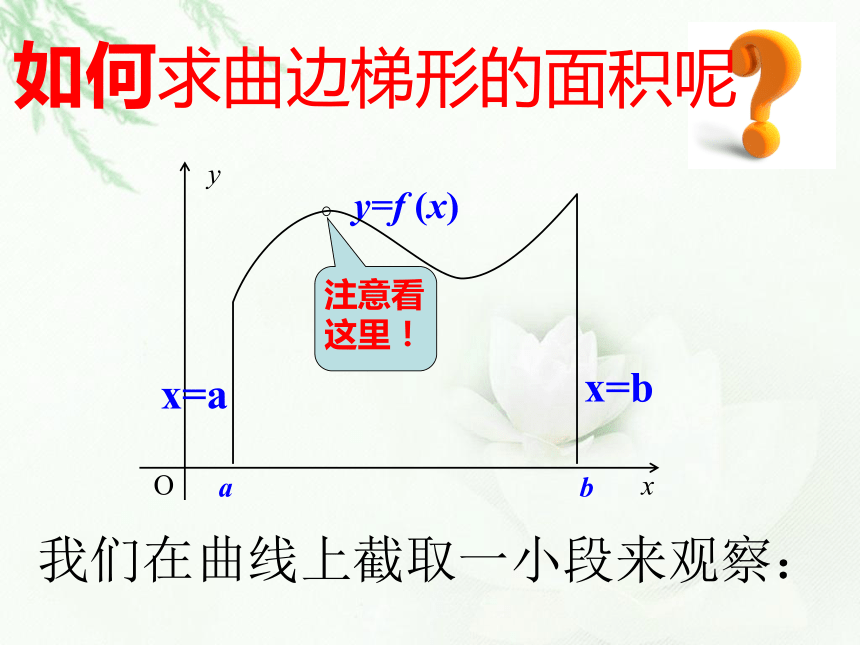
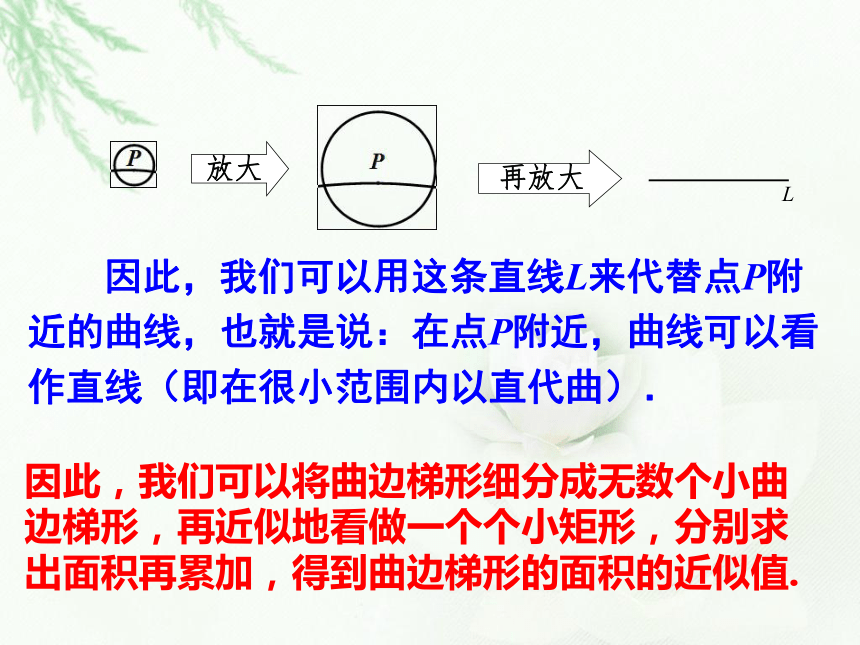
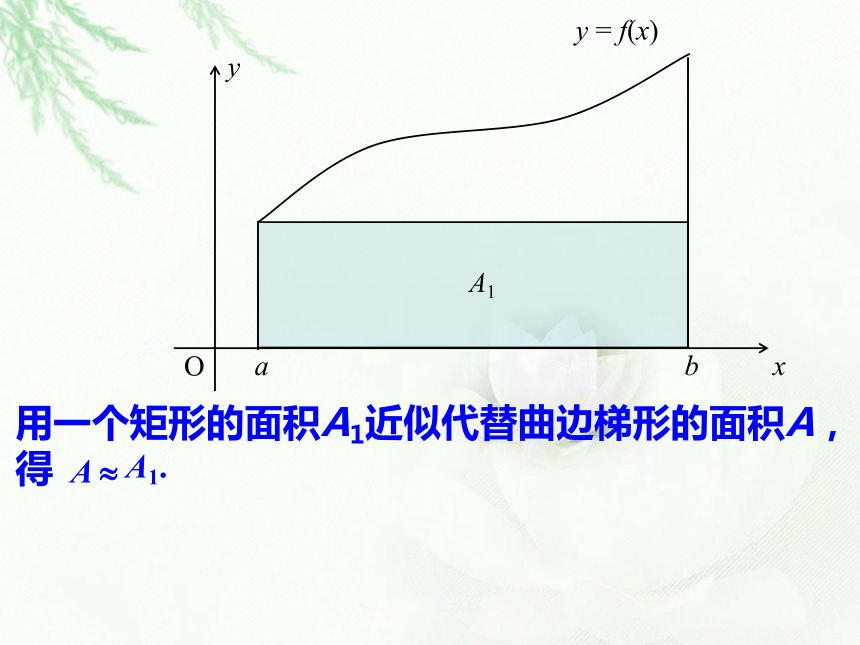
在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形。如何求曲边梯形的面积呢我们在曲线上截取一小段来观察:注意看这里! 因此,我们可以用这条直线L来代替点P附近的曲线,也就是说:在点P附近,曲线可以看作直线(即在很小范围内以直代曲).放大再放大因此,我们可以将曲边梯形细分成无数个小曲边梯形,再近似地看做一个个小矩形,分别求出面积再累加,得到曲边梯形的面积的近似值. y = f(x)用一个矩形的面积A1近似代替曲边梯形的面积A,
得用两个矩形的面积 近似代替曲边梯形
的面积A,得A ? A1+ A2+ A3+ A4用四个矩形的面积 近似代替曲边梯形
的面积A, 得A ? A1+ A2 + ? ? ? + An 将曲边梯形分成 n个小曲边梯形,并用小矩形的面积代替小曲边梯形的面积, 于是曲边梯形的面积A近似为—— 以直代曲,无限逼近 演示(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作例1.求抛物线y=x2、直线x=1和x轴所围成的
曲边梯形的面积。(2) 近似代替当n很大,即△x很小时,在第i个区间上用区间左端点处的函数值代替小曲边梯形的高,从图形看,就是用平行于x轴的直线段近似地代替小区别梯形的曲边,用小矩形的面积近似地代替相应小曲边梯形的面积,则有: 用右端点处的函数值代替小曲边梯形的高行吗?用区间内任意一点处的函数值代替行吗?为什么?(3)求和
图中小矩形面积之和为:(4)取极限
曲边梯形的面积S是当n趋向于无穷大时,小矩形面积之和的极限:小结:求由连续曲线y=f(x)对应的曲边梯形面积的方法(1)分割 (2)近似代替 (4)取极限(3)求和BD自主检测:CC巩固提高:
课本第42业练习提示:
英国著名的物理学家、数学家和天文学家,是十七世纪最伟大的科学巨匠。
牛顿在前人工作的基础上建立了二项式定理。并和莱布尼茨几乎同时创立微积分学,得出了导数、积分的概念和运算法则,阐明了求导数和求积分是互逆的两种运算。 莱布尼兹
17、18世纪之交德国最重要的数学家、物理学家和哲学家,一个举世罕见的科学天才,和牛顿同为微积分的创建人。他博览群书,涉猎百科,对丰富人类的科学知识宝库做出了不可磨灭的贡献。1.连续函数:
一般地,如果函数y=f(x)在某个区间I上的图象是一条连续不断的曲线,那么我们就把它称为区间I上的连续函数.2.曲边梯形:
在直角坐标系中,由连续曲线y=f(x),直线x=a、x=b及x轴所围成的图形叫做曲边梯形。如何求曲边梯形的面积呢我们在曲线上截取一小段来观察:注意看这里! 因此,我们可以用这条直线L来代替点P附近的曲线,也就是说:在点P附近,曲线可以看作直线(即在很小范围内以直代曲).放大再放大因此,我们可以将曲边梯形细分成无数个小曲边梯形,再近似地看做一个个小矩形,分别求出面积再累加,得到曲边梯形的面积的近似值. y = f(x)用一个矩形的面积A1近似代替曲边梯形的面积A,
得用两个矩形的面积 近似代替曲边梯形
的面积A,得A ? A1+ A2+ A3+ A4用四个矩形的面积 近似代替曲边梯形
的面积A, 得A ? A1+ A2 + ? ? ? + An 将曲边梯形分成 n个小曲边梯形,并用小矩形的面积代替小曲边梯形的面积, 于是曲边梯形的面积A近似为—— 以直代曲,无限逼近 演示(1)分割把区间[0,1]等分成n个小区间:过各区间端点作x轴的垂线,从而得到n个小曲边梯形,他们的面积分别记作例1.求抛物线y=x2、直线x=1和x轴所围成的
曲边梯形的面积。(2) 近似代替当n很大,即△x很小时,在第i个区间上用区间左端点处的函数值代替小曲边梯形的高,从图形看,就是用平行于x轴的直线段近似地代替小区别梯形的曲边,用小矩形的面积近似地代替相应小曲边梯形的面积,则有: 用右端点处的函数值代替小曲边梯形的高行吗?用区间内任意一点处的函数值代替行吗?为什么?(3)求和
图中小矩形面积之和为:(4)取极限
曲边梯形的面积S是当n趋向于无穷大时,小矩形面积之和的极限:小结:求由连续曲线y=f(x)对应的曲边梯形面积的方法(1)分割 (2)近似代替 (4)取极限(3)求和BD自主检测:CC巩固提高:
课本第42业练习提示:
