21.3 二次函数与一元二次方程课件(第1课时)
文档属性
| 名称 | 21.3 二次函数与一元二次方程课件(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 788.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-23 16:10:42 | ||
图片预览







文档简介
课件23张PPT。21.3 二次函数与一元二次方程导入新课讲授新课当堂练习课堂小结第1课时 二次函数与一元二次方程1.通过探索,理解二次函数与一元二次方程之间的联系;
(重点)
2.会用二次函数图象求一元二次方程的近似解; (重点)
3.通过研究二次函数与一元二次方程的联系体会数形结合思想
的应用.(难点)温故知新(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根 -2 0-22 02 我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.
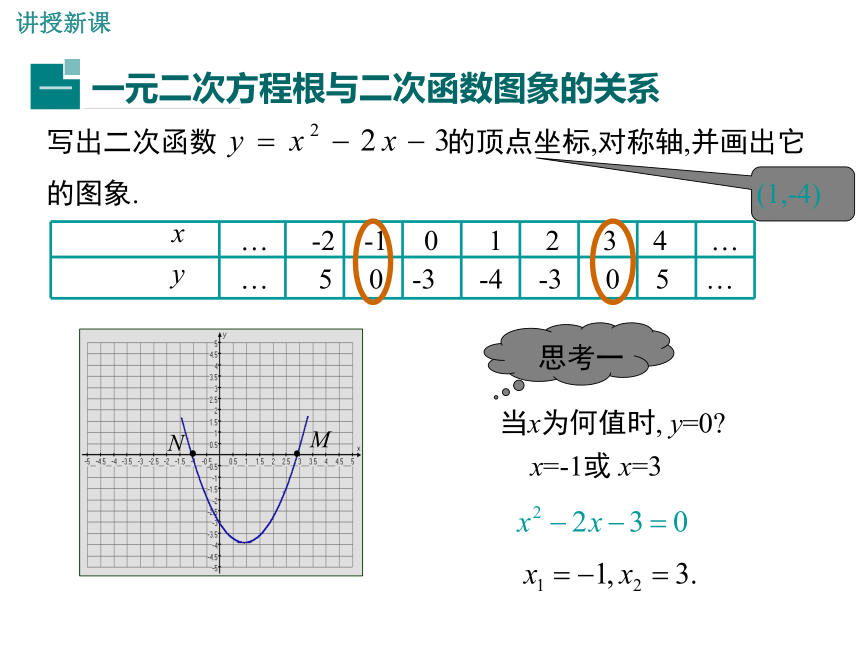
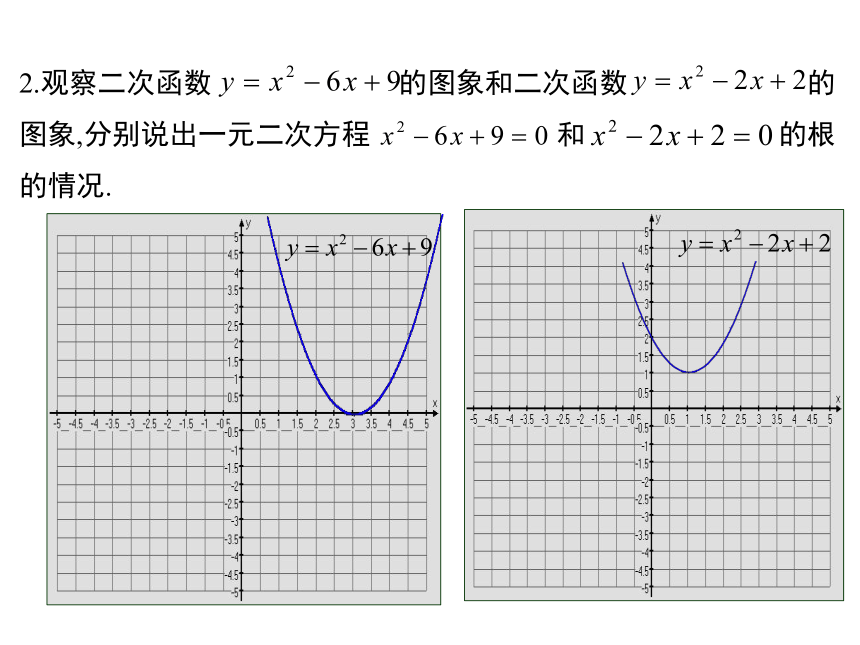
问题:现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢?导入新课回顾与思考xy… -2 -1 0 1 2 3 4 …… 5 0 -3 -4 -3 0 5 …NM当x为何值时, y=0?写出二次函数 的顶点坐标,对称轴,并画出它的图象.x=-1或 x=3讲授新课一般地,如果二次函数 的图象与x轴有两个交点( ,0)、( ,0 )那么一元二次方程 有两个不相等的实数根 、 ,反之亦成立. 1. 不画图象,你能说出函数 的图象与 x 轴的交点坐标吗?解:当y=0时,所以,函数 的图象与 x 轴的交点坐标为(-3,0)和(2,0).解得2.观察二次函数 的图象和二次函数 的图象,分别说出一元二次方程 和 的根的情况.例:求一元二次方程 的根的近似值(精确到0.1). 分析:一元二次方程 x2-2x-1=0 的根就是抛物线 y=x2-2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.解:画出函数 y=x2-2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.
同理可得另一近似值为x2≈2.4.一元二次方程的图象解法利用二次函数的图象求一元二次方程2x2+x-15=0的近似根.(1)用描点法作二次函数 y=2x2+x-15的图象;(2)观察估计二次函数 y=2x2+x-15的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个是-3,另一个在2与3之间,分别约为-3和2.5(可将单位长再十等分,借助计算器确定其近似值);(3)确定方程2x2+x-15=0的解;由此可知,方程2x2+x-15=0的近似根为:x1≈-3,x2≈2.5. 一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 . 既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.例: 如图,丁丁在扔铅球时,铅球沿抛物线 运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.(1)当铅球离地面的高度为2.1m它离初始位置的水平
距离是多少?(2)铅球离地面的高度能否达到2.5m,它离初始位置
的水平距离是多少?(3)铅球离地面的高度能否达到3m?为什么?xy典例精析解:(1)由抛物线的表达式得:即 x2-6x+5=0解得 x1=1,x2=5当铅球离地面高度为2.1m时,它离初始位置的水平距离是1m或5m;当铅球离地面高度为2.5m时,它离初始位置的水平距离是3m;(2)由抛物线的表达式得:即 x2-6x+9=0解得 x1=x2=3所以铅球离地面高度不能达到3m.(3)由抛物线的表达式得:即 x2-6x+14=0因为Δ =(-6)2-4×14<0,所以方程无实数根, 从例题可以看出,已知二次函数 y=ax2+bx+c(a ≠ 0)某一个函数值y=m求对应的自变量的值时,需要解一元二次方程ax2+bx+c=m,这样二次函数与一元二次方程就紧密地联系起来了.1.求下列抛物线与x轴的交点的横坐标:它与x轴有交点,则y=0解这个方程 (x-2)(x+1)= 0∴ x1=2, x2=-1∴抛物线与x轴交点的横坐标分别为2,-1.解:当堂练习它与x轴有交点,则 y=0∴ x1= x2=∴ 与x轴交点的横坐标为 .解:解:Δ =(-2)2-4×1×3<0此方程无解,所以,抛物线 y=x2-2x+3与x轴没有交点.a=1 , b=-2 , c=3(3) y=x2-2x+3x2-2x+3=02.用图象法求一元二次方程 的解的近似值
(精确到0.1). 解:画出x2+x-1=0的图象,如图所示,由图象知,方程由两个根,一个在-2和-1之间,另一个在0到1之间.通过估算,可得到抛物线与x轴交点的横坐标大约为-1.6和0.6.即一元二次方程的实数根为x1≈-1.6,x2≈0.6. 二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系.有两个交点有两个不相等的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0课堂小结见《学练优》本课时练习课后作业
(重点)
2.会用二次函数图象求一元二次方程的近似解; (重点)
3.通过研究二次函数与一元二次方程的联系体会数形结合思想
的应用.(难点)温故知新(1)一次函数y=x+2的图象与x轴的交点为( , )
一元一次方程x+2=0的根为________
(2) 一次函数y=-3x+6的图象与x轴的交点为( , )
一元一次方程-3x+6=0的根为________
思考:一次函数y=kx+b的图象与x轴的交点与一元一次方程kx+b=0的根有什么关系?
一次函数y=kx+b的图象与x轴的交点的横坐标就是一元一次方程kx+b=0的根 -2 0-22 02 我们学习了一元一次方程kx+b=0(k≠0)和一次函数y=kx+b(k≠0)后,讨论了它们之间的关系.当一次函数中的函数值y=0时,一次函数y=kx+b就转化成了一元一次方程kx+b=0且一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解.
问题:现在我们学习了一元二次方程ax2+bx+c=0(a≠0)和二次函数y=ax2+bx+c(a≠0),它们之间是否也存在一定的关系呢?导入新课回顾与思考xy… -2 -1 0 1 2 3 4 …… 5 0 -3 -4 -3 0 5 …NM当x为何值时, y=0?写出二次函数 的顶点坐标,对称轴,并画出它的图象.x=-1或 x=3讲授新课一般地,如果二次函数 的图象与x轴有两个交点( ,0)、( ,0 )那么一元二次方程 有两个不相等的实数根 、 ,反之亦成立. 1. 不画图象,你能说出函数 的图象与 x 轴的交点坐标吗?解:当y=0时,所以,函数 的图象与 x 轴的交点坐标为(-3,0)和(2,0).解得2.观察二次函数 的图象和二次函数 的图象,分别说出一元二次方程 和 的根的情况.例:求一元二次方程 的根的近似值(精确到0.1). 分析:一元二次方程 x2-2x-1=0 的根就是抛物线 y=x2-2x-1 与x轴的交点的横坐标,因此我们可以先画出这条抛物线,然后从图上找出它与x轴的交点的横坐标,这种解一元二次方程的方法叫作图象法.解:画出函数 y=x2-2x-1 的图象(如下图),由图象可知,方程有两个实数根,一个在-1与0之间,另一个在2与3之间.先求位于-1到0之间的根,由图象可估计这个根是-0.4或-0.5,利用计算器进行探索,见下表:观察上表可以发现,当x分别取-0.4和-0.5时,对应的y由负变正,可见在-0.5与-0.4之间肯定有一个x使y=0,即有y=x2-2x-1的一个根,题目只要求精确到0.1,这时取x=-0.4或x=-0.5都符合要求.但当x=-0.4时更为接近0.故x1≈-0.4.
同理可得另一近似值为x2≈2.4.一元二次方程的图象解法利用二次函数的图象求一元二次方程2x2+x-15=0的近似根.(1)用描点法作二次函数 y=2x2+x-15的图象;(2)观察估计二次函数 y=2x2+x-15的图象与x轴的交点的横坐标;由图象可知,图象与x轴有两个交点,其横坐标一个是-3,另一个在2与3之间,分别约为-3和2.5(可将单位长再十等分,借助计算器确定其近似值);(3)确定方程2x2+x-15=0的解;由此可知,方程2x2+x-15=0的近似根为:x1≈-3,x2≈2.5. 一元二次方程ax2+bx+c=m的根就是二次函数y=ax2+bx+c 与直线y=m(m是实数)图象交点的横坐标 . 既可以用求根公式求二次方程的根,也可以通过画二次函数图象来估计一元二次方程的根.例: 如图,丁丁在扔铅球时,铅球沿抛物线 运行,其中x是铅球离初始位置的水平距离,y是铅球离地面的高度.(1)当铅球离地面的高度为2.1m它离初始位置的水平
距离是多少?(2)铅球离地面的高度能否达到2.5m,它离初始位置
的水平距离是多少?(3)铅球离地面的高度能否达到3m?为什么?xy典例精析解:(1)由抛物线的表达式得:即 x2-6x+5=0解得 x1=1,x2=5当铅球离地面高度为2.1m时,它离初始位置的水平距离是1m或5m;当铅球离地面高度为2.5m时,它离初始位置的水平距离是3m;(2)由抛物线的表达式得:即 x2-6x+9=0解得 x1=x2=3所以铅球离地面高度不能达到3m.(3)由抛物线的表达式得:即 x2-6x+14=0因为Δ =(-6)2-4×14<0,所以方程无实数根, 从例题可以看出,已知二次函数 y=ax2+bx+c(a ≠ 0)某一个函数值y=m求对应的自变量的值时,需要解一元二次方程ax2+bx+c=m,这样二次函数与一元二次方程就紧密地联系起来了.1.求下列抛物线与x轴的交点的横坐标:它与x轴有交点,则y=0解这个方程 (x-2)(x+1)= 0∴ x1=2, x2=-1∴抛物线与x轴交点的横坐标分别为2,-1.解:当堂练习它与x轴有交点,则 y=0∴ x1= x2=∴ 与x轴交点的横坐标为 .解:解:Δ =(-2)2-4×1×3<0此方程无解,所以,抛物线 y=x2-2x+3与x轴没有交点.a=1 , b=-2 , c=3(3) y=x2-2x+3x2-2x+3=02.用图象法求一元二次方程 的解的近似值
(精确到0.1). 解:画出x2+x-1=0的图象,如图所示,由图象知,方程由两个根,一个在-2和-1之间,另一个在0到1之间.通过估算,可得到抛物线与x轴交点的横坐标大约为-1.6和0.6.即一元二次方程的实数根为x1≈-1.6,x2≈0.6. 二次函数y=ax2+bx+c的图象与x轴交点的坐标与一元二次方程ax2+bx+c=0根的关系.有两个交点有两个不相等的实数根b2-4ac > 0有一个交点有两个相等的实数根b2-4ac = 0没有交点没有实数根b2-4ac < 0课堂小结见《学练优》本课时练习课后作业
