21.3二次函数与一元二次不等式课件(第2课时)
文档属性
| 名称 | 21.3二次函数与一元二次不等式课件(第2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-23 16:15:02 | ||
图片预览





文档简介
课件12张PPT。21.3 二次函数与一元二次方程第2课时 二次函数与一元二次不等式问题1:上节课学到的一元二次方程ax2+bx+c=0(a≠0)的根和二次函数y=ax2+bx+c(a≠0)的图象,它们存在着怎样的联系?导入新课回顾与思考问题2:一次函数与一元一次不等式有怎样的联系?问题3:那你可以猜测到二次函数与一元二次不等式的联系吗?思考1:函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=0的根是 __________;
不等式ax2+bx+c>0的解集 是___________;
不等式ax2+bx+c<0的解集 是_________.
yx1=-1, x2=3x<-1或x>3-1(1) ①-x2+x+2=0;
②-x2+x+2>0;
③-x2+x+2<0.
(2) ①x2-4x+4=0;
②x2-4x+4>0;
③x2-4x+4<0.
(3) ①-x2+x-2=0;
②-x2+x-2>0;
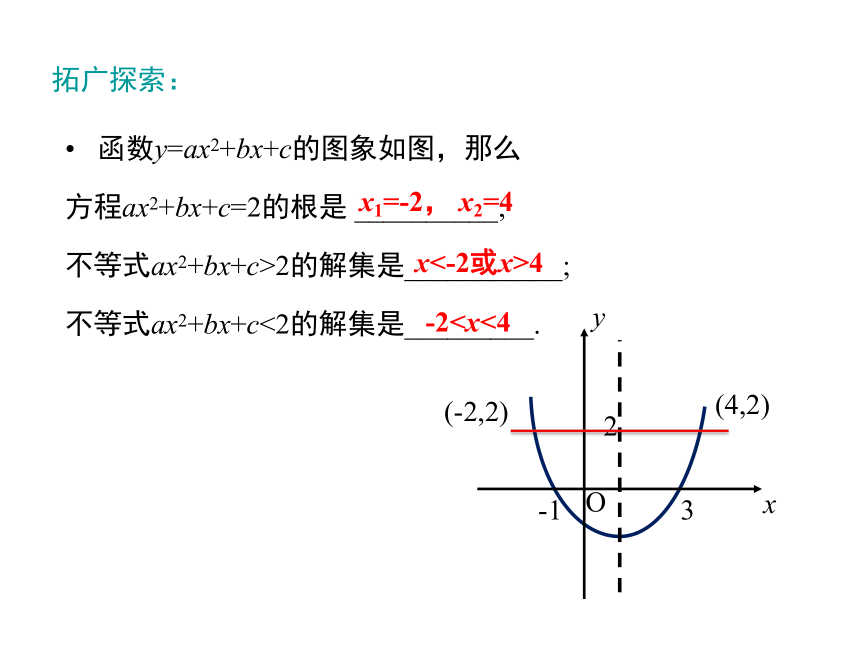
③-x2+x-2<0.x1=-1 , x2=21 < x<2x <-1 , x >2x2-4x+4=0 x1 =x2=2 x≠2的一切实数 x无解-x2+x-2=0 x无解 x无解 x为全体实数拓广探索:函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 __________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3-1Ox2(4,2)(-2,2)x1=-2, x2=4x<-2或x>4-20(a≠0)的解集是x≠2 的一切实数,那么函数y=ax2+bx+c的图象与 x轴有______ 个交点,坐标是________________.
方程ax2+bx+c=0的根是______________.
1(2,0)x=2思考3:如果方程ax2+bx+c=0 (a≠0)没有实数根,那么
函数y=ax2+bx+c的图象与 x轴有______个交点;
不等式ax2+bx+c<0的解集是多少?0解:(1)当a>0时, ax2+bx+c<0无解;(2)当a<0时, ax2+bx+c<0的解集是一切实数.1.(1)x取何值时,关于x的二次三项式 x2-3x+2的值为负数;
(2)a是什么实数时,不等式ax2+ax-1>0 无解?
当堂练习解:(1) 1<x<2;
(2)△=a2+4a<0,
解得-4≤a<0.
2.当1<x<3时,二次函数y=x2-(k+1)x+k的图象在x轴下侧,求k的取值范围.
解:y=x2-(k+1)x+k=(x-k)(x-1),与x轴交点坐标为(1,0)、(k,0).
因为当1<x<3时有y<0,所以k≥3.3.已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么? (2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?解:(1)该方程解为 x1=2,x2=4;
(2)当x<2,x>4时y>0;
(3)当2<x<4时y<0.x2x1xyoO△>0△=0△<0x1 ; x2x1 =x2
=-b/2a没有实数根xx2x ≠ x1的一切实数所有实数x1
方程ax2+bx+c=0的根是 __________;
不等式ax2+bx+c>0的解集 是___________;
不等式ax2+bx+c<0的解集 是_________.
yx1=-1, x2=3x<-1或x>3-1
②-x2+x+2>0;
③-x2+x+2<0.
(2) ①x2-4x+4=0;
②x2-4x+4>0;
③x2-4x+4<0.
(3) ①-x2+x-2=0;
②-x2+x-2>0;
③-x2+x-2<0.x1=-1 , x2=21 < x<2x <-1 , x >2x2-4x+4=0 x1 =x2=2 x≠2的一切实数 x无解-x2+x-2=0 x无解 x无解 x为全体实数拓广探索:函数y=ax2+bx+c的图象如图,那么
方程ax2+bx+c=2的根是 __________;
不等式ax2+bx+c>2的解集是___________;
不等式ax2+bx+c<2的解集是_________.
3-1Ox2(4,2)(-2,2)x1=-2, x2=4x<-2或x>4-2
方程ax2+bx+c=0的根是______________.
1(2,0)x=2思考3:如果方程ax2+bx+c=0 (a≠0)没有实数根,那么
函数y=ax2+bx+c的图象与 x轴有______个交点;
不等式ax2+bx+c<0的解集是多少?0解:(1)当a>0时, ax2+bx+c<0无解;(2)当a<0时, ax2+bx+c<0的解集是一切实数.1.(1)x取何值时,关于x的二次三项式 x2-3x+2的值为负数;
(2)a是什么实数时,不等式ax2+ax-1>0 无解?
当堂练习解:(1) 1<x<2;
(2)△=a2+4a<0,
解得-4≤a<0.
2.当1<x<3时,二次函数y=x2-(k+1)x+k的图象在x轴下侧,求k的取值范围.
解:y=x2-(k+1)x+k=(x-k)(x-1),与x轴交点坐标为(1,0)、(k,0).
因为当1<x<3时有y<0,所以k≥3.3.已知二次函数 的图象,利用图象回答问题:
(1)方程 的解是什么? (2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?解:(1)该方程解为 x1=2,x2=4;
(2)当x<2,x>4时y>0;
(3)当2<x<4时y<0.x2x1xyoO△>0△=0△<0x1 ; x2x1 =x2
=-b/2a没有实数根x
