第14章 勾股定理 达标检测卷
图片预览



文档简介
第14章达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.下列各组线段能构成直角三角形的一组是( )
A.30,40,50
B.7,12,13
C.5,9,12
D.3,4,6
2.用反证法证明“如果在△ABC中,∠C=90°,那么∠A,∠B中至少有一个角不大于45°”时,应先假设( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
(第3题)
3.如图,图中有一个正方形,此正方形的面积是( )
A.16
B.8
C.4
D.2
4.满足下列条件的△ABC不是直角三角形的是( )
A.∠A=∠B-∠C
B.∠A∶∠B∶∠C=1∶1∶2
C.b2=a2-c2
D.a∶b∶c=1∶1∶2
5.若△ABC的三边长分别为a,b,c,且满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
(第6题)
6.如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处朝张大爷的房子方向折断倒下,量得倒下部分的长是10米,大树倒下时会砸到张大爷的房子吗( )
A.一定不会
B.可能会
C.一定会
D.以上答案都不对
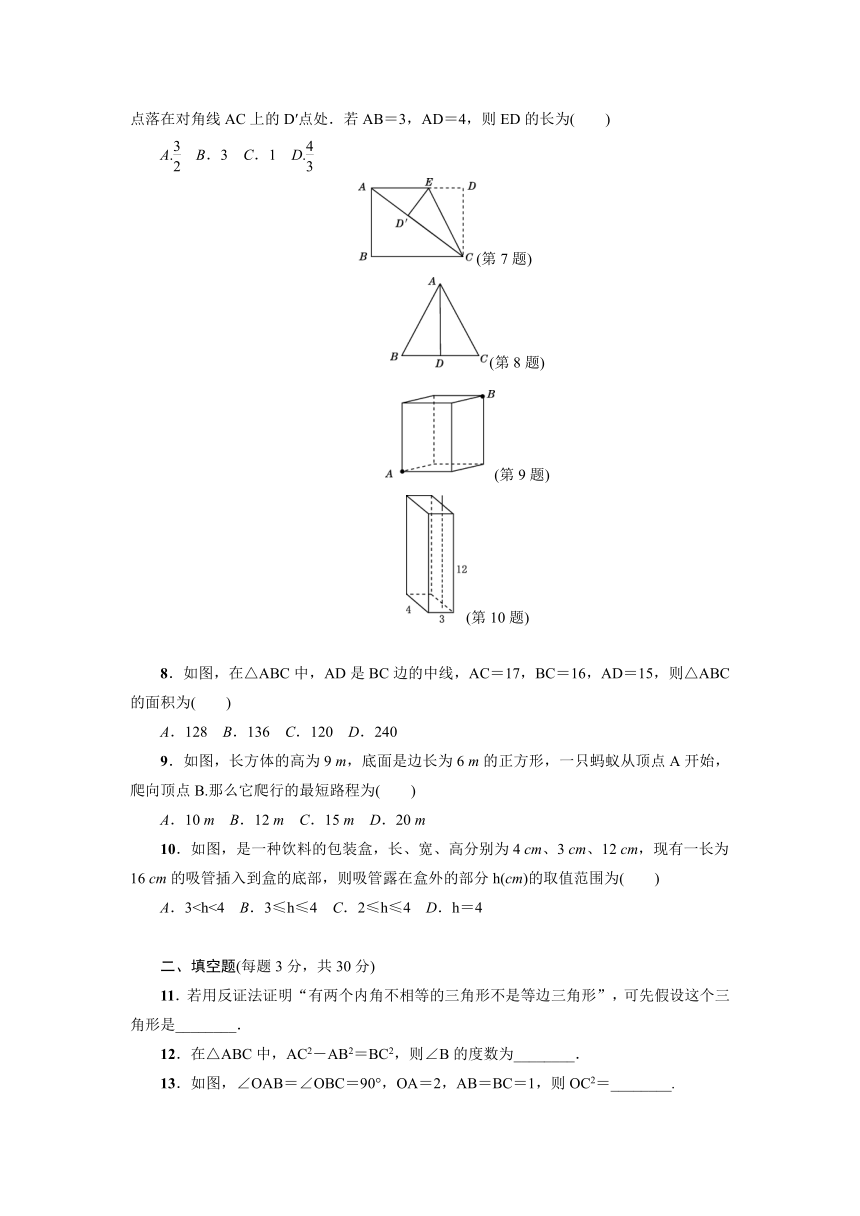
7.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线AC上的D′点处.若AB=3,AD=4,则ED的长为( )
A.
B.3
C.1
D.
(第7题)
(第8题)
(第9题)
(第10题)
8.如图,在△ABC中,AD是BC边的中线,AC=17,BC=16,AD=15,则△ABC的面积为( )
A.128
B.136
C.120
D.240
9.如图,长方体的高为9
m,底面是边长为6
m的正方形,一只蚂蚁从顶点A开始,爬向顶点B.那么它爬行的最短路程为( )
A.10
m
B.12
m
C.15
m
D.20
m
10.如图,是一种饮料的包装盒,长、宽、高分别为4
cm、3
cm、12
cm,现有一长为16
cm的吸管插入到盒的底部,则吸管露在盒外的部分h(cm)的取值范围为( )
A.3B.3≤h≤4
C.2≤h≤4
D.h=4
二、填空题(每题3分,共30分)
11.若用反证法证明“有两个内角不相等的三角形不是等边三角形”,可先假设这个三角形是________.
12.在△ABC中,AC2-AB2=BC2,则∠B的度数为________.
13.如图,∠OAB=∠OBC=90°,OA=2,AB=BC=1,则OC2=________.
(第13题)
(第14题)
(第19题)
(第20题)
14.如图,直角三角形三边上的半圆形面积从小到大依次记为S1、S2、S3,则S1、S2、S3之间的关系是________.
15.木工师傅要做一个长方形桌面,做好后量得长为80
cm,宽为60
cm,对角线长为100
cm,则这个桌面________(填“合格”或“不合格”).
16.若直角三角形的两边长分别为a、b,且满足(a-3)2+|b-4|=0,则该直角三角形的斜边长为________.
17.等腰三角形ABC的腰AB为10
cm,底边BC为16
cm,则面积为________cm2.
18.在△ABC中,AB=13
cm,AC=20
cm,BC边上的高为12
cm,则△ABC的面积为________.
19.《中华人民共和国道路管理条例》规定:小汽车在城市街道上的行驶速度不得超过70
km/h.如图,一辆小汽车在一条城市街道上直道行驶时,某一时刻刚好行驶到路对面车速检测仪观测点A正前方50
m的C处,过了6
s后,行驶到B处的小汽车与车速检测仪间的距离变为130
m,请你判断:这辆小汽车________(填“是”或“否”)超速了.
20.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;…,依照此方法继续作下去,得OP2
015=________.
三、解答题(21,22题每题8分,23,24题每题10分,25,26题每题12分,共60分)
21.用反证法证明一个三角形中不能有两个角是直角.
22.园丁住宅小区有一块草坪如图,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.
(第22题)
23.如图,将断落的电话线拉直,使其一端在电线杆顶端A处,另一端落在地面C处,这时测得BC=6米,再把电话线沿电线杆拉扯,使AD=AB,并量出电话线剩余部分(即CD)的长为2米,你能由此算出电线杆AB的高吗?
(第23题)
24.如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36
cm,点P从点A开始沿AB边向B点以每秒1
cm的速度移动;点Q从点B开始沿BC边向点C以每秒2
cm的速度移动,如果P,Q同时出发,问过3
s时,△BPQ的面积为多少?
(第24题)
25.如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有一学校,点A到公路MN的距离为80
m,现有一拖拉机在公路MN上以18
km/h的速度沿PN方向行驶,拖拉机行驶时周围100
m以内都会受到噪音的影响,试问该校受影响的时间为多长?
(第25题)
26.图甲是任意一个直角三角形ABC,它的两条直角边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为(a+b)的正方形内.
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③的四条边长都是________,且每个角都是直角,所以③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②的面积之和为________;
(4)图乙中①②的面积之和与图丙中③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
(第26题)
答案
一、1.A 2.A 3.B 4.D 5.D 6.A 7.A 8.C 9.C 10.B
二、11.等边三角形 12.90° 13.6
14.S1+S2=S3 15.合格 16.4或5
17.48 18.126
cm2或66
cm2 19.是
20. 点拨:由勾股定理得:OP4==,∵OP1=,OP2=,OP3=,OP4=,以此类推可得OPn=,∴OP2
015=.本题考查了勾股定理的运用,解题的关键是由已知数据找到规律.
三、21.证明:假设三角形ABC的三个内角∠A、∠B、∠C中有两个直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,所以∠A=∠B=90°不成立,所以一个三角形中不能有两个角是直角.
22.解:连接AC.
在Rt△ABC中,由勾股定理得AC2=AB2+BC2,
所以AC2=42+32=25,即AC=5米.
在△ACD中,因为AC2+CD2=52+122=169=AD2.
所以△ACD是直角三角形,且∠ACD=90°.
所以S草坪=S△ABC+S△ACD=×3×4+×5×12=36(平方米).
答:这块草坪的面积是36平方米.
23.解:设AB=x米,则AC=AD+CD=AB+CD=(x+2)米.在Rt△ABC中,AC2=AB2+BC2,即(x+2)2=x2+62,解得x=8.即电线杆AB的高为8米.
24.解:设AB=3x
cm,则BC=4x
cm,AC=5x
cm,
因为△ABC的周长为36
cm,所以AB+BC+AC=36
cm,
即3x+4x+5x=36,解得x=3,
所以AB=9
cm,BC=12
cm,AC=15
cm.
因为AB2+BC2=AC2,所以△ABC是直角三角形,且∠B=90°.
过3
s时,BP=9-3×1=6(cm),BQ=2×3=6(cm),
所以S△BPQ=BP·BQ=×6×6=18(cm2).
故过3
s时,△BPQ的面积为18
cm2.
(第25题)
25.解:如图,设拖拉机行驶到C处刚好开始受到噪音的影响,行驶到D处时,结束了噪音的影响,连接AC,AD,则有CA=DA=100
m.
在Rt△ABC中,CB2=1002-802=602.
∴CB=60
m.同理BD=60
m,∴CD=120
m.
∵18
km/h=5
m/s,
∴该校受影响的时间为120÷5=24(s).
26.解:(1)a;b;c;c (2)a2;b2;c2 (3)a2+b2
(4)相等.理由:由图乙和图丙可知大正方形的边长为a+b,则面积为(a+b)2,图乙中把大正方形的面积分为了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为a,宽为b的长方形,根据面积相等得(a+b)2=a2+b2+2ab,由图丙可得(a+b)2=c2+4×ab.所以a2+b2=c2.所以图乙中①②的面积之和与图丙中③的面积相等.于是得到直角三角形三边长的关系为a2+b2=c2.
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.下列各组线段能构成直角三角形的一组是( )
A.30,40,50
B.7,12,13
C.5,9,12
D.3,4,6
2.用反证法证明“如果在△ABC中,∠C=90°,那么∠A,∠B中至少有一个角不大于45°”时,应先假设( )
A.∠A>45°,∠B>45°
B.∠A≥45°,∠B≥45°
C.∠A<45°,∠B<45°
D.∠A≤45°,∠B≤45°
(第3题)
3.如图,图中有一个正方形,此正方形的面积是( )
A.16
B.8
C.4
D.2
4.满足下列条件的△ABC不是直角三角形的是( )
A.∠A=∠B-∠C
B.∠A∶∠B∶∠C=1∶1∶2
C.b2=a2-c2
D.a∶b∶c=1∶1∶2
5.若△ABC的三边长分别为a,b,c,且满足(a-b)(a2+b2-c2)=0,则△ABC是( )
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
(第6题)
6.如图,在一块平地上,张大爷家屋前9米远处有一棵大树,在一次强风中,这棵大树从离地面6米处朝张大爷的房子方向折断倒下,量得倒下部分的长是10米,大树倒下时会砸到张大爷的房子吗( )
A.一定不会
B.可能会
C.一定会
D.以上答案都不对
7.如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线AC上的D′点处.若AB=3,AD=4,则ED的长为( )
A.
B.3
C.1
D.
(第7题)
(第8题)
(第9题)
(第10题)
8.如图,在△ABC中,AD是BC边的中线,AC=17,BC=16,AD=15,则△ABC的面积为( )
A.128
B.136
C.120
D.240
9.如图,长方体的高为9
m,底面是边长为6
m的正方形,一只蚂蚁从顶点A开始,爬向顶点B.那么它爬行的最短路程为( )
A.10
m
B.12
m
C.15
m
D.20
m
10.如图,是一种饮料的包装盒,长、宽、高分别为4
cm、3
cm、12
cm,现有一长为16
cm的吸管插入到盒的底部,则吸管露在盒外的部分h(cm)的取值范围为( )
A.3
C.2≤h≤4
D.h=4
二、填空题(每题3分,共30分)
11.若用反证法证明“有两个内角不相等的三角形不是等边三角形”,可先假设这个三角形是________.
12.在△ABC中,AC2-AB2=BC2,则∠B的度数为________.
13.如图,∠OAB=∠OBC=90°,OA=2,AB=BC=1,则OC2=________.
(第13题)
(第14题)
(第19题)
(第20题)
14.如图,直角三角形三边上的半圆形面积从小到大依次记为S1、S2、S3,则S1、S2、S3之间的关系是________.
15.木工师傅要做一个长方形桌面,做好后量得长为80
cm,宽为60
cm,对角线长为100
cm,则这个桌面________(填“合格”或“不合格”).
16.若直角三角形的两边长分别为a、b,且满足(a-3)2+|b-4|=0,则该直角三角形的斜边长为________.
17.等腰三角形ABC的腰AB为10
cm,底边BC为16
cm,则面积为________cm2.
18.在△ABC中,AB=13
cm,AC=20
cm,BC边上的高为12
cm,则△ABC的面积为________.
19.《中华人民共和国道路管理条例》规定:小汽车在城市街道上的行驶速度不得超过70
km/h.如图,一辆小汽车在一条城市街道上直道行驶时,某一时刻刚好行驶到路对面车速检测仪观测点A正前方50
m的C处,过了6
s后,行驶到B处的小汽车与车速检测仪间的距离变为130
m,请你判断:这辆小汽车________(填“是”或“否”)超速了.
20.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2;…,依照此方法继续作下去,得OP2
015=________.
三、解答题(21,22题每题8分,23,24题每题10分,25,26题每题12分,共60分)
21.用反证法证明一个三角形中不能有两个角是直角.
22.园丁住宅小区有一块草坪如图,已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,求这块草坪的面积.
(第22题)
23.如图,将断落的电话线拉直,使其一端在电线杆顶端A处,另一端落在地面C处,这时测得BC=6米,再把电话线沿电线杆拉扯,使AD=AB,并量出电话线剩余部分(即CD)的长为2米,你能由此算出电线杆AB的高吗?
(第23题)
24.如图,在△ABC中,AB∶BC∶CA=3∶4∶5,且周长为36
cm,点P从点A开始沿AB边向B点以每秒1
cm的速度移动;点Q从点B开始沿BC边向点C以每秒2
cm的速度移动,如果P,Q同时出发,问过3
s时,△BPQ的面积为多少?
(第24题)
25.如图,公路MN和公路PQ在点P处交汇,公路PQ上点A处有一学校,点A到公路MN的距离为80
m,现有一拖拉机在公路MN上以18
km/h的速度沿PN方向行驶,拖拉机行驶时周围100
m以内都会受到噪音的影响,试问该校受影响的时间为多长?
(第25题)
26.图甲是任意一个直角三角形ABC,它的两条直角边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为(a+b)的正方形内.
(1)图乙、图丙中①②③都是正方形.由图可知:①是以________为边长的正方形,②是以________为边长的正方形,③的四条边长都是________,且每个角都是直角,所以③是以________为边长的正方形;
(2)图乙中①的面积为________,②的面积为________,图丙中③的面积为________;
(3)图乙中①②的面积之和为________;
(4)图乙中①②的面积之和与图丙中③的面积有什么关系?为什么?由此你能得到关于直角三角形三边长的关系吗?
(第26题)
答案
一、1.A 2.A 3.B 4.D 5.D 6.A 7.A 8.C 9.C 10.B
二、11.等边三角形 12.90° 13.6
14.S1+S2=S3 15.合格 16.4或5
17.48 18.126
cm2或66
cm2 19.是
20. 点拨:由勾股定理得:OP4==,∵OP1=,OP2=,OP3=,OP4=,以此类推可得OPn=,∴OP2
015=.本题考查了勾股定理的运用,解题的关键是由已知数据找到规律.
三、21.证明:假设三角形ABC的三个内角∠A、∠B、∠C中有两个直角,不妨设∠A=∠B=90°,则∠A+∠B+∠C=90°+90°+∠C>180°,这与三角形内角和为180°相矛盾,所以∠A=∠B=90°不成立,所以一个三角形中不能有两个角是直角.
22.解:连接AC.
在Rt△ABC中,由勾股定理得AC2=AB2+BC2,
所以AC2=42+32=25,即AC=5米.
在△ACD中,因为AC2+CD2=52+122=169=AD2.
所以△ACD是直角三角形,且∠ACD=90°.
所以S草坪=S△ABC+S△ACD=×3×4+×5×12=36(平方米).
答:这块草坪的面积是36平方米.
23.解:设AB=x米,则AC=AD+CD=AB+CD=(x+2)米.在Rt△ABC中,AC2=AB2+BC2,即(x+2)2=x2+62,解得x=8.即电线杆AB的高为8米.
24.解:设AB=3x
cm,则BC=4x
cm,AC=5x
cm,
因为△ABC的周长为36
cm,所以AB+BC+AC=36
cm,
即3x+4x+5x=36,解得x=3,
所以AB=9
cm,BC=12
cm,AC=15
cm.
因为AB2+BC2=AC2,所以△ABC是直角三角形,且∠B=90°.
过3
s时,BP=9-3×1=6(cm),BQ=2×3=6(cm),
所以S△BPQ=BP·BQ=×6×6=18(cm2).
故过3
s时,△BPQ的面积为18
cm2.
(第25题)
25.解:如图,设拖拉机行驶到C处刚好开始受到噪音的影响,行驶到D处时,结束了噪音的影响,连接AC,AD,则有CA=DA=100
m.
在Rt△ABC中,CB2=1002-802=602.
∴CB=60
m.同理BD=60
m,∴CD=120
m.
∵18
km/h=5
m/s,
∴该校受影响的时间为120÷5=24(s).
26.解:(1)a;b;c;c (2)a2;b2;c2 (3)a2+b2
(4)相等.理由:由图乙和图丙可知大正方形的边长为a+b,则面积为(a+b)2,图乙中把大正方形的面积分为了四部分,分别是:边长为a的正方形,边长为b的正方形,还有两个长为a,宽为b的长方形,根据面积相等得(a+b)2=a2+b2+2ab,由图丙可得(a+b)2=c2+4×ab.所以a2+b2=c2.所以图乙中①②的面积之和与图丙中③的面积相等.于是得到直角三角形三边长的关系为a2+b2=c2.
