2.4线段、角的轴对称 复习课件

(共20张PPT)
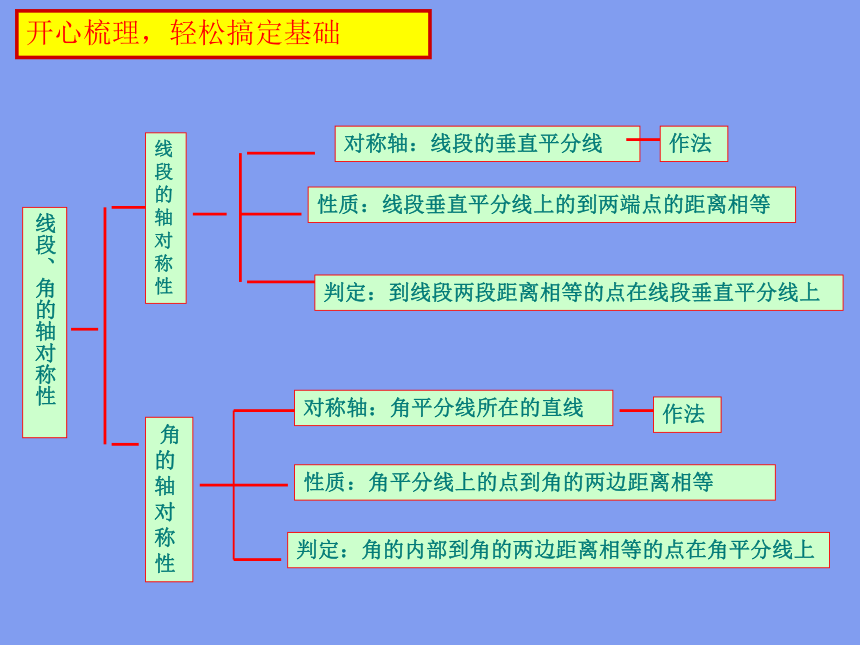
开心梳理，轻松搞定基础
性质：线段垂直平分线上的到两端点的距离相等
线段的轴对称性
判定：角的内部到角的两边距离相等的点在角平分线上
角的轴对称性
对称轴：线段的垂直平分线
判定：到线段两段距离相等的点在线段垂直平分线上
性质：角平分线上的点到角的两边距离相等
对称轴：角平分线所在的直线
线段、角的轴对称性
作法
作法
1.角是____________ 图形，角的对称轴是 _____________所在的直线
3.如图，点P在∠AOB内部， PE⊥OB于点E，PD⊥OA于点D,且PD=PE.
若∠DOP=20°，则∠COB=＿＿ ,∠OPE=＿＿；
B
E
P
O
D
A
C
2.如图，OC是∠AOB的平分线，P是OC上一点， PE⊥OB于点E,PD⊥OA于点D，PE=6㎝，
PD= ㎝
角平分线上的点到角两边的距离相等
20°
70°
角的内部到角两边的距离相等的点在角的平分线上的点
角平分线
轴对称
6
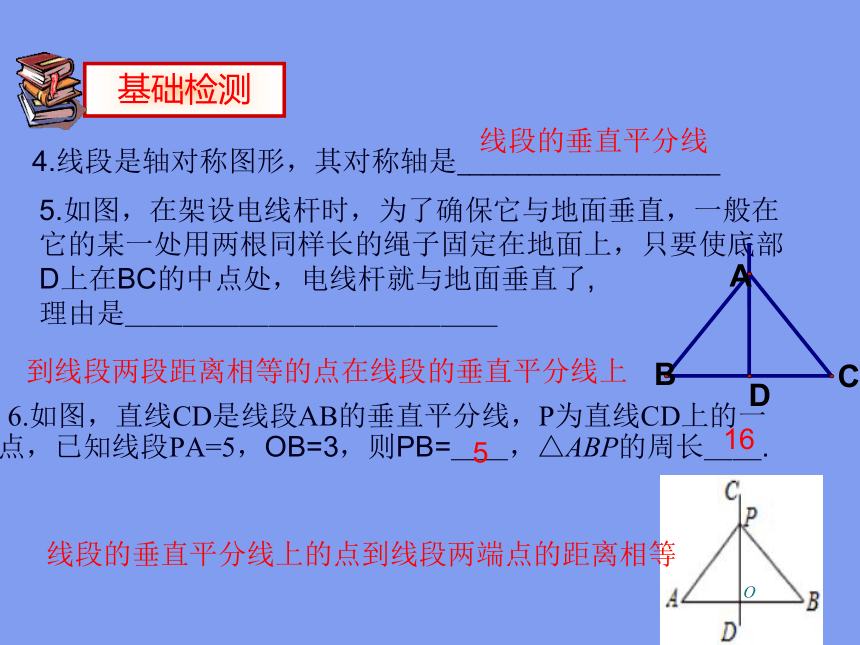
基础检测
6.如图，直线CD是线段AB的垂直平分线，P为直线CD上的一点，已知线段PA=5，OB=3，则PB=＿＿，△ABP的周长＿＿.
5.如图，在架设电线杆时，为了确保它与地面垂直，一般在它的某一处用两根同样长的绳子固定在地面上，只要使底部D上在BC的中点处，电线杆就与地面垂直了,
理由是＿＿＿＿＿＿＿＿＿＿＿＿＿
到线段两段距离相等的点在线段的垂直平分线上
D
B
C
A
O
线段的垂直平分线上的点到线段两端点的距离相等
4.线段是轴对称图形，其对称轴是______________________
5
16
线段的垂直平分线
基础检测
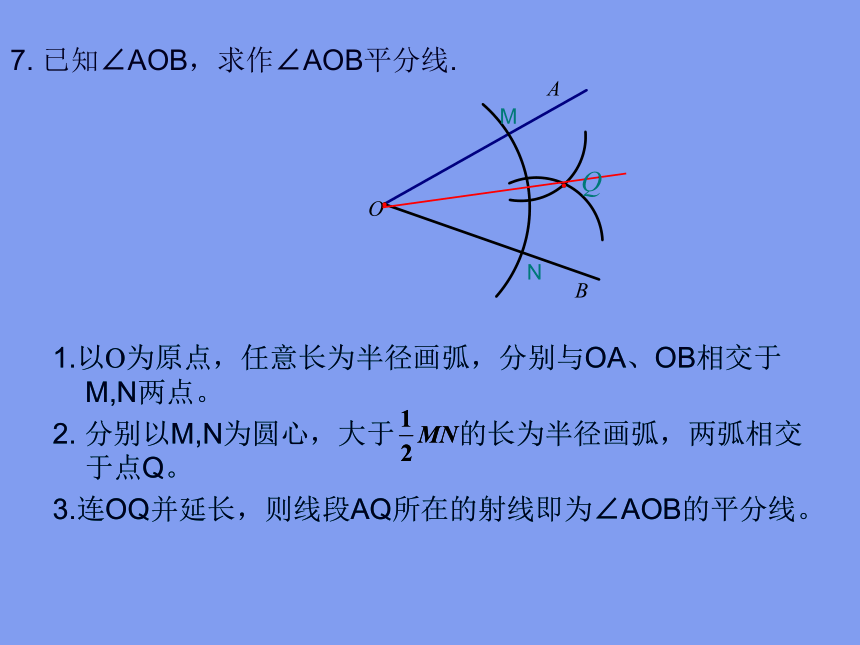
1.以O为原点，任意长为半径画弧，分别与OA、OB相交于M,N两点。
2. 分别以M,N为圆心，大于 的长为半径画弧，两弧相交于点Q。
3.连OQ并延长，则线段AQ所在的射线即为∠AOB的平分线。
7. 已知∠AOB，求作∠AOB平分线.
M
N
Q
1.以O为原点，任意长为半径画弧，分别与OA、OB相交于M,N两点。
2. 分别以M,N为圆心，大于 的长为半径画弧，两弧相交于点Q。
3.连OQ并延长，则线段AQ所在的射线即为∠AOB的平分线。
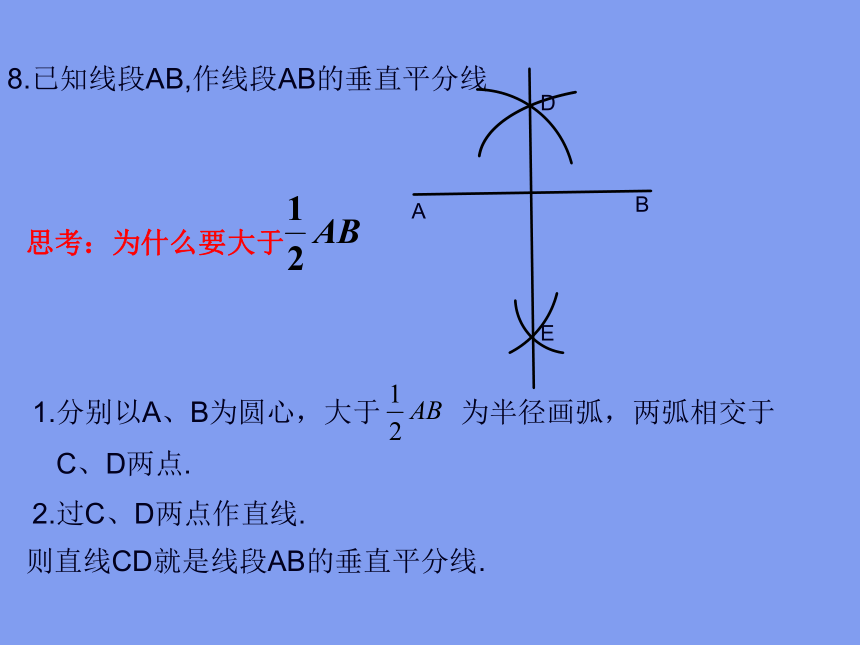
8.已知线段AB,作线段AB的垂直平分线
A
B
E
D
1.分别以A、B为圆心，大于 为半径画弧，两弧相交于
C、D两点.
2.过C、D两点作直线.
则直线CD就是线段AB的垂直平分线.
思考：为什么要大于
如图，在△ABC中，AB=AC， D为BC的中点，DE⊥AB于
(2)求证：DE=DF
典例分析1
证明：∵ D为BC的中点 ∴BD=CD
在△ABD与△ACD中
∴∠1=∠2
∴D在∠BAC平分线上
又∵ DE⊥AB，DF⊥AC
∴DE=DF
转化思想：
证边等转化成证明角等
1
2
∴△ABD≌△ACD
角的平分线上的点到角的两边距离相等
(1)根据条件你能得到哪些正确结论？
E，DF⊥AC于F.
如图，在△ABC中，AB=AC， D为BC上一点，DE⊥AB于E，DF⊥AC于F， 且DE=DF.求证： D为BC中点.
转化思想：
证边等转化成证明三角形全等
变 式 训 练
角的内部到角的两边距离相等的点在角的平分线上
1
2
如图，△ABC中，DE、FG分别是边AB 、 AC的垂直平分线，
典例分析2
（1）根据条件，你能得到哪些正确结论？
（2）你能通过添加哪一条线段的长，求出△AEG的周长？
（3） 若∠BAC=110° ，则∠EAG=__________
(2) 添加BC长度可 以求出△AEG的周长.
∵DE、FG分别是边AB 、 AC的垂直平分线
∴AE+EG+AG=BE+EG+CG
=BC
∴BE=AE,AG=CG
∴BE=AE,AG=CG
解（1）略
数学思想：转化思想
数形结合思想
(3)若∠BAC=110° ，则∠EAG=_______
40°
解 题 过 程
1. 到三角形的三个顶点距离相等的点是（ ）
A、三角形的三条高线的交点
B、三角形的三条中线的交点
C、三角形的三条内角平分线的交点
D、三角形三边垂直平分线的交点
2.到三角形的三边距离相等的点是（ ）
A、三角形的三条高线的交点 B、三角形的三条中线的交点 C、三角形的三条内角平分线的交点 D、三角形三边垂直平分线的交点
巩 固 练 习
如图，己知
，
AC
、
AB
于
、
，
BC=10cm,
∠
A=49
，求△
3.如图，已知AB=AC，DE垂直平分AB交AC、AB于E、D两点，若AB=12cm，BC=10cm，∠A=50 °.
（1）求△BCE的周长
（2）∠ABE=_______
(3) 求∠EBC的度数
巩 固 练 习
A
B
C
4.尺规作图：
（1）在BC上找一点P，使点P到AB和AC的距离相等；
（2）在射线AP上找一点Q，使QB=QC.
巩 固 练 习
已知：如图ΔABC （1）找一点P,使点P到AB、AC的两边距离相等且到B、C两点距离相等 （2）过P作PD⊥AB,PE⊥AC，若PD=2 cm，则PE=__________ （3）在（2）的条件下，若Q为射线AC上任一点，则PQ的值是（ ） A.PQ>2 B. PQ<2 C. PQ≥2 D. PQ不确定
2
C
Q
典例分析3
(4) 作P关于射线AB的对称点G，关于射线的对称点H，若∠BAC=30，则∠GAH=————
拓展提高
已知∠AOB=90°，在∠AOB的平分线OM上有一点C，将一个三角板的直角顶点与C重合，它的两条直角边分别与OA、OB（或它们的反向延长线）相交于点D、E．
（1）当三角板绕点C旋转到CD与OA垂直时（如图1），易证：CD=CE，请说明理由．
（2）当三角板绕点C旋转到CD与OA不垂直时，在图2这种情况下，上述结论是否还成立？若成立，请给予证明．
（3）当三角板绕点C旋转到CD与OA不垂直时，在图3这种情况下，上述结论是否还成立？请写出你的猜想，不需证明．
拓展提高
数学思想：
课堂小结
转化思想
数形结合思想
类比思想
基本技能
发散思维能力
逻辑推理能力
基本作图能力