2.2有理数与无理数 课件

课件20张PPT。2.2有理数与无理数初中数学 七上知识回顾我们已经学过了哪些数？有理数出现的几种形式：
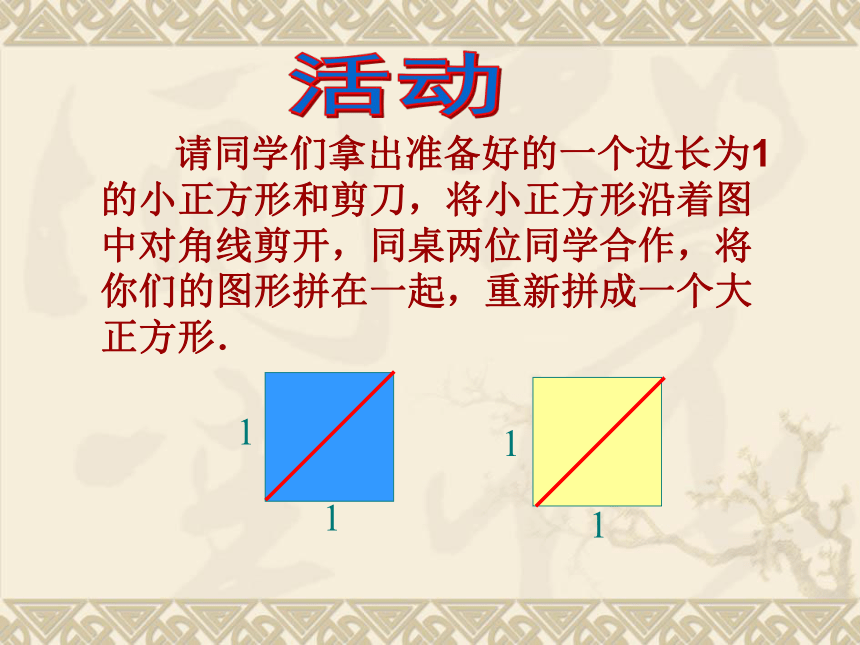
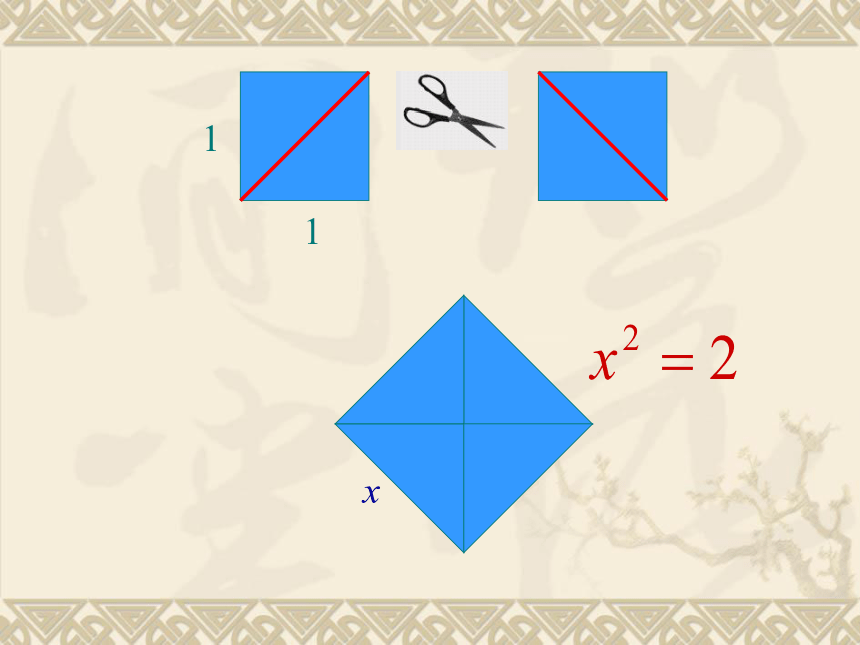
整数、分数、有限小数、无限循环小数可以化为分数形式“ （m、n是整数，n≠0）”的数叫做有理数3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 ···＝ 请同学们拿出准备好的一个边长为1的小正方形和剪刀，将小正方形沿着图中对角线剪开，同桌两位同学合作，将你们的图形拼在一起，重新拼成一个大正方形．1111活动11x能否是整数 ？
所以x是1-2之间的一个数， 不是整数
x会不会是分数？

…
x也不可能是分数. 1.4＜x＜1.5
1.41＜ x ＜1.42
1.414＜ x ＜1.415
… …无限不循环小数叫做无理数 … =3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 ···
x=1.4142135623730950488016887242096980785696718753769480731766797379907324784621 ··· 1.4＜x＜1.5
1.41＜ x ＜1.42
1.414＜ x ＜1.415
无理数的发现 早在公元前，古希腊数学家毕达哥拉斯认为万物皆“数”，即“宇宙间的一切现象都能归结为整数或整数之比”，也就是一切现象都可用有理数去描述.后来，这个学派中的一个叫希伯索斯的成员发现边长为1的正方形的对角线的长不能用整数或整数之比来表示，这个发现动摇了毕达哥拉斯学派的信条，据说为此希伯索斯被投进了大海，他为真理而献出了宝贵的生命，但真理是不可战胜的，后来古希腊人终于正视了希伯索斯的发现.也就是我们前面谈过
的 = 2 中的 不是有理数.2小故事0.585885888588885888885 (相邻两个5之间8的个数逐次加1)…有理数与无理数的概念： 可以化为分数形式“（m、n是整数，n≠0）” 的数叫做有理数 无限不循环小数叫做无理数 无理数是无限不循环小数，抓住无限不循环
有理数是可以化为分数形式的数，
包括有限小数、无限循环小数、分数、 整 数.有理数与无理数的区别：将下列各数填入相应的括号内：正数集合：｛ …｝ 负数集合：｛ …｝
有理数集合：｛ …｝
无理数集合：｛ …｝例题-2.5, 0, 8，- 2， ????，0.7， ， -0.
-1.121121112 ， ?? ???? ???80.7，，，-2.5, - 2， ????， -0.

-1.121121112，…-2.5, 0, 8，- 2，0.7， ， -0. ?， ， -1.121121112……试一试
1 .判断对错
（1） 有限小数都是有理数； （ ）?????
?（2） 无限小数都是无理数； （ ）
（3） 正数包括正有理数与正无理数 （ ）
（4） 是无理数. （ ）√√×√
2 .把下列各数分别填入相应的大括号内：
－ 6，0，＋3， －0.333 ， π
－1.41421356···，3.141．有理数集合：｛ ··· ｝
无理数集合：{ ··· }π ，－1.41421356···
－ 6，0，＋3，
-0.333 ，3.141，3 .以下各正方形的边长是无理数的是（ ） A 面积为 1 的正方形；?????
B 面积为 4 的正方形；
C 面积为 3 的正方形；???????
D 面积为 16 的正方形.C
对 于“分数都是有理数”，有同学提出了如下的疑问，请判断他的说法是否正确．
甲同学认为不一定，如 计算器计算显示的满屏结果是3.142857143，后边的数还没显示完，好像是无限不循环小数，是无理数．
4.讨论 =3.142857142857··· 乙同学也认为不一定，如 就是无理数． 这节课，我的收获是---小结与回顾2 .感受数学思想方法：
数形结合、分类思想、夹逼思想1 .数的辨别方法：
无理数是无限不循环小数，抓住“无限不循环”
有理数抓住可化为“分数形式”，或者从数的表现形式：有限小数或无限循环小数、整数、分数.
作业：
必做 书本17页 练一练；习题1
选做 阅读17页 读一读将两个边长为2的小正方形，沿图中红线剪一剪，重新拼成如图所示的大正方形，大正方形边长x是一个无理数，你能估计x的保留两位小数的近似值吗？保留3位小数的近似值呢？
拓展延伸