河南省周口项城市八年级数学下册17.2勾股定理的逆定理(第2课时)教学课件(新版)新人教版
文档属性
| 名称 | 河南省周口项城市八年级数学下册17.2勾股定理的逆定理(第2课时)教学课件(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-25 19:52:43 | ||
图片预览





文档简介
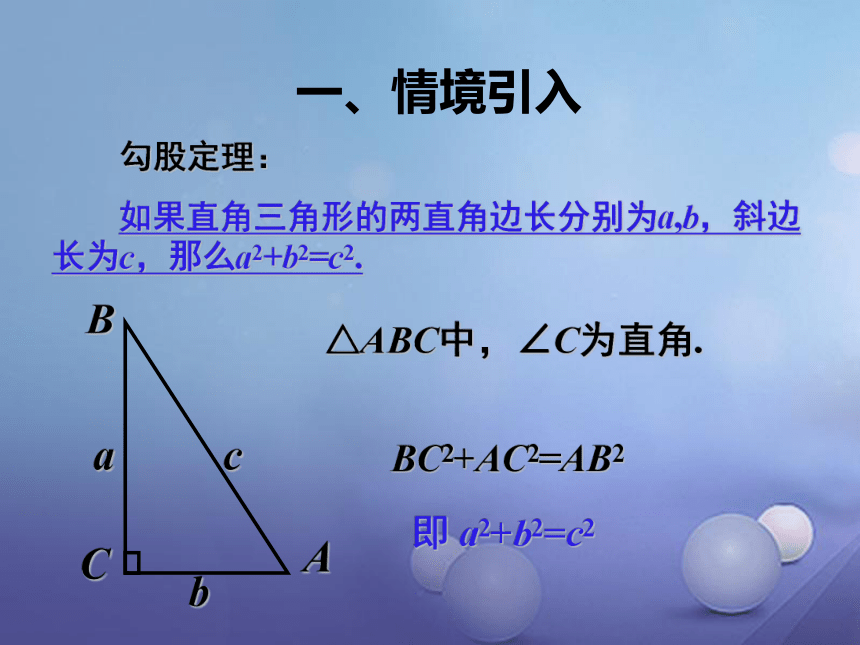
课件14张PPT。 17.2 勾股定理的逆定理第十七章 勾股定理 第2课时一、情境引入 勾股定理:
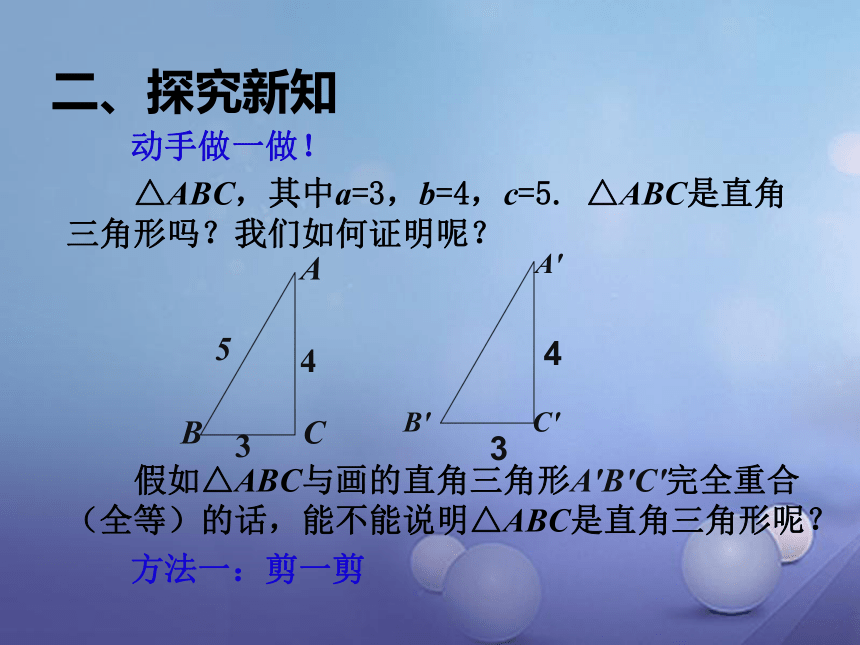
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.abc△ABC中,∠C为直角.BC2+AC2=AB2即 a2+b2=c2一、情境引入 猜想:命题2 如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.命题2 正确吗? 二、探究新知动手做一做! △ABC,其中a=3,b=4,c=5. △ABC是直角三角形吗?我们如何证明呢?方法一:剪一剪 假如△ABC与画的直角三角形A′B′C′完全重合(全等)的话,能不能说明△ABC是直角三角形呢?证明:画△ A′B′C′,使A′C′=4,B′C′=3, ∠C′=90°,∴A′B′=5, △ABC,其中a=3,b=4,c=5. △ABC是直角三角形吗?我们如何证明呢?∴在△ABC和△A′B′C′中,AB=A′B′, AC=A′C′,
BC=B′C′,∴ △ABC≌ △A′B′C′.∴∠C=∠C′=90°.即△ABC是直角三角形.方法二:用推理证明的方法来论证两三角形是全等的.二、探索一般性的结论 勾股定理的逆定理
如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.古埃及人得到直角的方法通过证明,得到定理 得到猜想画图(操作)验证 问题:
原命题成立,逆命题一定成立吗?你能举出一些相关的例子吗? 一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理“互为逆定理”. 原命题成立的,它的逆命题也可能不成立,如命题“对顶角相等”成立,它的逆命题“如果两个角相等,那么这两个是对顶角”不成立.解:∵82 +152 =289, 例 判断由线段a,b,c组成的三角形是不是直角三角形. ∴由线段a,b,c组成的三角形是直角三角形.应用新知a=15,b=8,c=17;a=13,b=14,c=15.172 =289,∴a2+b2=c2,两条较短直角边的平方和较长直角边的平方 能过成为直角三角形三条边长的三个正整数,称为勾股数.
请举出两对互为逆定理的命题.三、巩固练习 通过这节课的学习,你有什么收获?你还有什么困惑? 四、小结1.必做题:教材习题17.2第3题.五、作业设计2.选做题:教材习题17.2第7题. (1)下列各组数中,不能组成直角三角形的是( )3.备选题:A.4,40,41 B.7,24,25
C.13,84,85 D.9,27,31 (2)已知在△ABC中,AB=7,BC=24,AC=25,则 =90°. (3)如右图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,求证∠AEF=90°(提示:连接AF). 谢谢大家
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.abc△ABC中,∠C为直角.BC2+AC2=AB2即 a2+b2=c2一、情境引入 猜想:命题2 如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.命题2 正确吗? 二、探究新知动手做一做! △ABC,其中a=3,b=4,c=5. △ABC是直角三角形吗?我们如何证明呢?方法一:剪一剪 假如△ABC与画的直角三角形A′B′C′完全重合(全等)的话,能不能说明△ABC是直角三角形呢?证明:画△ A′B′C′,使A′C′=4,B′C′=3, ∠C′=90°,∴A′B′=5, △ABC,其中a=3,b=4,c=5. △ABC是直角三角形吗?我们如何证明呢?∴在△ABC和△A′B′C′中,AB=A′B′, AC=A′C′,
BC=B′C′,∴ △ABC≌ △A′B′C′.∴∠C=∠C′=90°.即△ABC是直角三角形.方法二:用推理证明的方法来论证两三角形是全等的.二、探索一般性的结论 勾股定理的逆定理
如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.古埃及人得到直角的方法通过证明,得到定理 得到猜想画图(操作)验证 问题:
原命题成立,逆命题一定成立吗?你能举出一些相关的例子吗? 一般地,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理“互为逆定理”. 原命题成立的,它的逆命题也可能不成立,如命题“对顶角相等”成立,它的逆命题“如果两个角相等,那么这两个是对顶角”不成立.解:∵82 +152 =289, 例 判断由线段a,b,c组成的三角形是不是直角三角形. ∴由线段a,b,c组成的三角形是直角三角形.应用新知a=15,b=8,c=17;a=13,b=14,c=15.172 =289,∴a2+b2=c2,两条较短直角边的平方和较长直角边的平方 能过成为直角三角形三条边长的三个正整数,称为勾股数.
请举出两对互为逆定理的命题.三、巩固练习 通过这节课的学习,你有什么收获?你还有什么困惑? 四、小结1.必做题:教材习题17.2第3题.五、作业设计2.选做题:教材习题17.2第7题. (1)下列各组数中,不能组成直角三角形的是( )3.备选题:A.4,40,41 B.7,24,25
C.13,84,85 D.9,27,31 (2)已知在△ABC中,AB=7,BC=24,AC=25,则 =90°. (3)如右图,在正方形ABDC中,E是CD的中点,F为BD上一点,且BF=3FD,求证∠AEF=90°(提示:连接AF). 谢谢大家
