河南省周口项城市八年级数学下册18.1.2平行四边形的判定(第1课时)教学课件(新版)新人教版
文档属性
| 名称 | 河南省周口项城市八年级数学下册18.1.2平行四边形的判定(第1课时)教学课件(新版)新人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-25 20:00:56 | ||
图片预览





文档简介
课件15张PPT。118.1.2 平行四边形的判定
第1课时
第十八章 平行四边形18.1 平行四边形1一、温故知新,引入新课
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?写出这条性质定理.
3.它的逆命题是什么?你认为它成立吗?11.两组对边分别平行的四边形是平行四边形.2.平行四边形的两组对边分别相等.逆命题:两组对边分别相等的四边形是平行四边形.这个命题是否成立?1二、猜想证明,探索新知动手操作,实验探究:
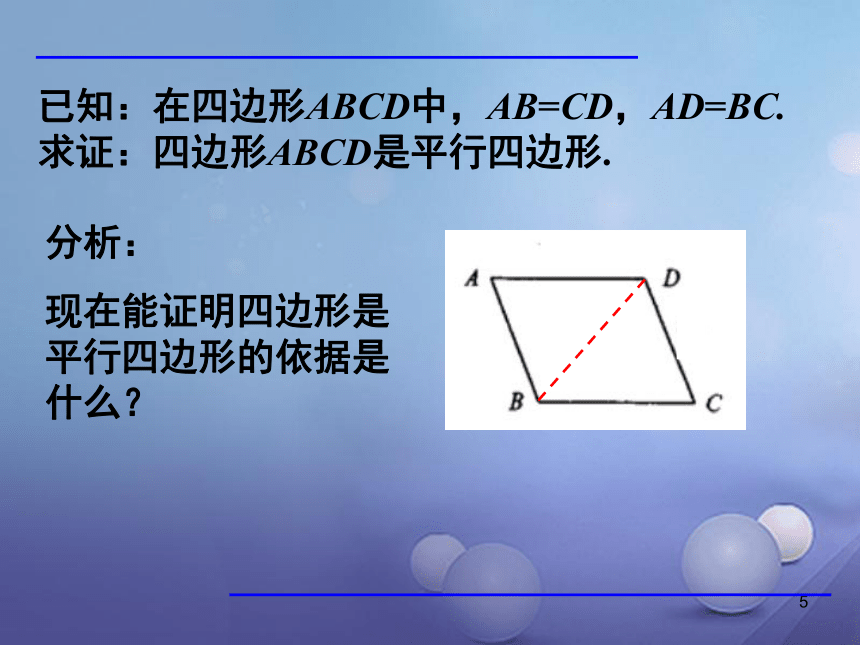
每人拿出一条长20cm的线,想一想,能否将此线分成四段,然后首尾相连,构成一个平行四边形? 1已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.分析:
现在能证明四边形是平行四边形的依据是什么? 1在四边形ABCD中,
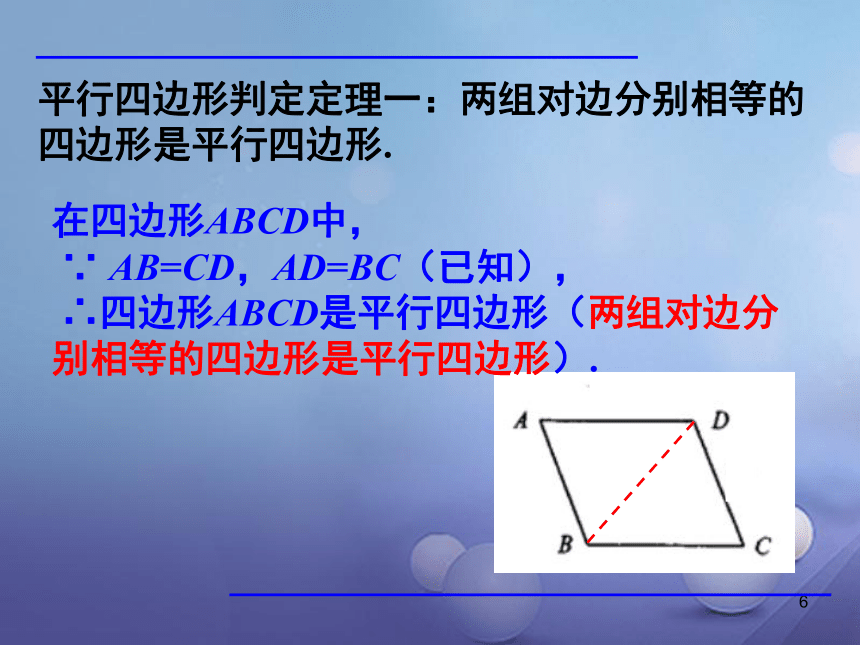
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).平行四边形判定定理一:两组对边分别相等的四边形是平行四边形. 1探索其他判定方法: 你知道平行四边形还有哪些判定方法吗?说出这些命题,并尝试证明. 命题1:两组对角分别相等的四边形是平行四边形.命题2:对角线互相平分的四边形是平行四边形.请尝试用不同方法来证明.1平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D(已知),
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).1平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.在四边形ABCD中,对角线AC、BD交于点O.
∵ OA= OC, OB=OD(已知),
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).1例3 如图, ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF. 求证:四边形BFDE是平行四边形. 三、应用新知,巩固提高□1分析:
要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便. 本题很明显是对角线条件比较突出,因此用判定定理三证明比较简便. 1提问:本题还有其他证法吗?
请从定义、几个判定定理分别考虑. 1四、本课小结 本节课你学习了哪些知识?
获得了哪些研究问题的方法?
你有什么收获 ?1知识上:
平行四边形的判定方法有定义、三个判定定理,分别从对边、对角和对角线来研究. 1方法上:
将四边形转化为三角形是一般方法,体现了转化思想;
平行四边形的性质和判定定理是互逆命题,今后研究其他图形会类比这个研究方法进行;
先从简单问题入手研究,再扩展到其他问题,由简单到复杂.
第1课时
第十八章 平行四边形18.1 平行四边形1一、温故知新,引入新课
1.平行四边形的定义是什么?
2.平行四边形的对边具有什么性质?写出这条性质定理.
3.它的逆命题是什么?你认为它成立吗?11.两组对边分别平行的四边形是平行四边形.2.平行四边形的两组对边分别相等.逆命题:两组对边分别相等的四边形是平行四边形.这个命题是否成立?1二、猜想证明,探索新知动手操作,实验探究:
每人拿出一条长20cm的线,想一想,能否将此线分成四段,然后首尾相连,构成一个平行四边形? 1已知:在四边形ABCD中,AB=CD,AD=BC.
求证:四边形ABCD是平行四边形.分析:
现在能证明四边形是平行四边形的依据是什么? 1在四边形ABCD中,
∵ AB=CD,AD=BC(已知),
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).平行四边形判定定理一:两组对边分别相等的四边形是平行四边形. 1探索其他判定方法: 你知道平行四边形还有哪些判定方法吗?说出这些命题,并尝试证明. 命题1:两组对角分别相等的四边形是平行四边形.命题2:对角线互相平分的四边形是平行四边形.请尝试用不同方法来证明.1平行四边形判定定理二:
两组对角分别相等的四边形是平行四边形.
在四边形ABCD中,
∵ ∠A= ∠C, ∠B= ∠D(已知),
∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形).1平行四边形判定定理三:
对角线互相平分的四边形是平行四边形.在四边形ABCD中,对角线AC、BD交于点O.
∵ OA= OC, OB=OD(已知),
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).1例3 如图, ABCD的对角线AC、BD相交于点O,E,F是AC上的两点,并且AE=CF. 求证:四边形BFDE是平行四边形. 三、应用新知,巩固提高□1分析:
要证四边形是平行四边形,看已知条件给的信息是对边、对角,还是对角线,然后进一步分析利用哪个途径证明更方便. 本题很明显是对角线条件比较突出,因此用判定定理三证明比较简便. 1提问:本题还有其他证法吗?
请从定义、几个判定定理分别考虑. 1四、本课小结 本节课你学习了哪些知识?
获得了哪些研究问题的方法?
你有什么收获 ?1知识上:
平行四边形的判定方法有定义、三个判定定理,分别从对边、对角和对角线来研究. 1方法上:
将四边形转化为三角形是一般方法,体现了转化思想;
平行四边形的性质和判定定理是互逆命题,今后研究其他图形会类比这个研究方法进行;
先从简单问题入手研究,再扩展到其他问题,由简单到复杂.
