单元测试 高一数学人教版必修2(第01章 空间几何体) Word版含解析
文档属性
| 名称 | 单元测试 高一数学人教版必修2(第01章 空间几何体) Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-06-29 21:55:52 | ||
图片预览


文档简介
绝密★启用前
人教版必修2
第01章
空间几何体
单元测试卷
(时间:120分钟 满分:150分)
第Ⅰ卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【题文】截一个几何体,各个截面都是圆面,则这个几何体一定是()
A.圆柱B.圆锥C.球D.圆台
2.【题文】一个直角三角形绕斜边所在直线旋转360°形成的空间几何体为()
A.一个圆锥
B.一个圆锥和一个圆柱
C.两个圆锥
D.一个圆锥和一个圆台
3.【题文】用一个平行于棱锥底面的平面截这个棱锥,截得的棱台上、下底面面积比为,截去的棱锥的高是,则棱台的高是()
A.
B.
C.
D.
4.【题文】中央电视台有一个非常受欢迎的
( http: / / www.21cnjy.com )娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为()
( http: / / www.21cnjy.com )
A.
B.
C.
D.
5.【题文】利用斜二测画法得到的:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上结论正确的是()
A.①②
B.①
C.③④
D.①②③④
6.【题文】某几何体的三视图如图所示,则该几何体的体积是()
( http: / / www.21cnjy.com )
A.B.C.D.
7.【题文】一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底均为1的等腰梯形,则这个平面图形的面积为()
A.
B.
C.
D.
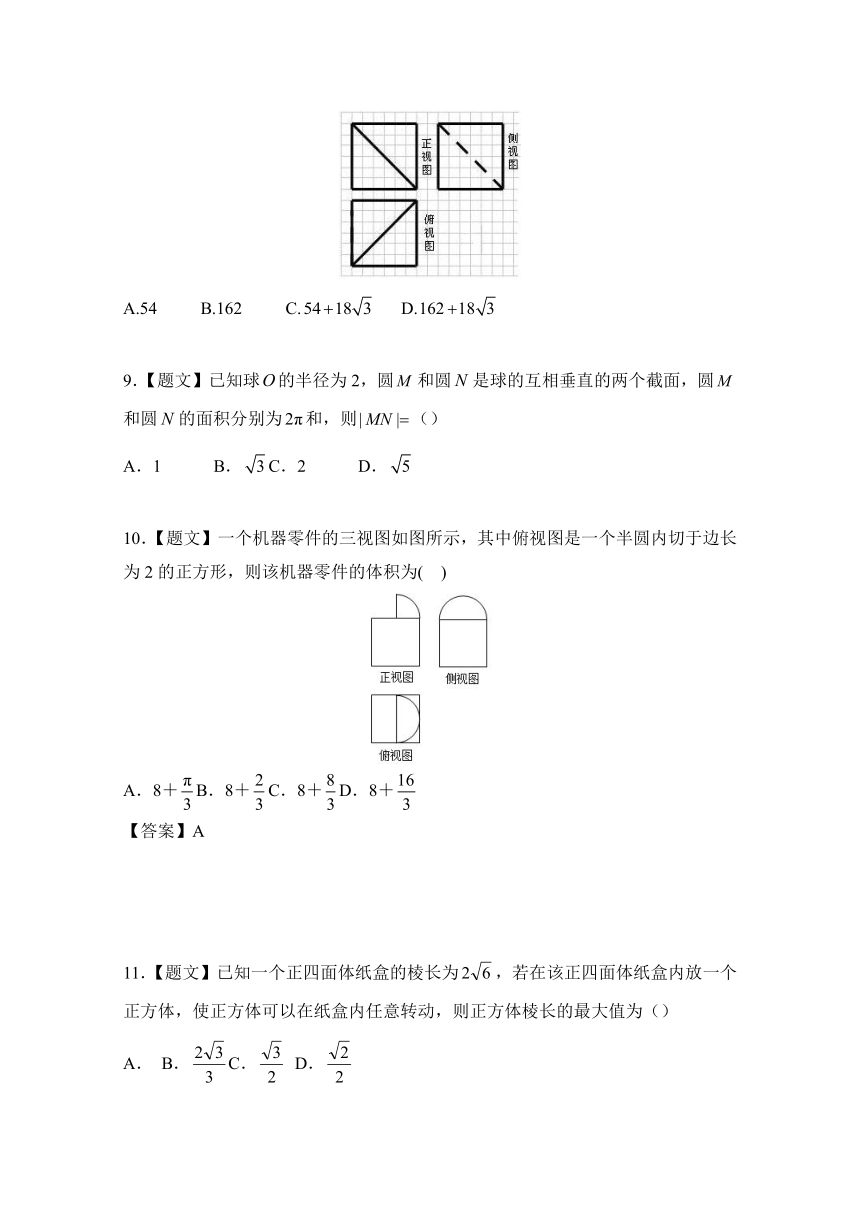
8.【题文】如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为()
( http: / / www.21cnjy.com )
A.54
B.162
C.
D.
9.【题文】已知球的半径为2,圆和圆是球的互相垂直的两个截面,圆和圆的面积分别为和,则()
A.1
B.C.2
D.
10.【题文】一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为(
)
( http: / / www.21cnjy.com )
A.8+B.8+C.8+D.8+
【答案】A
11.【题文】已知一个正四面体纸盒的棱长为,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为()
A.
B.C.
D.
12.【题文】将一张边长为6
cm的纸片按
( http: / / www.21cnjy.com )如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是()
( http: / / www.21cnjy.com )
A.
B.
C.
D.
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)
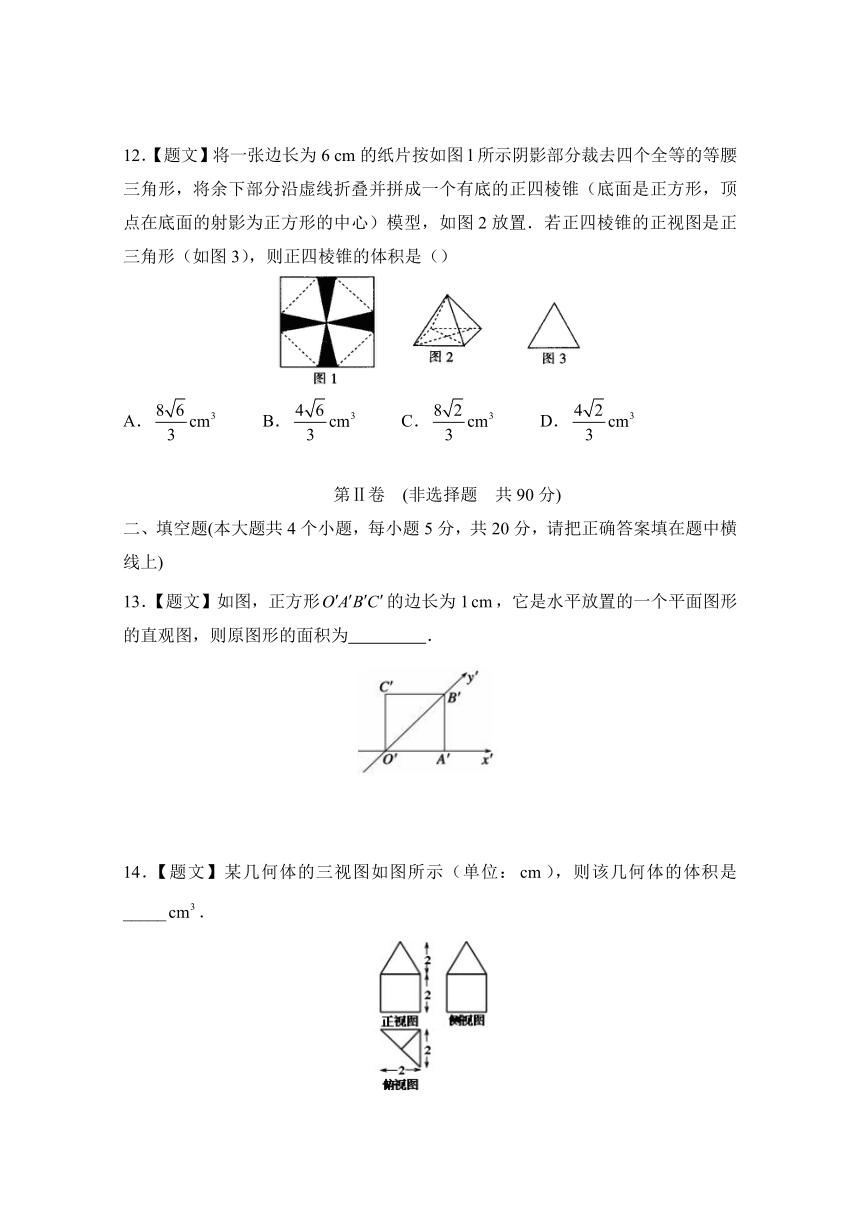
13.【题文】如图,正方形的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积为
.
( http: / / www.21cnjy.com )
14.【题文】某几何体的三视图如图所示(单位:),则该几何体的体积是_____.
( http: / / www.21cnjy.com )
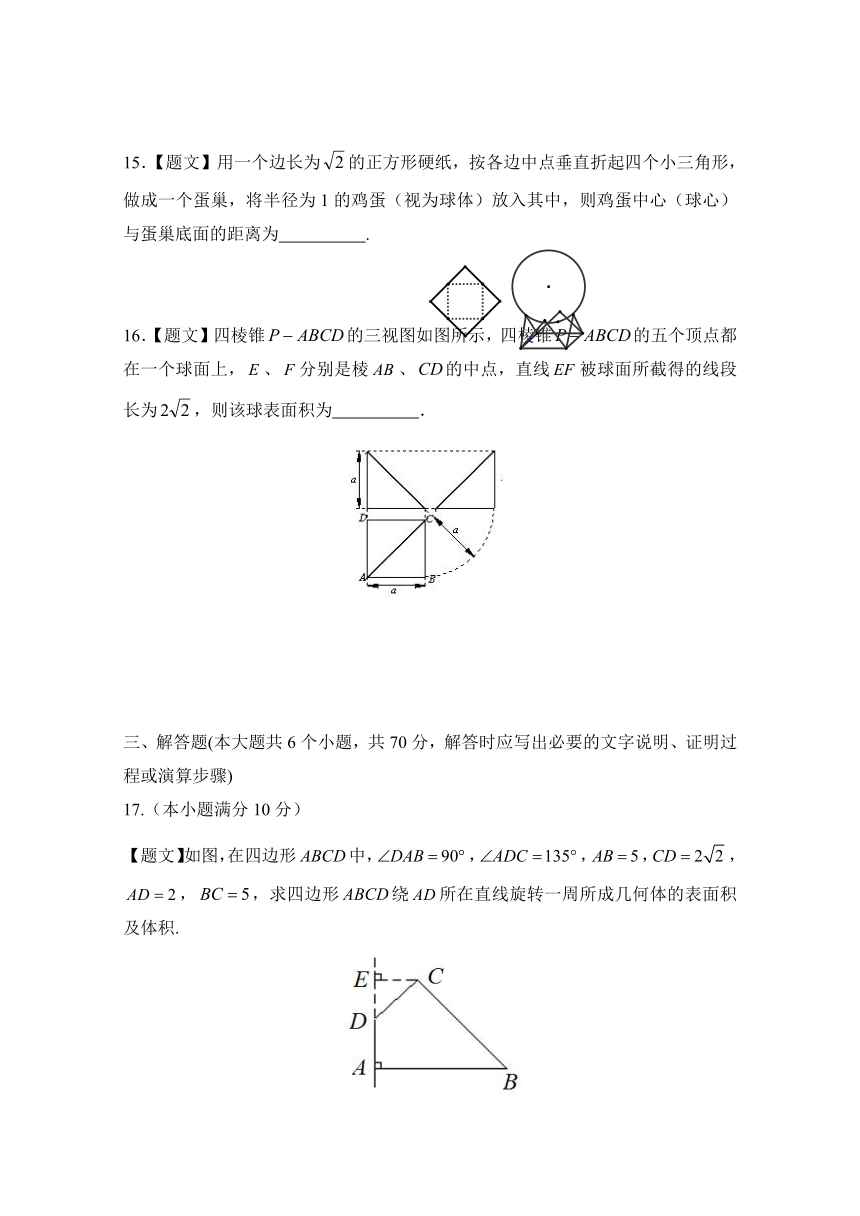
15.【题文】用一个边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为
.
16.【题文】四棱锥的三视图如图所示,四棱锥的五个顶点都在一个球面上,、分别是棱、的中点,直线被球面所截得的线段长为,则该球表面积为
.
( http: / / www.21cnjy.com )
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)
【题文】如图,在四边形中,,,,,,,求四边形绕所在直线旋转一周所成几何体的表面积及体积.
( http: / / www.21cnjy.com )
18.(本小题满分12分)
【题文】设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
19.(本小题满分12分)
【题文】用斜二测画法画出图中水平放置的图形的直观图.
( http: / / www.21cnjy.com )
20.(本小题满分12分)
【题文】已知一个几何体的三视图如图所示.
( http: / / www.21cnjy.com )
(1)求此几何体的表面积;
(2)如果点在正视图中所示位置:为所在线段中点,为顶点,求在几何体表面上,从点到点的最短路径的长.
21.(本小题满分12分)
【题文】已知底面为正方形的四棱锥P-ABC
( http: / / www.21cnjy.com )D如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4
cm的全等的等腰直角三角形.
( http: / / www.21cnjy.com )
(1)根据图(2)所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求PA.
22.(本小题满分12分)
【题文】已知四棱锥中,底面为矩形,底面,,,为的中点.
( http: / / www.21cnjy.com )
(1)在图中作出平面与的交点,并指出点所在位置(不要求给出理由);
(2)求平面将四棱锥分成上下两部分的体积比.
人教版必修2
第01章
空间几何体
单元卷
答题卡
注意事项:
1.
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己姓名和班级填写在答题卡上。
2.
选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案信息号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.
非选择题必须用黑色字
( http: / / www.21cnjy.com )迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.
考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、选择题
1、
A
]
B
]
C
]
D
]2、
A
]
B
]
C
]
D
]3、
A
]
B
]
C
]
D
]4、
A
]
B
]
C
]
D
]5、
A
]
B
]
C
]
D
]
6、
A
]
B
]
C
]
D
]7、
A
]
B
]
C
]
D
]8、
A
]
B
]
C
]
D
]9、
A
]
B
]
C
]
D
]10、
A
]
B
]
C
]
D
]
11、
A
]
B
]
C
]
D
]12、
A
]
B
]
C
]
D
]
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.
14.
15.
16.
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)18.(本小题满分12分)19.(本小题满分12分)20.(本小题满分12分)21.(本小题满分12分)22.(本小题满分12分)请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
人教版必修2
第01章
空间几何体
单元卷
参考答案与解析
一、选择题
【答案】
1.C
【解析】圆柱的截面可以是矩形,圆锥的截面可以是三角形,圆台的截面可以是梯形,只有球的截面都是圆,故选C.
考点:几何体的截面图形.
【题型】选择题
【难度】较易
【答案】
2.C
【解析】作出斜边上的高,得到两个小的直
( http: / / www.21cnjy.com )角三角形,一个直角三角形绕斜边所在直线旋转360°
,相当于以两个小直角三角形的直角边所在直线为轴旋转,故将一个直角三角形绕斜边所在直线旋转360°形成的空间几何体是两个同底的圆锥,底面是以直角三角形的斜边上的高为半径的圆面,这两个圆锥的高都在直角三角形的斜边上,且这两个圆锥的高的和等于直角三角形的斜边长.故选
C.
考点:旋转体(圆柱、圆锥、圆台).
【题型】选择题
【难度】较易
【答案】
3.D
【解析】设原棱锥的高为.依题意可得,解得,
所以棱台的高为.故D正确.
考点:棱锥的截面、相似比.
【题型】选择题
【难度】较易
【答案】
4.A
【解析】由题设中的要求可知该几何体的三视图的图形分别是正方形,圆,三角形.
符合条件的只有A,所以选A.
考点:几何体的特征.
【题型】选择题
【难度】较易
【答案】
5.A
【解析】由斜二测画法的规则可知平行性不变,所以①正确,②正确;正方形的直观图是平行四边形,所以③错误;因为平行于轴的线段长度减半,平行于轴的线段长度不变,所以④是错误的,故选A.
考点:斜二测画法.
【题型】选择题
【难度】一般
【答案】
6.A
【解析】由三视图可知该几何体由圆柱挖去一个四棱锥得到,圆柱的底面半径为,高为,棱锥的底面为正方形,边长为,棱锥的高为,∴几何体的体积,故选A.
考点:由三视图求体积.
【题型】选择题
【难度】一般
【答案】
7.D
【解析】直观图的面积,因为,所以实际图形的面积是.
考点:直观图的面积.
【题型】选择题
【难度】一般
【答案】
8.D
【解析】原图如图,表面积为.
( http: / / www.21cnjy.com )
考点:三视图.
【题型】选择题
【难度】一般
【答案】
9.D
【解析】依题意得圆和圆的半径分别为,设圆和圆的圆心与球心的
距离分别为,由球心距与截面圆的半径之间的关系得
,故,故选D.
考点:球的几何性质及运算.
【题型】选择题
【难度】一般
【答案】
10.A
【解析】此几何体为组合体,下部是正方体,上面是球的,并且半径为1,所以此
几何体的体积,故选A.
考点:三视图,几何体的体积.
【题型】选择题
【难度】一般
【答案】
11.B
【解析】要使正方体可以在纸盒内任意转动,则正方体的外接球可以在纸盒内,当球
与正四面体内切时,正方体的棱长最大.设球的半径为,正方体的棱长为,正四
面体底面上的高为,为正四面体一个面的面积,则
,则.所以,则.
考点:四面体的体积,正四面体的内切球.
【题型】选择题
【难度】较难
【答案】
12.A
【解析】由题意可知,正四棱锥底面是由图1中大正方形的四个角拼成的,故图1中的虚线长为图2正四棱锥的底面边长,设为,又正四棱锥的正视图是正三角形,所以正四棱锥的斜高也为,则,即正四棱锥的底面边长为
,易得四棱锥的体积.
考点:锥体的体积公式.
【题型】选择题
【难度】较难
二、填空题
【答案】
13.
【解析】还原直观图为原图形,如图所示,因为,所以,
所以,所以原图形的面积为.
( http: / / www.21cnjy.com )
考点:平面图形的直观图.
【题型】填空题
【难度】较易
【答案】
14.
【解析】从三视图可发现,这是个上面是三棱锥,下面是三棱柱组成体,从俯视图发现,这个几何体是由上面是个正四棱锥,下面是正方体的组合体沿对角线劈了一半,故体积.
考点:三视图求面积和体积.
【题型】填空题
【难度】一般
【答案】
15.
【解析】由题意知折起后原正方形顶点距离最远的两个相差为1,如图中的,折起后原正方形顶点到底面的距离为,如图中的,由图知鸡蛋中心(球心)与蛋巢底面的距离.
( http: / / www.21cnjy.com )
考点:空间几何体.
【题型】填空题
【难度】一般
【答案】
16.
【解析】该几何体的直观图如图所示,侧棱底面,且底面为边长为的正方形,,所以为该几何体外接球的直径,即,的中点为球心,取的中点,则为球心到直线的距离,,所以,解得,所以
,所以外接球的表面积为.
( http: / / www.21cnjy.com )
考点:三视图,球的表面积.
【题型】填空题
【难度】较难
三、解答题
【答案】
17.
表面积,体积为
【解析】由已知易得
.
.
考点:旋转体的表面积和体积.
【题型】解答题
【难度】一般
【答案】
18.
【解析】如图为圆锥轴截面,球心为,可得
设取出球后,水面高为,
因为所以
( http: / / www.21cnjy.com )
考点:圆锥的体积与圆锥的性质.
【题型】解答题
【难度】一般
【答案】
19.
直观图见解析
【解析】步骤是:
①如图(1),以点为原点,水平方向的直线为轴,竖直方向的直线为轴,
过、点分别作轴于点,轴于点;
②如图(2),取任一点,画出相应的轴、轴,使;
③在轴上取,,过、分别作、,且,.
④连接、、并擦去辅助线,
如图(3),则图形即是水平放置图形的直观图.
( http: / / www.21cnjy.com )
考点:平面图形的直观图.
【题型】解答题
【难度】一般
【答案】
20.
(1)(2)
【解析】(1)由三视图知此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.
,,,
所以.
(2)沿点所在母线剪开圆柱侧面,如图,
则,
所以从点到点在侧面上的最短路径的长为.
考点:三视图.
【题型】解答题
【难度】一般
【答案】
21.
(1)俯视图见解析,16
cm2(2)4cm
【解析】(1)该四棱锥的俯视图为边长为4
cm的正方形内含一条对角线,俯视图如图所示,其面积为16
cm2.
( http: / / www.21cnjy.com )
(2)由侧视图可求得.
由正视图可知AD=4且AD⊥PD,
所以在Rt△APD中,cm.
考点:几何体的体积、面积.
【题型】解答题
【难度】一般
【答案】
22.
(1)为中点(2)
【解析】(1)为中点,截面如图所示.
( http: / / www.21cnjy.com )
(2)因为是的中位线,,所以,易得,且,
所以梯形的面积为,
点到截面的距离为到直线的距离,
所以四棱锥的体积,
而四棱锥的体积,
所以四棱锥被截下部分体积,
故上,下两部分体积比.
考点:线面平行性质与判定定理,棱锥体积.
【题型】解答题
【难度】一般
人教版必修2
第01章
空间几何体
单元测试卷
(时间:120分钟 满分:150分)
第Ⅰ卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【题文】截一个几何体,各个截面都是圆面,则这个几何体一定是()
A.圆柱B.圆锥C.球D.圆台
2.【题文】一个直角三角形绕斜边所在直线旋转360°形成的空间几何体为()
A.一个圆锥
B.一个圆锥和一个圆柱
C.两个圆锥
D.一个圆锥和一个圆台
3.【题文】用一个平行于棱锥底面的平面截这个棱锥,截得的棱台上、下底面面积比为,截去的棱锥的高是,则棱台的高是()
A.
B.
C.
D.
4.【题文】中央电视台有一个非常受欢迎的
( http: / / www.21cnjy.com )娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为()
( http: / / www.21cnjy.com )
A.
B.
C.
D.
5.【题文】利用斜二测画法得到的:
①三角形的直观图是三角形;
②平行四边形的直观图是平行四边形;
③正方形的直观图是正方形;
④菱形的直观图是菱形.
以上结论正确的是()
A.①②
B.①
C.③④
D.①②③④
6.【题文】某几何体的三视图如图所示,则该几何体的体积是()
( http: / / www.21cnjy.com )
A.B.C.D.
7.【题文】一个水平放置的平面图形的斜二测直观图是一个底角为,腰和上底均为1的等腰梯形,则这个平面图形的面积为()
A.
B.
C.
D.
8.【题文】如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为()
( http: / / www.21cnjy.com )
A.54
B.162
C.
D.
9.【题文】已知球的半径为2,圆和圆是球的互相垂直的两个截面,圆和圆的面积分别为和,则()
A.1
B.C.2
D.
10.【题文】一个机器零件的三视图如图所示,其中俯视图是一个半圆内切于边长为2的正方形,则该机器零件的体积为(
)
( http: / / www.21cnjy.com )
A.8+B.8+C.8+D.8+
【答案】A
11.【题文】已知一个正四面体纸盒的棱长为,若在该正四面体纸盒内放一个正方体,使正方体可以在纸盒内任意转动,则正方体棱长的最大值为()
A.
B.C.
D.
12.【题文】将一张边长为6
cm的纸片按
( http: / / www.21cnjy.com )如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是()
( http: / / www.21cnjy.com )
A.
B.
C.
D.
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)
13.【题文】如图,正方形的边长为1,它是水平放置的一个平面图形的直观图,则原图形的面积为
.
( http: / / www.21cnjy.com )
14.【题文】某几何体的三视图如图所示(单位:),则该几何体的体积是_____.
( http: / / www.21cnjy.com )
15.【题文】用一个边长为的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为
.
16.【题文】四棱锥的三视图如图所示,四棱锥的五个顶点都在一个球面上,、分别是棱、的中点,直线被球面所截得的线段长为,则该球表面积为
.
( http: / / www.21cnjy.com )
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)
【题文】如图,在四边形中,,,,,,,求四边形绕所在直线旋转一周所成几何体的表面积及体积.
( http: / / www.21cnjy.com )
18.(本小题满分12分)
【题文】设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
19.(本小题满分12分)
【题文】用斜二测画法画出图中水平放置的图形的直观图.
( http: / / www.21cnjy.com )
20.(本小题满分12分)
【题文】已知一个几何体的三视图如图所示.
( http: / / www.21cnjy.com )
(1)求此几何体的表面积;
(2)如果点在正视图中所示位置:为所在线段中点,为顶点,求在几何体表面上,从点到点的最短路径的长.
21.(本小题满分12分)
【题文】已知底面为正方形的四棱锥P-ABC
( http: / / www.21cnjy.com )D如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4
cm的全等的等腰直角三角形.
( http: / / www.21cnjy.com )
(1)根据图(2)所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求PA.
22.(本小题满分12分)
【题文】已知四棱锥中,底面为矩形,底面,,,为的中点.
( http: / / www.21cnjy.com )
(1)在图中作出平面与的交点,并指出点所在位置(不要求给出理由);
(2)求平面将四棱锥分成上下两部分的体积比.
人教版必修2
第01章
空间几何体
单元卷
答题卡
注意事项:
1.
答卷前,考生务必用黑色字迹的钢笔或签字笔将自己姓名和班级填写在答题卡上。
2.
选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案信息号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.
非选择题必须用黑色字
( http: / / www.21cnjy.com )迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。不按以上要求作答的答案无效。
4.
考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。
一、选择题
1、
A
]
B
]
C
]
D
]2、
A
]
B
]
C
]
D
]3、
A
]
B
]
C
]
D
]4、
A
]
B
]
C
]
D
]5、
A
]
B
]
C
]
D
]
6、
A
]
B
]
C
]
D
]7、
A
]
B
]
C
]
D
]8、
A
]
B
]
C
]
D
]9、
A
]
B
]
C
]
D
]10、
A
]
B
]
C
]
D
]
11、
A
]
B
]
C
]
D
]12、
A
]
B
]
C
]
D
]
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)13.
14.
15.
16.
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)18.(本小题满分12分)19.(本小题满分12分)20.(本小题满分12分)21.(本小题满分12分)22.(本小题满分12分)请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效
人教版必修2
第01章
空间几何体
单元卷
参考答案与解析
一、选择题
【答案】
1.C
【解析】圆柱的截面可以是矩形,圆锥的截面可以是三角形,圆台的截面可以是梯形,只有球的截面都是圆,故选C.
考点:几何体的截面图形.
【题型】选择题
【难度】较易
【答案】
2.C
【解析】作出斜边上的高,得到两个小的直
( http: / / www.21cnjy.com )角三角形,一个直角三角形绕斜边所在直线旋转360°
,相当于以两个小直角三角形的直角边所在直线为轴旋转,故将一个直角三角形绕斜边所在直线旋转360°形成的空间几何体是两个同底的圆锥,底面是以直角三角形的斜边上的高为半径的圆面,这两个圆锥的高都在直角三角形的斜边上,且这两个圆锥的高的和等于直角三角形的斜边长.故选
C.
考点:旋转体(圆柱、圆锥、圆台).
【题型】选择题
【难度】较易
【答案】
3.D
【解析】设原棱锥的高为.依题意可得,解得,
所以棱台的高为.故D正确.
考点:棱锥的截面、相似比.
【题型】选择题
【难度】较易
【答案】
4.A
【解析】由题设中的要求可知该几何体的三视图的图形分别是正方形,圆,三角形.
符合条件的只有A,所以选A.
考点:几何体的特征.
【题型】选择题
【难度】较易
【答案】
5.A
【解析】由斜二测画法的规则可知平行性不变,所以①正确,②正确;正方形的直观图是平行四边形,所以③错误;因为平行于轴的线段长度减半,平行于轴的线段长度不变,所以④是错误的,故选A.
考点:斜二测画法.
【题型】选择题
【难度】一般
【答案】
6.A
【解析】由三视图可知该几何体由圆柱挖去一个四棱锥得到,圆柱的底面半径为,高为,棱锥的底面为正方形,边长为,棱锥的高为,∴几何体的体积,故选A.
考点:由三视图求体积.
【题型】选择题
【难度】一般
【答案】
7.D
【解析】直观图的面积,因为,所以实际图形的面积是.
考点:直观图的面积.
【题型】选择题
【难度】一般
【答案】
8.D
【解析】原图如图,表面积为.
( http: / / www.21cnjy.com )
考点:三视图.
【题型】选择题
【难度】一般
【答案】
9.D
【解析】依题意得圆和圆的半径分别为,设圆和圆的圆心与球心的
距离分别为,由球心距与截面圆的半径之间的关系得
,故,故选D.
考点:球的几何性质及运算.
【题型】选择题
【难度】一般
【答案】
10.A
【解析】此几何体为组合体,下部是正方体,上面是球的,并且半径为1,所以此
几何体的体积,故选A.
考点:三视图,几何体的体积.
【题型】选择题
【难度】一般
【答案】
11.B
【解析】要使正方体可以在纸盒内任意转动,则正方体的外接球可以在纸盒内,当球
与正四面体内切时,正方体的棱长最大.设球的半径为,正方体的棱长为,正四
面体底面上的高为,为正四面体一个面的面积,则
,则.所以,则.
考点:四面体的体积,正四面体的内切球.
【题型】选择题
【难度】较难
【答案】
12.A
【解析】由题意可知,正四棱锥底面是由图1中大正方形的四个角拼成的,故图1中的虚线长为图2正四棱锥的底面边长,设为,又正四棱锥的正视图是正三角形,所以正四棱锥的斜高也为,则,即正四棱锥的底面边长为
,易得四棱锥的体积.
考点:锥体的体积公式.
【题型】选择题
【难度】较难
二、填空题
【答案】
13.
【解析】还原直观图为原图形,如图所示,因为,所以,
所以,所以原图形的面积为.
( http: / / www.21cnjy.com )
考点:平面图形的直观图.
【题型】填空题
【难度】较易
【答案】
14.
【解析】从三视图可发现,这是个上面是三棱锥,下面是三棱柱组成体,从俯视图发现,这个几何体是由上面是个正四棱锥,下面是正方体的组合体沿对角线劈了一半,故体积.
考点:三视图求面积和体积.
【题型】填空题
【难度】一般
【答案】
15.
【解析】由题意知折起后原正方形顶点距离最远的两个相差为1,如图中的,折起后原正方形顶点到底面的距离为,如图中的,由图知鸡蛋中心(球心)与蛋巢底面的距离.
( http: / / www.21cnjy.com )
考点:空间几何体.
【题型】填空题
【难度】一般
【答案】
16.
【解析】该几何体的直观图如图所示,侧棱底面,且底面为边长为的正方形,,所以为该几何体外接球的直径,即,的中点为球心,取的中点,则为球心到直线的距离,,所以,解得,所以
,所以外接球的表面积为.
( http: / / www.21cnjy.com )
考点:三视图,球的表面积.
【题型】填空题
【难度】较难
三、解答题
【答案】
17.
表面积,体积为
【解析】由已知易得
.
.
考点:旋转体的表面积和体积.
【题型】解答题
【难度】一般
【答案】
18.
【解析】如图为圆锥轴截面,球心为,可得
设取出球后,水面高为,
因为所以
( http: / / www.21cnjy.com )
考点:圆锥的体积与圆锥的性质.
【题型】解答题
【难度】一般
【答案】
19.
直观图见解析
【解析】步骤是:
①如图(1),以点为原点,水平方向的直线为轴,竖直方向的直线为轴,
过、点分别作轴于点,轴于点;
②如图(2),取任一点,画出相应的轴、轴,使;
③在轴上取,,过、分别作、,且,.
④连接、、并擦去辅助线,
如图(3),则图形即是水平放置图形的直观图.
( http: / / www.21cnjy.com )
考点:平面图形的直观图.
【题型】解答题
【难度】一般
【答案】
20.
(1)(2)
【解析】(1)由三视图知此几何体是一个圆锥加一个圆柱,其表面积是圆锥的侧面积、圆柱的侧面积和圆柱的一个底面积之和.
,,,
所以.
(2)沿点所在母线剪开圆柱侧面,如图,
则,
所以从点到点在侧面上的最短路径的长为.
考点:三视图.
【题型】解答题
【难度】一般
【答案】
21.
(1)俯视图见解析,16
cm2(2)4cm
【解析】(1)该四棱锥的俯视图为边长为4
cm的正方形内含一条对角线,俯视图如图所示,其面积为16
cm2.
( http: / / www.21cnjy.com )
(2)由侧视图可求得.
由正视图可知AD=4且AD⊥PD,
所以在Rt△APD中,cm.
考点:几何体的体积、面积.
【题型】解答题
【难度】一般
【答案】
22.
(1)为中点(2)
【解析】(1)为中点,截面如图所示.
( http: / / www.21cnjy.com )
(2)因为是的中位线,,所以,易得,且,
所以梯形的面积为,
点到截面的距离为到直线的距离,
所以四棱锥的体积,
而四棱锥的体积,
所以四棱锥被截下部分体积,
故上,下两部分体积比.
考点:线面平行性质与判定定理,棱锥体积.
【题型】解答题
【难度】一般
